What geometric principle holds true on the largest scales in a perfectly flat universe?
Answer
The rules of standard Euclidean geometry apply.
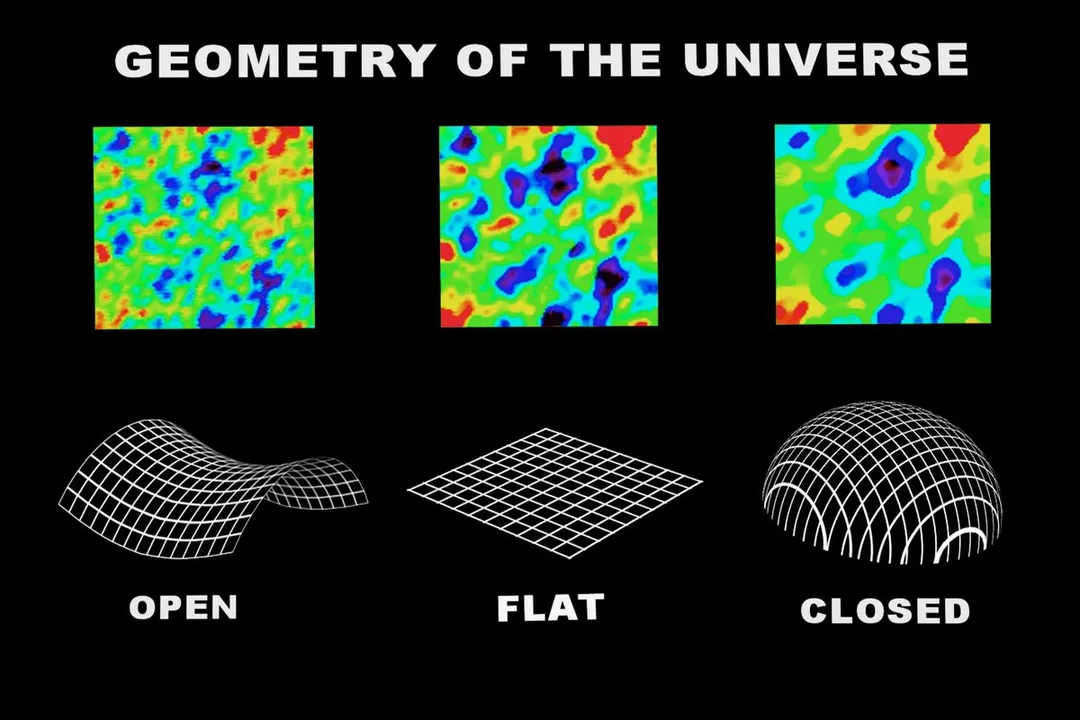
When the universe has zero curvature, meaning $\Omega_0 = 1$, the geometry conforms precisely to Euclidean rules, where parallel lines remain parallel and the angles of a sufficiently large triangle sum exactly to 180 degrees.
Related Questions
How is the large-scale geometry of the universe fundamentally determined?If the density parameter $\Omega_0$ is greater than 1, what type of curvature describes the universe?Which shape best models a universe with negative curvature ($\Omega_0 < 1$)?What geometric principle holds true on the largest scales in a perfectly flat universe?Which specific feature did the WMAP mission primarily map to determine cosmic geometry?In a hypothetical closed universe, how would the sum of angles in a very large triangle formed by light rays compare to a flat universe?Determining the universe's shape relies on mapping echoes from what ancient cosmic event?What is the required value for the density parameter ($\Omega_0$) that corresponds to a perfectly flat universe?What assumption must scientists make about the universe beyond the observable horizon to conclude the *entire* cosmos is flat based on local measurements?According to the summary table, what is the simplified fate implied by a flat universe ($\Omega_0 = 1$)?