What is the shape of the universe according to NASA?
The question of how to describe the overall shape of the cosmos has occupied scientists and thinkers for centuries, but modern cosmology, heavily informed by NASA missions, has narrowed the possibilities down to three primary geometric outcomes. Whether the universe is shaped like a giant sphere, an infinitely expanding saddle, or a perfectly flat plane dictates how light travels across vast distances and profoundly influences its ultimate fate. Determining this shape relies on measuring the universe's curvature, a feat achieved not by direct observation of the edges, but by precisely mapping the echoes of the Big Bang itself.
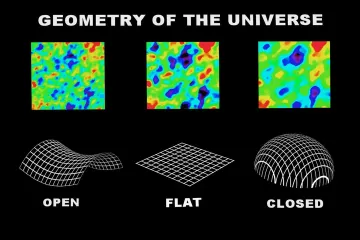
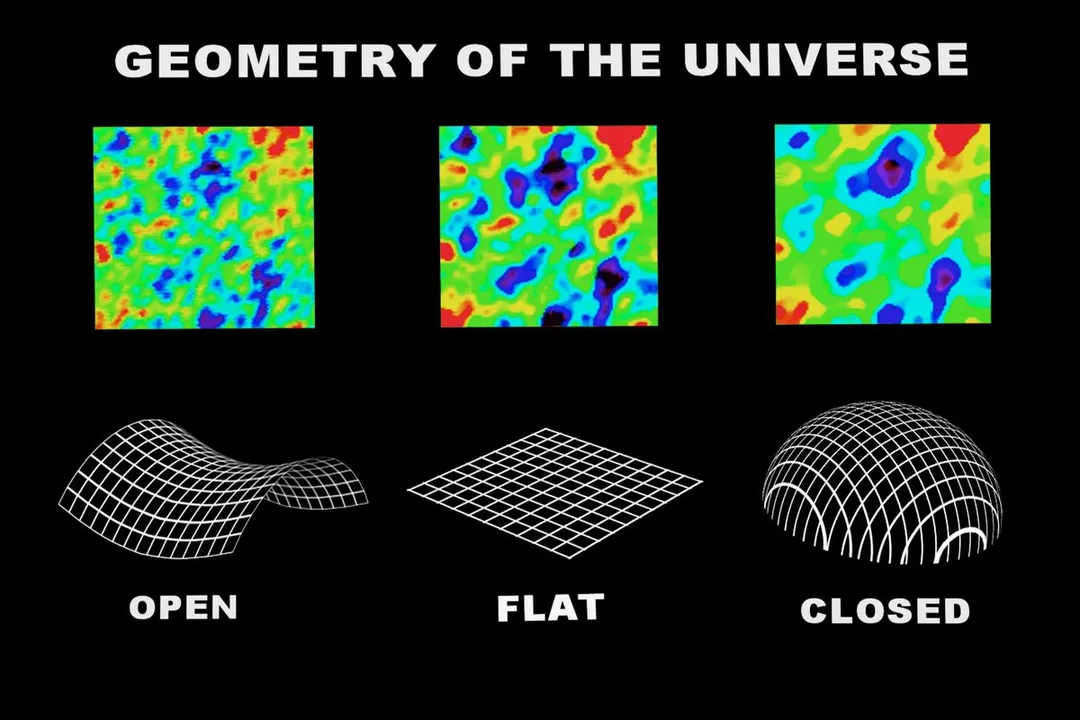
# Cosmic Geometry

The geometry of the universe is fundamentally tied to its average density. Cosmologists use the parameter (Omega naught) to compare the actual average mass-energy density of the universe against a specific critical density required to perfectly balance expansion. This comparison dictates one of three possible large-scale structures.
First, if the actual density is greater than the critical density (), the universe has positive curvature. Think of this as a hypersphere—a three-dimensional surface curved back upon itself, much like the surface of a standard ball, only in higher dimensions. In such a closed universe, if you travel far enough in a straight line, you would eventually return to your starting point. Parallel lines, such as those drawn on the surface of a sphere, would eventually converge.
Second, if the actual density is less than the critical density (), the universe possesses negative curvature. This geometry is analogous to a saddle shape, often called an open universe. In this scenario, the universe is infinite, and parallel lines diverge, spreading farther apart as they extend into space.
The third, and perhaps most elegant, possibility is that the universe is perfectly flat (). A flat universe does not curve in any direction, meaning the rules of standard Euclidean geometry—the geometry we learn in school—hold true on the largest scales. In a flat universe, parallel lines remain perpetually parallel.
# WMAP Measurements

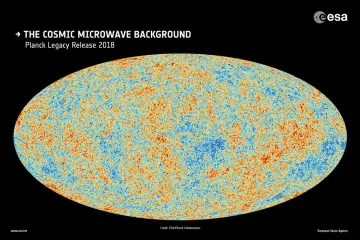
The most significant data pointing toward the current consensus comes from NASA's Wilkinson Microwave Anisotropy Probe (WMAP) mission. WMAP was designed to map the Cosmic Microwave Background (CMB), the faint afterglow radiation left over from when the universe was only about 380,000 years old. The patterns of temperature fluctuations—the tiny hot and cold spots in the CMB—act as a cosmic yardstick. By measuring the apparent size of these spots, scientists can infer the geometry through which the light traveled to reach us.
The WMAP results, analyzed by scientists including those at NASA's Goddard Space Flight Center, strongly indicated that the universe is extremely close to being flat. The data suggested the density parameter is very near to $1$. Later analysis, building upon WMAP's legacy and incorporating other data, confirms this extremely flat geometry with high precision.
It is important to note that while WMAP provided crucial early evidence, its measurements are refined over time. Data from successor experiments, like the European Space Agency's Planck satellite, have further confirmed the WMAP findings, showing the universe is flat within a very small margin of error.
# Density Relation

Understanding why being equal to $1$ implies flatness requires grasping the concept of the critical density. This critical value is the precise amount of mass and energy needed to stop the universe's expansion exactly at the moment it would otherwise begin to collapse back in on itself (in a closed scenario) or to slow its expansion asymptotically (in a flat scenario).
If the universe contained more matter and energy than this critical amount, gravity would win, leading to a closed geometry. If it contained less, the expansion would continue forever, resulting in an open geometry. The fact that WMAP measured the density to be so close to the critical value—effectively —is a remarkable finding. To put this precision into perspective, imagine measuring the curvature of the Earth's surface. If the Earth were slightly curved, you might notice it over a few hundred miles. However, to measure the universe as flat across billions of light-years requires measuring the density parameter to be within a few percentage points of $1$. This means that if the universe were curved, that curvature is so slight that it would only become apparent over distances much greater than the entire observable horizon.
# Observable Limits
A crucial distinction must be made between the observable universe and the entire universe. Because the universe has a finite age—about 13.8 billion years—light has only had that much time to travel to us. This sets a boundary, the cosmic horizon, beyond which we cannot see. All the data we possess, including the WMAP measurements, relate only to the geometry within our observable bubble.
The observable universe appears to be perfectly flat. This observation is the foundation of the scientific conclusion, but it requires an assumption. Scientists generally assume that the universe is homogeneous and isotropic—meaning it looks the same everywhere and in every direction—on the largest scales. If this principle holds true beyond our visible horizon, then the geometry we measure locally (flatness) should describe the shape of the entire cosmos. If the universe were, for example, a small, closed sphere, we might not have traveled far enough yet to detect its curvature, but the assumption of large-scale uniformity strongly favors the observed flatness extending outwards indefinitely.
This reliance on the cosmological principle—that the universe is fundamentally uniform—is an act of faith, albeit a highly successful one in physics. We cannot physically look beyond the horizon to check.
# Implications Flatness
The finding that the universe is flat has profound conceptual consequences for how we model reality. In a flat geometry, the principles of Euclidean geometry apply across the largest scales. For instance, the angles of a very large triangle drawn with light rays from distant galaxies would sum precisely to $180$ degrees.
Consider a local region of space. If you drew a perfect triangle using three extremely distant, isolated galaxies, the sum of the angles between the light paths connecting them would equal . Contrast this with a hypothetical, closed universe where the angles would sum to more than , or an open universe where they would sum to less than .
The fact that we live in a universe where the "straightest possible line"—a geodesic—appears to be straight rather than curving inward or outward is significant. While we know that gravity bends light paths locally around massive objects like stars and galaxies, this local bending does not reflect the overall background geometry of space-time itself. If the universe were globally closed, even if we only saw a small region, the overall warping would mean that geometry would eventually betray itself over truly immense scales.
The near-perfect flatness suggests an extraordinary history for the early universe. According to inflationary theory, a period of rapid, exponential expansion moments after the Big Bang would have smoothed out any initial curvature, much like blowing up a wrinkled balloon causes the surface area immediately around you to appear flatter. The current measurement is so precise that it places very strict constraints on how much inflation must have occurred.
# Data Presentation
To better illustrate the relationship between density and shape, one can summarize the established cosmological parameters based on WMAP and subsequent data:
| Geometric Shape | Curvature | Density Parameter () | Fate Implied (Simplified) |
|---|---|---|---|
| Closed | Positive | Eventually re-collapses | |
| Flat | Zero | Expands forever, slowing asymptotically | |
| Open | Negative | Expands forever, never slowing completely | |
| [2][6] |
The observed data places the measured very close to $1$. This means that the total energy density—including dark matter, ordinary matter, and dark energy—is what is required to create a universe that expands forever but slows its rate of expansion over infinite time, rather than collapsing.
If we were to devise a thought experiment to test this, imagine establishing two perfectly parallel laser beams fired from two different galaxies, separated by billions of light-years. In our current, flat model, these beams would never intersect or drift apart from each other relative to the space between them. If, however, the universe possessed a slight positive curvature that we simply haven't seen the effects of yet, those beams would eventually cross paths far in the distant future, effectively closing the loop. The WMAP evidence suggests that such a crossing point lies far beyond the observable cosmos, if it exists at all. The current precision essentially limits any such hypothetical curvature to scales we cannot probe with current technology.
The shape conclusion thus rests on the extremely successful verification of the CDM concordance model, which successfully incorporates dark energy () and cold dark matter (CDM) alongside the observed geometry. The universe's geometry is a direct, measurable output of this model, making the WMAP results a cornerstone of modern astrophysics.
Related Questions
#Citations
What is the shape of the universe? - StarChild - NASA
Shape of the universe - Imagine the Universe! - NASA
WMAP Overview
What is the shape of the universe?
NASA's website states the shape of the universe proven to ...
Shape of the universe
What shape is the universe?
Galaxy Basics
What is the shape of the universe?