What is the true shape of the universe?

The question of what shape the cosmos takes is one of the deepest inquiries in cosmology, fundamentally tied to how much "stuff"—matter and energy—exists within the expanse of space. This shape isn't a visual contour like that of a marble or a balloon, but rather a description of the overall geometry that governs the paths of light and matter across the largest scales. ^[2]^[4] This geometry is determined by the universe's overall density, which dictates whether the curvature of spacetime is positive, negative, or precisely zero. ^[5]

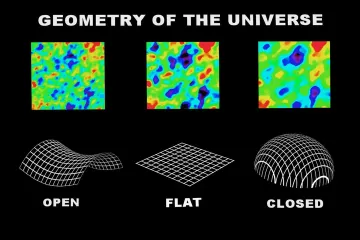
Cosmologists use the density parameter, denoted as $\Omega$ (Omega), to classify these possibilities. ^[5] This parameter compares the actual average energy density of the universe to a specific value called the critical density ( $\Omega_0$ ) required to exactly balance expansion. ^[5] If the actual density is greater than this critical density, the universe possesses positive curvature, resulting in a closed geometry, similar to the surface of a sphere. ^[2]^[5] Conversely, if the actual density falls short of the critical density, the universe has negative curvature, leading to an open geometry, which can be conceptually visualized like the surface of a saddle. ^[5] The third option, a flat universe, occurs when the actual density matches the critical density exactly, meaning $\Omega$ equals one. ^[2]^[5]

# Cosmic Geometry

The geometry dictates basic rules of spatial measurement. In a positively curved (closed) space, if you drew two parallel lines, they would eventually meet, much like lines of longitude converge at the poles of the Earth. ^[5] Furthermore, the sum of the interior angles of a triangle drawn in such a space would always be greater than 180 degrees. ^[5]

For a negatively curved (open) universe, parallel lines diverge from one another, spreading apart as they extend. ^[5] Any triangle drawn within this space would have interior angles that sum to less than 180 degrees. ^[5]

The flat universe, where $\Omega = 1$ , represents the intermediate case. Here, the geometry adheres to standard Euclidean rules: parallel lines stay equidistant, and the angles of a triangle add up perfectly to 180 degrees. ^[5] If the universe is perfectly flat, it is generally assumed to extend infinitely in all directions. ^[2]

We can summarize these geometric possibilities based on the density parameter:

Geometry	Curvature	Density Parameter ( $\Omega$ )	Triangle Angle Sum	Visualization
Closed	Positive	$\Omega > 1$	$> 180^\circ$	Sphere Surface
Flat	Zero	$\Omega = 1$	$= 180^\circ$	Euclidean Plane
Open	Negative	$\Omega < 1$	$< 180^\circ$	Saddle Surface

^[2]^[5]

# Density Parameter

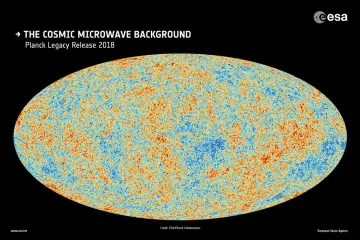
The main way scientists probe the universe’s shape is by measuring its density via the Cosmic Microwave Background (CMB) radiation—the faint echo of the Big Bang. ^[6] Data gathered from missions like the Planck satellite have provided extremely precise measurements of this relic radiation. ^[6] By analyzing the patterns and size of the temperature fluctuations (hot and cold spots) imprinted on the CMB, researchers can deduce the geometry of the space through which that radiation traveled. ^[4]^[6]

The consensus emerging from these high-precision measurements strongly points toward a universe that is flat. ^[2]^[4]^[6] The Planck mission results indicate that the total energy density of the universe is very, very close to the critical density, with $\Omega_0$ being measured at a value incredibly close to $1.0$. ^[6] The current uncertainty in this measurement is so small that the universe appears geometrically flat to within a fraction of a percent. ^[2]^[4] This near-perfect flatness is one of the most significant findings in modern cosmology, reinforcing the standard model of cosmic inflation which predicts this outcome. ^[6]

When we consider the implications of this flatness, we must appreciate the level of precision involved. If the universe were actually closed, it would have to be vastly larger than the region we can observe for it to appear flat to us now. ^[4] Imagine standing on the surface of an enormous beach ball; from your perspective, the local ground looks perfectly flat, but that flatness is only an illusion caused by your small vantage point relative to the ball's massive radius. ^[4] The data suggest that if the universe is curved, its radius of curvature must be so vast—likely thousands of times larger than the observable universe—that our measurements register it as zero curvature. ^[1]^[4] It is an understatement to say the universe is flat; it means its overall geometry is almost indistinguishable from Euclidean geometry within our observational horizon. In practical terms, if we fired two lasers perfectly parallel from opposite ends of the observable cosmos, they would almost certainly arrive at their destination parallel, never converging or diverging noticeably. ^[5]

# Topology Matters

It is essential to distinguish between geometry (curvature) and topology (connectivity). ^[2]^[7] Geometry describes the local rules of space (flat, open, or closed), while topology describes the global structure—how the space fits together, like wrapping a sheet of paper into a cylinder or a torus. ^[2]^[7]

A geometrically flat universe does not automatically mean it is infinitely large; it could be finite but unbounded if its topology is closed in a non-obvious way. ^[2] For instance, a flat universe could be topologically equivalent to a three-dimensional torus, often described as a doughnut shape. ^[2]^[7] In a toroidal topology, if you travel far enough in one direction, you would eventually loop back to your starting point, much like characters in classic video games reappearing on the opposite side of the screen. ^[7]

The search for repeating patterns in the sky is a direct test for these multi-connected topologies. ^[2] If the universe were a torus with a circumference smaller than the distance light has traveled since the Big Bang, we should theoretically see duplicate images of the same distant galaxies or repeating patterns in the CMB. ^[7] Current analyses, however, have found no statistical evidence for such repeating patterns across the entire sky. ^[1]^[7] This suggests that if the universe is indeed flat, its topology is likely that of an infinite, non-looping space, though the possibility of a finite universe larger than our observable horizon remains open. ^[2]^[7]

One interesting analytical consideration arises when comparing the geometric flatness constraint with the topological search results. The CMB observations limit the radius of curvature to be greater than about 412 times the observable universe's radius. ^[1] If the universe were a flat torus, its fundamental domain (the smallest repeating unit) would have to be larger than this limit to avoid generating detectable echoes in the CMB data. ^[1] This sets a very high bar for any complex, finite topology. While the geometry is almost certainly flat based on density, proving the simple, infinite topology requires confirming the absence of repeating patterns, which is always subject to the limitations of our observational volume.

# Observable Limits

The concept of the observable universe imposes a crucial limitation on our knowledge of the true shape. ^[4] We can only observe objects whose light has had time to reach us since the Big Bang, defining a sphere of influence roughly $93$ billion light-years in diameter, known as the Hubble sphere. ^[4]

Whether the entire universe is finite or infinite depends on its true global topology and its overall geometric flatness. ^[2] If the universe is perfectly flat and infinite, we will never see the whole thing, and our local measurements will always reflect flatness. ^[5] If it is closed, we will only ever see a fraction of the sphere, again appearing flat unless we travel far enough to start seeing light wrap around. ^[2]

The constraint on $\Omega_0 \approx 1$ is an incredibly tight measurement of the local curvature. ^[6] It suggests that the large-scale structure of space, within the bounds of what we can currently measure, is indeed flat. ^[4] Any deviation from flatness must occur on scales far larger than the observable universe itself, rendering it undetectable for now. ^[4] For general readers, this translates to an important practical point: for virtually any cosmological process happening now or in the recent past, treating space as flat (Euclidean) provides an accurate enough description for most calculations. ^[5] The differences only become relevant when considering travel times spanning billions of years or the entire age of the universe.

# Future Searches

While the evidence strongly supports a flat geometry, future observations aim to tighten the constraints even further. Pinpointing the value of $\Omega$ with even greater accuracy will help solidify our confidence in the standard cosmological model. ^[6] If future, higher-resolution CMB experiments or large-scale galaxy surveys detect a slight, consistent deviation from $\Omega = 1$ , it would signal a return to the closed or open possibilities, potentially requiring a rethinking of the inflation theories that predicted flatness. ^[4] Similarly, continued efforts to find repeating structures in galaxy distributions or the CMB could rule out complex finite topologies, strengthening the case for an infinitely extending flat space. ^[7] For now, the current state of astronomical knowledge paints a picture of a geometrically flat cosmos, vast enough that its edges—if they exist at all—lie far outside the reach of our most powerful telescopes. ^[1]^[2]