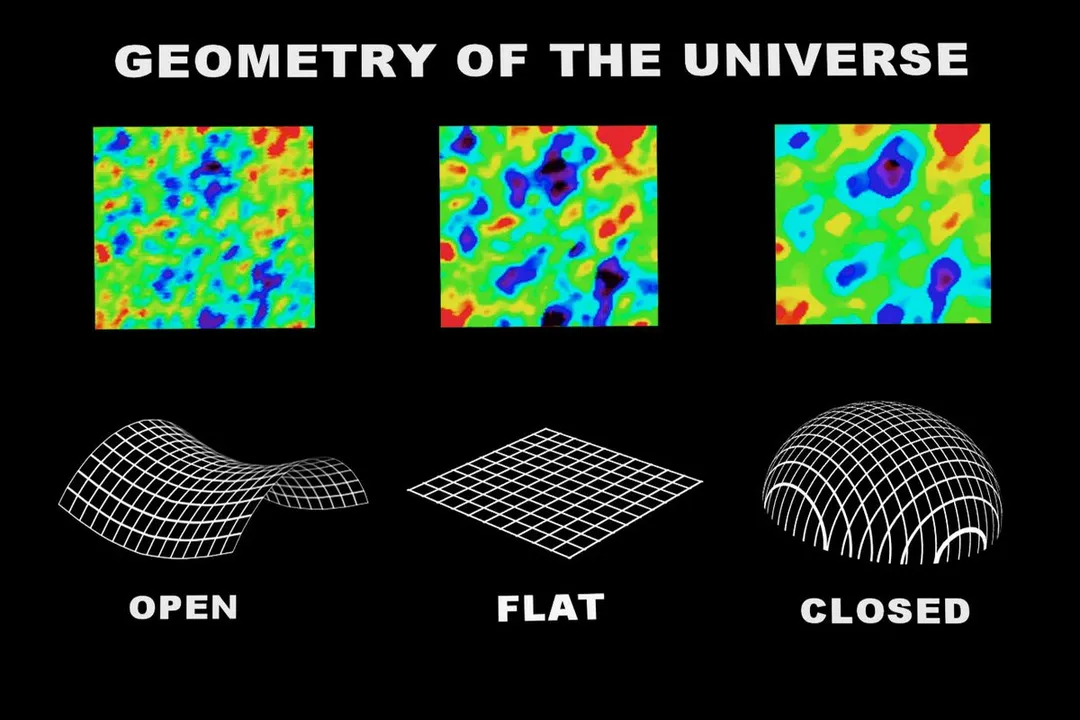
In a closed geometry, what happens to two parallel lines drawn across space?
Answer
They would eventually meet
A closed geometry has positive curvature, similar to a sphere's surface. In such a space, parallel lines, like lines of longitude, will converge.
Related Questions
What fundamental property dictates the overall geometry (shape) of the cosmos?What is the density parameter, $\Omega$, compared against to classify cosmic geometry?In a closed geometry, what happens to two parallel lines drawn across space?If the universe has negative curvature, what is the resulting geometry classification?What condition results in a flat universe where $\Omega$ equals one?What geometric rule applies to a triangle drawn in a negatively curved universe?How do scientists primarily obtain precise measurements of the universe's density to determine its shape?What is the key distinction between geometry and topology in cosmology?If the universe is geometrically flat ($\Omega=1$), what topological structure could make it finite but unbounded?What observational evidence would suggest a finite, multi-connected topology like a torus?If the universe appears locally flat, what must be true about its radius of curvature if it is curved?