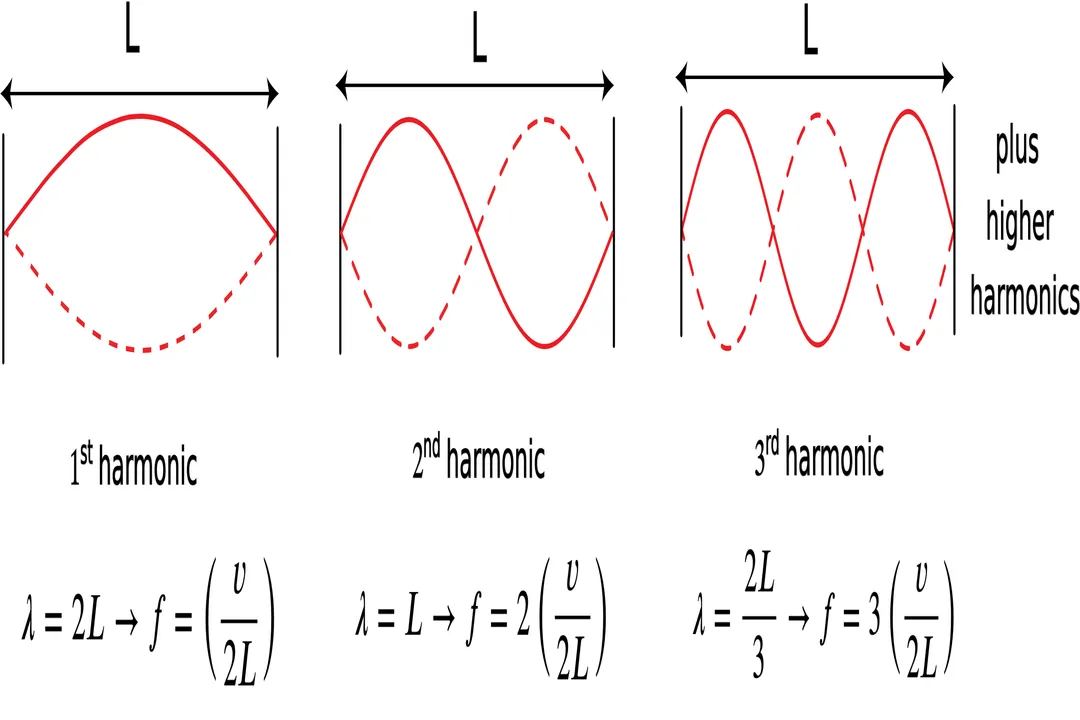
In a system fixed at one end and free at the other (Fixed-Free), what constraint does the length $L$ place on the allowed wavelengths?
Answer
L must accommodate an odd number of quarter-wavelengths
Because one end is a node and the other is an antinode (for displacement waves), the length $L$ must contain $n$ segments of a quarter wavelength, where $n$ can only be 1, 3, 5, etc.
Related Questions
What type of phenomenon fundamentally characterizes a standing wave?When a pulse traveling down a rope hits a tightly secured (fixed) end, what occurs upon reflection?What principle dictates how the incident and reflected waves combine at any given point in the medium?What is the mathematical signature distinguishing a standing wave $y(x, t)$ in a one-dimensional system?What defines the locations known as nodes on a standing wave?What is the precise distance separating any two adjacent nodes in a standing wave pattern?For a system fixed at both ends (Fixed-Fixed), what condition must the length $L$ satisfy to establish a standing wave?In a system fixed at one end and free at the other (Fixed-Free), what constraint does the length $L$ place on the allowed wavelengths?What concept describes the situation where the reflected wave's amplitude is less than the incident wave's amplitude in reality?For longitudinal sound waves in an air pipe, what condition characterizes a closed end?