How do standing waves form?

The peculiar phenomenon of a wave that seems frozen in place, oscillating yet not traveling, is a common yet fascinating subject in physics: the standing wave. To truly grasp how these stationary patterns emerge, we must move beyond thinking of a wave as a simple ripple moving from point A to point B. Instead, we must visualize the interaction—the collision and combination—of waves traveling in contrary directions within a confined space.

At its heart, a standing wave is an interference phenomenon, not a traveling wave itself. It arises when two waves, possessing the exact same frequency and amplitude, propagate through the same medium but move in opposite directions. This meeting point is where the magic happens, governed by the principle of superposition.

# Wave Collision

Imagine sending a single pulse down a rope that is tightly secured at one end, like a spring or a large Slinky. The pulse travels from your hand to the fixed boundary. When that pulse hits the fixed end, it doesn't simply stop; it reflects and returns back along the rope, but with an inversion—an upward pulse becomes a downward pulse.

Now, consider not just one pulse, but a continuous wave—a constant stream of crests and troughs. As the initial, or incident, wave travels towards the boundary, the reflected wave travels away from it, heading back toward the source. Because both waves originated from the same source, they share the same frequency and speed, meaning they also share the same wavelength ($\lambda \backslash lambda$).

When these two waves, identical in form but opposite in direction, overlap, the medium at any given point experiences the combined effect of both displacements, as dictated by the principle of superposition. If a crest from the incident wave meets a trough from the reflected wave, they cancel out—this is destructive interference. If two crests meet, they add up to create a larger crest—constructive interference.

# Stationary Pattern

If the timing is just right—a condition we will explore shortly—this interference pattern becomes fixed in space and time, giving the standing wave its name. At any specific location along the medium, the net displacement of the material will either always be zero, or it will oscillate with the full amplitude of the original waves.

The resulting combined wave is mathematically described by separating the spatial dependence (where the wave is) from the time dependence (how it moves). For a one-dimensional system, like a string fixed at both ends, the resulting displacement $y(x,t)y(x,\; t)$ often takes a form where the spatial part dictates the maximum possible oscillation at that point, and the time part dictates how that maximum oscillation occurs over time, for example:

$$y(x,t)=2A\cos \left(\frac{2\pi x}{\lambda }\right)\cos (\omega t)y(x,\; t)\; =\; 2A\; \backslash cos\backslash left(\backslash frac\{2\backslash pi\; x\}\{\backslash lambda\}\backslash right)\; \backslash cos(\backslash omega\; t)$$

Notice how the term containing $xx$ (the position along the string) is independent of time, and the term containing $tt$ (time) is independent of position. This separation is the mathematical signature of a standing wave: the shape defined by $xx$ remains stationary, while the amplitude defined by $tt$ oscillates.

# Points of Stillness

The fixed locations that arise from this persistent interference define the structure of the standing wave, categorized into two primary features:

# Nodes and Antinodes

The points that never move are called nodes. These are the locations where the incident and reflected waves are always perfectly out of phase, resulting in complete destructive interference regardless of the moment in time. In a string fixed at both ends, these nodes must occur at the physical ends of the string. The distance between any two adjacent nodes is precisely half a wavelength ($\lambda \mathrm{/}2\backslash lambda/2$).

Conversely, the points where the oscillation is maximal are called antinodes. Here, the incident and reflected waves always arrive in phase, producing constructive interference that doubles the amplitude of the original traveling waves. Antinodes are located exactly halfway between two adjacent nodes.

The presence of nodes and antinodes means that while the string (or air column, or whatever the medium is) is vibrating, certain specific locations are momentarily or permanently stationary. This is why the wave appears standing—the energy transfer that characterizes a true traveling wave is, on average, zero in a pure standing wave.

# Boundary Conditions and Resonance

A standing wave pattern can only establish itself if the geometry of the medium allows the reflection process to sustain the required pattern of nodes and antinodes. This requirement is known as resonance, and it drastically restricts the possible wavelengths and, consequently, the possible frequencies that can form a stable pattern.

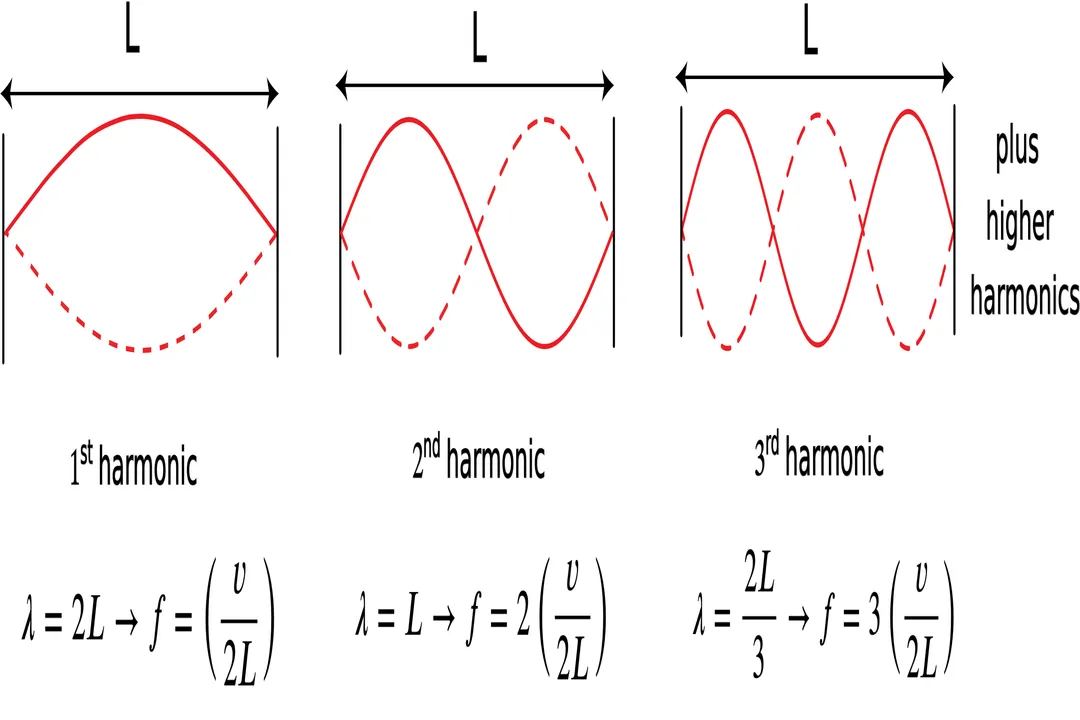
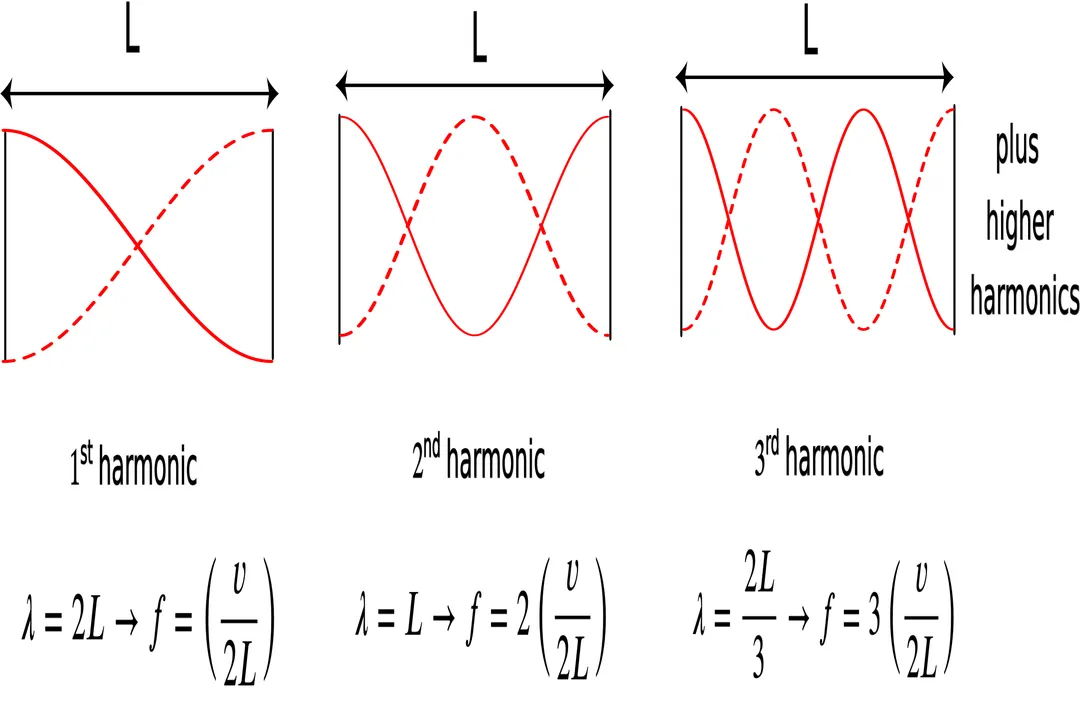
# Fixed-Fixed Systems

The most straightforward example involves a medium fixed at both ends, such as a guitar string fixed at the bridge and the nut, or a uniform tube sealed at both ends (for displacement waves). Since the ends must be stationary, they must both function as nodes.

For this configuration to work, the length of the medium, $LL$, must perfectly accommodate an integer number of half-wavelengths. If $nn$ represents the harmonic number ($n=1,2,3,\dots n=1,\; 2,\; 3,\; \backslash dots$):

$${\lambda }_n=\frac{2L}{n}\backslash lambda\_n\; =\; \backslash frac\{2L\}\{n\}$$

This means the fundamental mode ($n=1n=1$) fits exactly one half-wavelength across the length $LL$ (${\lambda }_1=2L\backslash lambda\_1\; =\; 2L$). The second harmonic ($n=2n=2$) fits a full wavelength (${\lambda }_2=L\backslash lambda\_2\; =\; L$), and so on. Each of these specific wavelengths corresponds to a specific, allowed frequency, $f_{n}f\_n$, determined by the wave speed $vv$ in the medium: $f_n=v\mathrm{/}{\lambda }_n=n(v\mathrm{/}2L)f\_n\; =\; v/\backslash lambda\_n\; =\; n(v/2L)$.

# Comparing Wavelength Restrictions

The key takeaway here is that for traveling waves, the frequency is usually set by the source, and the speed (determined by the medium) sets the wavelength. However, in the context of standing waves, the physical boundary L dictates the allowed wavelengths, which in turn determine the discrete set of frequencies that can resonate and create a stable pattern. This is a crucial inversion of common wave intuition. If you pluck a string, only the frequencies matching these allowed ${\lambda }_n\backslash lambda\_n$ values will create a sustained, visible standing pattern; all others will result in a non-repeating, messy superposition that quickly damps out.

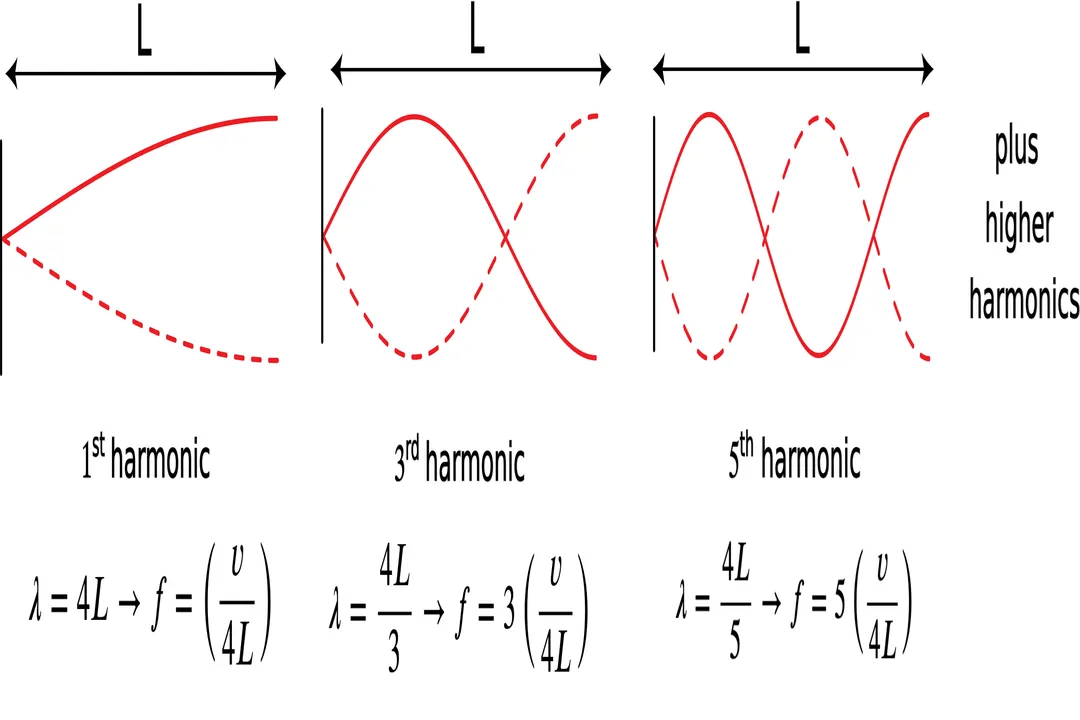
# Fixed-Free or Open-Closed Systems

The boundary conditions drastically change the allowed wavelengths, which is vital for understanding instruments like clarinets or bottles. Consider a string fixed at one end (a node) and attached to a freely moving ring at the other (an antinode for displacement waves).

In this case, the length $LL$ must accommodate an odd number of quarter-wavelengths:

$${\lambda }_n=\frac{4L}{n}\text{where }n=1,3,5,\dots \backslash lambda\_n\; =\; \backslash frac\{4L\}\{n\}\; \backslash quad\; \backslash text\{where\; \}\; n\; =\; 1,\; 3,\; 5,\; \backslash dots$$

The fundamental mode ($n=1n=1$) fits exactly one quarter-wavelength (${\lambda }_1=4L\backslash lambda\_1\; =\; 4L$), resulting in a node at one end and an antinode at the other. Higher harmonics only allow odd multiples of this quarter-wavelength. This restricted set of frequencies means that a fixed-fixed system and a fixed-free system, even of the same length and medium, will have entirely different sets of resonant notes. For example, the fixed-fixed system has frequencies at $f_1,2f_1,3f_1,\dots f\_1,\; 2f\_1,\; 3f\_1,\; \backslash dots$, while the fixed-free system has frequencies at f'_1, 3f'_1, 5f'_1, \dots, where f'_1 is its own fundamental frequency based on $4L4L$.

# Transverse Versus Longitudinal Boundaries

The physical interpretation of nodes and antinodes must be carefully matched to the type of wave being observed, especially when moving from mechanical waves on strings (transverse) to sound waves in air columns (longitudinal).

On a string (transverse displacement wave):

• A fixed end (tied down) is a displacement node (no movement).
• A free end (allowed to move up/down) is a displacement antinode (maximum movement).

For sound in a pipe (longitudinal pressure wave):

• A closed end (like a physical wall) restricts air molecule movement, leading to maximum pressure variation, which is a pressure antinode (and a displacement node).
• An open end (exposed to the atmosphere) has pressure fixed near atmospheric pressure, resulting in a pressure node (and a displacement antinode).

It is easy to confuse these conventions. For instance, an open organ pipe, open at both ends, behaves like a string with two free ends regarding displacement, but regarding pressure, it has nodes at both ends, making it mathematically analogous to the fixed-fixed string. This is a common point of confusion; understanding the physical constraint at the boundary—whether it restricts motion or pressure—is what dictates the mathematical condition.

# Beyond Simple Confinement: The Imperfect Reality

While pure standing waves arise from perfectly matched, reflected waves, reality often involves some degree of imperfection. This introduces a practical concept known as the Standing Wave Ratio (SWR).

When the reflected wave's amplitude is slightly less than the incident wave's amplitude—due to energy lost through damping, transmission through the boundary, or imperfect reflection—the resulting wave is not purely stationary.

This leads to an interesting analysis:

If the incident and reflected waves are of unequal amplitude, the points that were perfect nodes ($y=0y=0$) will only exhibit a minimum displacement, not zero displacement. The resulting wave pattern is a superposition of a standing wave and a small traveling wave component. If the SWR is high (large difference between maximum and minimum amplitude), the wave looks mostly stationary. If the SWR approaches 1, it means the reflection is almost nonexistent, and the wave acts almost entirely like a traveling wave. This traveling component is precisely what carries away the energy supplied by the source over long distances, as a pure standing wave, by definition, transfers no net energy.

This explains why, in the real world, you must continuously feed energy into a system (like plucking a guitar string) to maintain the standing wave pattern; the slight traveling component ensures the energy eventually leaks out or is dissipated as heat.

# Higher Dimensions

The principles are not limited to one dimension like a string or a pipe. Standing waves can form in two-dimensional surfaces, such as the membrane of a drum, resulting in complex, beautiful patterns known as Chladni figures.

In these 2D cases, the nodes are no longer points but instead become nodal lines—lines across the surface where no movement occurs. The spatial variation of the displacement must satisfy the boundary conditions (zero displacement) across the entire rectangular perimeter simultaneously. This imposes two sets of constraints: one for the $xx$-direction and one for the $yy$-direction, each governed by its own integer harmonic numbers ($nn$ and $mm$). The resulting frequency depends on both integers and the dimensions of the rectangle ($\omega \propto \sqrt{(n\mathrm{/}{L}_x{)}^2+(m\mathrm{/}{L}_y{)}^2}\backslash omega\; \backslash propto\; \backslash sqrt\{(n/L\_x)^2\; +\; (m/L\_y)^2\}$). This is why striking a cymbal or drumhead produces a complex chord of sound; multiple $(n,m)(n,\; m)$ combinations resonate at frequencies that are often in simple ratios, creating the instrument's timbre.

Standing waves also appear in non-mechanical systems, illustrating the universality of wave interference. In optics, lasers rely on standing light waves created between two mirrors (an optical cavity). In these cases, the wavelength is microscopic (nanometers), and the standing pattern is established by the highly reflective nature of the mirrors. Similarly, X-ray beams interfering with diffracted beams can create X-ray Standing Waves (XSW) used to probe atomic positions on material surfaces, demonstrating that the concept applies whenever any form of energy propagates as a wave, whether it’s transverse displacement, longitudinal pressure, or electromagnetic fields.

Whether it's the resonant hum of an instrument, the pattern on a vibrating drum, or the standing patterns in an electrical transmission line due to an impedance mismatch, the formation of a standing wave always relies on the same foundational recipe: the perfect, phased interaction of a wave and its reflection, constrained by the boundaries of its environment.