What causes wave–particle duality?
The perplexing nature of wave–particle duality sits at the very foundation of our modern understanding of the physical world, suggesting that the objects we once categorized neatly as either waves (like light or sound) or particles (like billiard balls) defy such simple classification. It is not that an electron or a photon is sometimes a wave and sometimes a particle; rather, it possesses an intrinsic nature that manifests differently depending on how we choose to measure or observe it. The question isn't what switches the object from one state to another, but rather what deep feature of reality mandates this dual description in the first place.
# Historical Roots
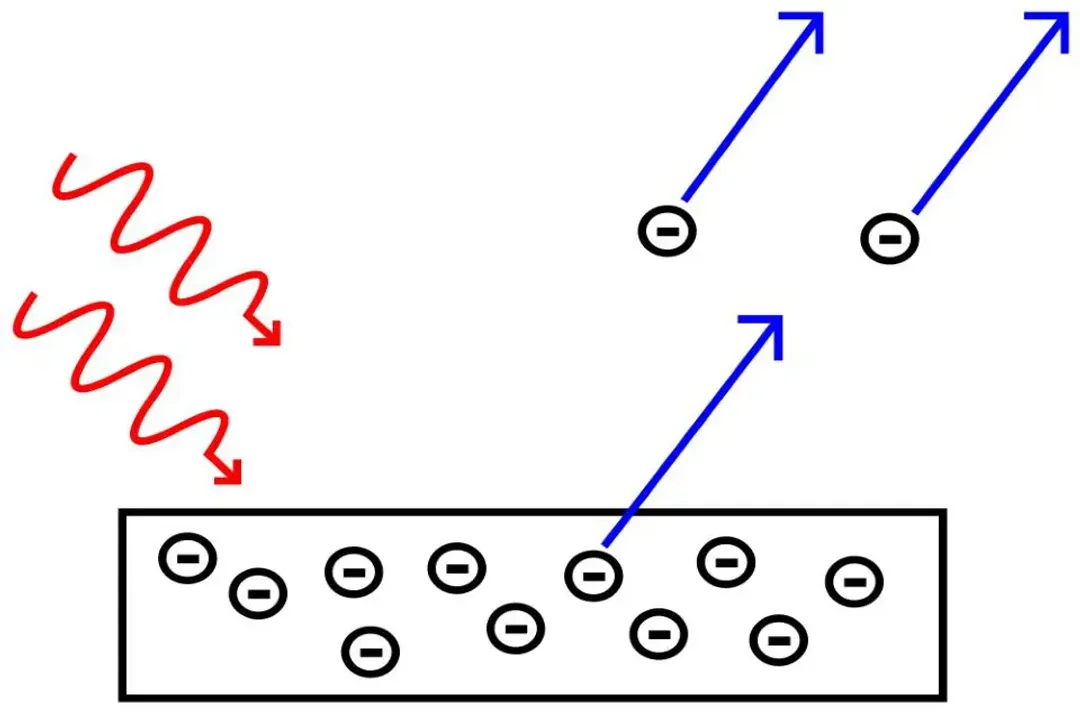
The seeds of this profound shift in perspective were sown in the early twentieth century as physicists grappled with experimental results that classical physics simply could not explain. Light, long understood through the work of Maxwell as a propagating wave phenomenon, exhibited particle-like behavior during the photoelectric effect, where energy transfer seemed to happen in discrete packets, or quanta, later called photons. This was a necessary contradiction: light had to be both to account for all observed phenomena.
A significant leap forward came with Louis de Broglie's hypothesis, which boldly proposed that if light waves could behave like particles, then particles of matter—like electrons—must also possess wave-like properties. This was formalized by the de Broglie relation, which connects the momentum () of a particle to an associated wavelength () through Planck’s constant (): . The constant is the crucial link, anchoring the wave characteristic to the particle's momentum. If were zero, the wave aspect would vanish entirely, and everything would conform perfectly to classical mechanics.
# Experimental Proof

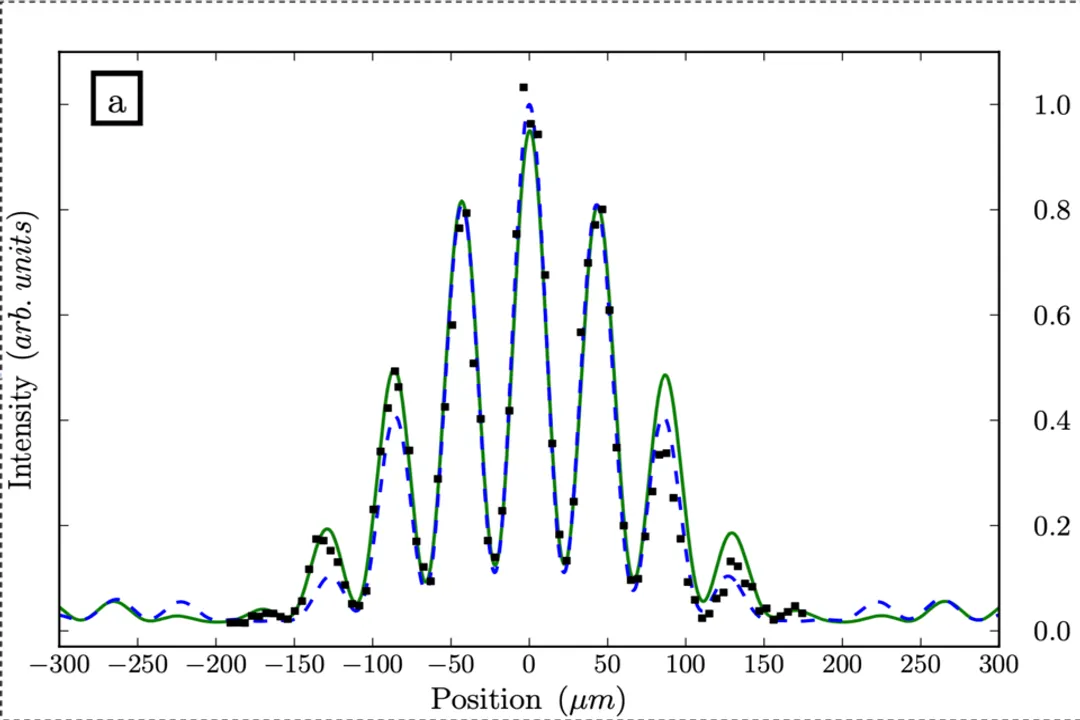
The most compelling evidence for the wave nature of matter comes from the famous double-slit experiment. When a stream of quantum entities, such as electrons or even small molecules, is fired at a barrier with two narrow slits, they do not simply pile up behind the slits as expected of classical particles. Instead, they create an interference pattern on a screen placed behind the barrier—a signature phenomenon exclusive to waves.
When the particles pass through the apparatus, they behave as if they traverse both slits simultaneously, interfering with themselves on the way to the screen, much like water waves would. This implies that the particle's description must involve a wave function () that spreads out in space and evolves according to the Schrödinger equation.
However, the duality becomes starkly apparent when we attempt to determine which slit the particle actually passed through. Introducing a detector to measure the path forces the quantum system to abandon its wave-like distribution and yield a definite, localized particle result at one slit or the other. The act of measurement appears to collapse the probability wave into a specific location, thereby destroying the interference pattern. This complementarity—the idea that wave behavior and particle behavior cannot be observed simultaneously in the same measurement—is a key descriptor of the phenomenon.
# Underlying Quantum Structure
To truly address what causes this duality, one must step away from classical analogies and look at the mathematical necessity within quantum mechanics. The standard mathematical description, governed by quantum field theory or wave mechanics, inherently includes both aspects because the physical observables (like position and momentum) do not commute. This non-commutativity is mathematically encoded by the relationship between operators representing these quantities, which is directly tied to Planck's constant.
Think of it this way: in classical physics, the path of an object is definite, described by precise coordinates in space and time. In quantum mechanics, the state of a system is described by a wave function, which dictates probabilities rather than certainties. The wave function evolves continuously and deterministically, exhibiting wave characteristics like superposition and interference. Yet, the measurement process extracts a single value, often localized, which is the particle aspect. The cause, therefore, is the fundamental formalism required to describe reality at scales where the quantization of action (represented by ) becomes significant.
An insightful way to view this causality: Imagine a universe where was arbitrarily large—say, the size of a baseball. Then, any object with the momentum of a baseball would have a macroscopically large, easily detectable wavelength. Conversely, if were infinitesimally small, the wave nature of an electron would be so subtle as to be practically undetectable, and physics would look classical. The duality arises because exists at a scale where it profoundly influences the dynamics of subatomic objects, forcing reality to obey a mathematics that encompasses both the continuous propagation (wave) and the discrete interaction (particle).
The wave is not something that turns into a particle; the quantum object is simply what it is, and when probed for position, it gives a particle answer, and when probed for momentum/path, it gives a wave answer. There is no known classical mechanism that bridges the gap, because the duality is a statement about the limits of classical description itself.
# Complementarity and Measurement
Niels Bohr introduced the principle of complementarity to formalize this observation. This principle asserts that wave and particle descriptions are mutually exclusive yet both necessary for a complete understanding of the quantum entity. One cannot observe both properties in the same experimental setup; the experiment dictates which aspect is revealed.
The apparent shift from wave to particle is often associated with the "collapse of the wave function" upon measurement, a concept that remains one of the most debated aspects of quantum interpretation. While this language describes what happens during observation, it does not fully explain the underlying cause of the duality itself, which pre-exists the measurement. The wave function exists and evolves as a wave, describing the potential for all possible outcomes, until an irreversible interaction—the measurement—occurs.
# Mathematical Necessity
The cause is fundamentally embedded in the mathematical structure itself. Consider the relationship between energy () and frequency () for a wave () and the energy of a particle ( for relativistic particles). The unified wave-particle description requires these relationships to be consistent across different energy and momentum states.
If we look at how physical properties are represented in quantum mechanics, they correspond to mathematical operators. For a particle, position () and momentum () are represented by operators that do not commute: , where . This fundamental non-commutativity mathematically forces the Heisenberg Uncertainty Principle, which states that position and momentum cannot both be known precisely simultaneously. A perfect particle has perfectly defined position but no wave-like distribution, while a perfect wave has perfectly defined momentum (wavelength) but is spread out, having no definite position. The duality is the inescapable result of this non-commuting structure required to describe reality at the quantum scale.
A helpful conceptual tool, though not a physical cause, is to imagine the quantum object not as a tiny ball or a ripple in water, but as a probabilistic cloud or "potentiality" governed by the wave equation. The particle aspect only appears when we force this potentiality to interact with a macroscopic measuring device. The "cause" is therefore the mathematical necessity of describing this potentiality with wave mathematics () while simultaneously acknowledging that our interaction with it is quantized and localized (particle detection).
# Duality Across Scales
It is essential to note that wave-particle duality applies to everything—you, me, and the computer screen—because every massive object has an associated de Broglie wavelength. The reason we never observe macroscopic objects exhibiting wavelike interference is simply the scale of Planck's constant relative to macroscopic momentum. For a baseball thrown at , the momentum is large, making the wavelength incredibly small—far too small to ever measure or detect any interference effects.
| Object | Momentum () (Approx.) | Planck's Constant () | de Broglie Wavelength () | Observable Feature |
|---|---|---|---|---|
| Electron | ( visible light) | Wave interference is easily seen | ||
| Baseball | Purely particle-like |
This table highlights that the cause is universal ( is constant), but the effect (observable duality) is scale-dependent. The mathematics of quantum mechanics is the cause; the measurement technique is the revealer.
# Interpretation Debates
While the experimental results confirming duality are certain, the underlying why often leads into philosophical territory regarding quantum mechanics interpretation. Some interpret duality as evidence that the quantum world is fundamentally probabilistic, where reality only solidifies upon measurement, which itself is an irreversible process. Others maintain a more deterministic view where the wave function never truly collapses, but our knowledge of the system becomes constrained by the measurement apparatus. Regardless of the philosophical stance on collapse, the mathematical need for both wave and particle descriptions remains the constant feature imposed by experiments like the double-slit test. The mechanism that causes the switch, if one insists on seeing a switch, is tied directly to how information is extracted from the quantum system, forcing the quantum description () to project onto the classical measurement basis.
The core takeaway is that wave-particle duality is not an anomaly caused by external forces or hidden variables acting on an object; it is an intrinsic property arising from the fact that energy and action are quantized by Planck's constant, necessitating a mathematical structure where localized energy (particle) and extended probability (wave) are two inseparable facets of the same underlying reality.
#Videos
Wave Particle Duality Explained | Perimeter Institute for Theoretical ...
Related Questions
#Citations
Wave–particle duality - Wikipedia
Wave Particle Duality Explained | Perimeter Institute for Theoretical ...
What causes wave-particle duality? - Quantum Physics. - Quora
Wave/particle duality : r/PhilosophyofScience - Reddit
What is the mechanism behind the wave - particle duality
Understanding Wave-Particle Duality in Quantum Mechanics
Wave-Particle Duality
Wave-Particle Duality - Chemistry LibreTexts
The surprising origins of wave-particle duality - Big Think
The Quantum Leap's Beginner Guide to “Wave-Particle Duality”