What formula formalizes Louis de Broglie's hypothesis connecting a particle's momentum ($p$) to its associated wavelength ($\lambda$)?
Answer
\lambda = h/p
The de Broglie relation, \lambda = h/p, connects the particle's momentum ($p$) to its wave characteristic (wavelength $\lambda$) using Planck's constant ($h$).
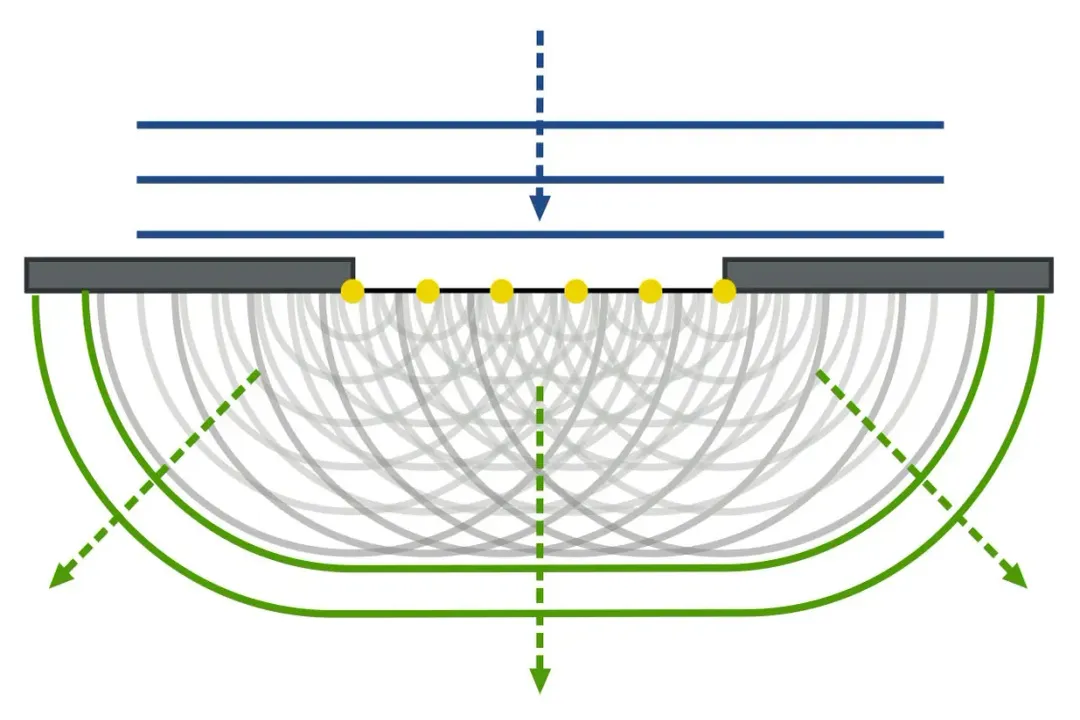
#Videos
Wave Particle Duality Explained | Perimeter Institute for Theoretical ...
Related Questions
What inherent quality do objects like photons possess according to modern understanding?Which historical phenomenon demonstrated that light energy transfer occurs in discrete packets called quanta?What formula formalizes Louis de Broglie's hypothesis connecting a particle's momentum ($p$) to its associated wavelength ($\lambda$)?If Planck's constant ($h$) were zero, what would be the consequence for physical behavior?What signature phenomenon on a screen confirms the wave nature of matter in the double-slit experiment?What concept did Niels Bohr introduce to describe that wave and particle descriptions are mutually exclusive yet both necessary for completeness?What is the fundamental mathematical requirement cited as the underlying cause of wave-particle duality?What happens to the wave-like distribution when a measurement attempts to determine which slit a particle passed through?What relationship mathematically defines the non-commutativity between the position ($\hat{x}$) and momentum ($\hat{p}$) operators?Why do macroscopic objects, such as a baseball, not exhibit observable wave interference effects?