What model did Kepler use?
Johannes Kepler inherited a universe in transition, a celestial stage where the long-reigning Ptolemaic system was being vigorously challenged by the newly championed Copernican view. To understand the model Kepler ultimately adopted, one must first appreciate the models he sought to perfect or overthrow. The question wasn't just what shape the heavens took, but who stood at the center of motion. The entire astronomical community was grappling with the mathematical and philosophical implications of these competing worldviews, setting the stage for Kepler’s own radical revisions.
# Ancient Foundation

For over a millennium, the standard understanding of the cosmos was the model devised by Claudius Ptolemy, which placed the Earth firmly at the center—a geocentric system. This model was appealing because it matched everyday observation: the Sun, Moon, and stars certainly appeared to revolve around us daily. To account for the perplexing retrograde motion of the planets—where they occasionally seemed to pause, move backward briefly, and then resume their forward path—Ptolemy employed complex mechanisms known as epicycles (small circles upon larger circles) and deferents. While mathematically cumbersome, the Ptolemaic system was remarkably accurate for its time, making predictions with enough precision to satisfy practical needs, like calendar-making.
# Copernican Theory
The first major conceptual shift came centuries later with Nicolaus Copernicus, who proposed a heliocentric system where the Sun was placed at the center of the known planets, including Earth, which was now just another planet orbiting it. The primary appeal of the Copernican model was its inherent mathematical elegance; it explained retrograde motion naturally as an optical illusion caused by Earth overtaking slower-moving outer planets or being overtaken by faster-moving inner ones. However, Copernicus did not entirely dispense with the ancient Greek preference for perfect heavenly motion. To keep his model aligned with existing observations (which were still based on older, less precise measurements), Copernicus largely retained the use of circular orbits and epicycles, albeit fewer than Ptolemy required. This meant that while conceptually superior, Copernicus’s actual predictive power wasn't dramatically better than the Ptolemaic system, which left many astronomers unconvinced, particularly given the theological implications of shifting Earth from its central, privileged position.
# Tychonic Compromise

Before Kepler fully committed to a purely Sun-centered universe based on true ellipses, a third major model gained significant traction: the system proposed by Tycho Brahe. Tycho, a brilliant observational astronomer, constructed a hybrid system that attempted to reconcile the observational benefits of Copernicanism with the philosophical acceptance of a stationary Earth. In the Tychonic model, the Earth remained the static center of the universe. The Moon and the Sun revolved around the Earth, but all the other known planets—Mercury, Venus, Mars, Jupiter, and Saturn—were described as orbiting the Sun. This geo-heliocentric structure was an intellectual compromise designed to preserve Earth's centrality while mathematically accounting for the observed planetary positions.
# Data Foundation
The essential bridge between these historical models and Kepler’s final theory was not philosophy but data. Tycho Brahe spent decades meticulously tracking planetary positions with unprecedented accuracy, gathering the most precise raw observational data available up to that point. Kepler, initially an advocate for the Copernican model, became Tycho's assistant in Prague. After Tycho’s death, Kepler inherited this massive, high-quality dataset, particularly the extensive records for the orbit of Mars. Kepler spent years attempting to fit Tycho's observations, especially those for Mars, into the sacred circular orbits required by both Ptolemy and Copernicus.
The discrepancy was frustratingly small but persistent. No matter how many epicycles or equants Kepler tried, the calculated positions based on a circular orbit for Mars deviated from Tycho’s observations by about eight arcminutes. In the grand scale of the heavens, eight arcminutes seems negligible, but for Tycho’s data, it was an irreconcilable error. This is where Kepler’s genius and persistence truly shone. He famously described this moment as a necessary recognition that a deviation of eight minutes of arc is not a mistake in the measurement, but a mistake in the assumption.
# Elliptical Paths
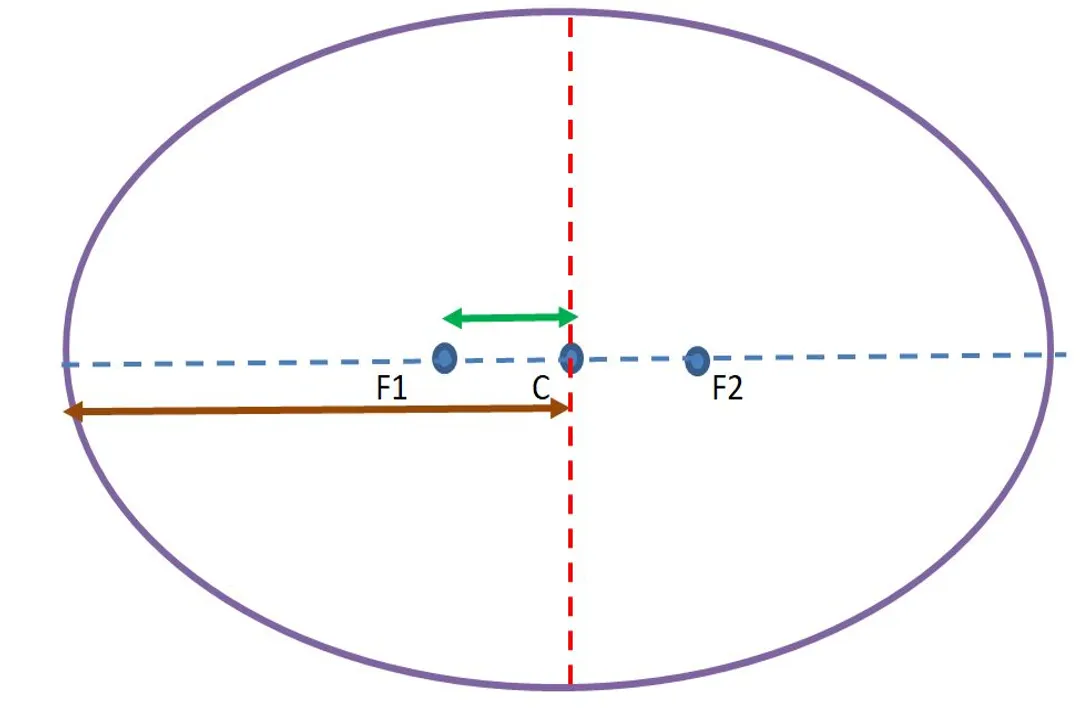
Kepler's model, developed in his work Astronomia Nova (1609), discarded the circular dogma that had constrained astronomy since antiquity. He concluded that the true path of the planets was not a circle, but an ellipse, with the Sun situated at one of the two foci of that ellipse. This marked the foundation of Kepler's first and second laws of planetary motion.
Kepler's resulting model is defined by three fundamental laws:
- Law of Orbits: Planets move in ellipses with the Sun at one focus.
- Law of Areas: A line joining a planet and the Sun sweeps out equal areas during equal intervals of time. This inherently explains why planets move faster when closer to the Sun and slower when farther away, resolving the non-uniform speed issue without complex epicycles.
- Law of Periods: The square of a planet's orbital period () is proportional to the cube of the semi-major axis () of its orbit ().
The model Kepler utilized was therefore a mathematically precise, physically motivated heliocentric system—a Keplerian model—that used elliptical geometry rather than epicycles to describe planetary motion perfectly. This was a radical departure from the geometric assumptions of the past.
| Model | Center of Orbit | Path Shape Assumed | Complexity Mechanism |
|---|---|---|---|
| Ptolemaic | Earth | Circles | Epicycles and Deferents |
| Copernican | Sun | Circles (with some modification) | Minor Epicycles |
| Tychonic | Earth (Planets orbit Sun) | Circles | Required no planetary epicycles |
| Keplerian | Sun (at one focus) | Ellipses | None required |
It is important to recognize that Kepler's model was deeply rooted in the Copernican concept (Sun-centered) but was mathematically distinct due to the elliptical reality. His goal, in many ways, was to provide the Copernican system with the mathematical rigor it previously lacked, which he achieved by fully embracing non-circular geometry.
# Mathematical Purity Shattered
The shift from circles to ellipses represents more than just a geometric tweak; it signifies a profound epistemological break in astronomy. For thousands of years, the circle represented perfection, divinity, and the immutable order of the heavens. Philosophers and astronomers alike believed celestial motions must conform to this ideal shape, making any deviation a sign of flawed observation or incomplete theory. Kepler’s struggle with Mars was the struggle against this inherited aesthetic bias. He had to force himself to look at the data without the a priori assumption that the orbits had to be perfect circles. This move from valuing philosophical aesthetics to prioritizing empirical data, even when it contradicted long-held ideals, is a crucial aspect of Kepler's adopted model. It’s a case study in scientific maturation, where admitting an 'ugly' but accurate solution (the ellipse) proves superior to clinging to a 'beautiful' but flawed one (the circle).
# Beyond Description
Kepler’s model, while fundamentally a descriptive geometric account of how the planets moved, hinted at a deeper underlying why that set the stage for Newton. While the Ptolemaic and Copernican systems described paths using pure geometry, Kepler began to infuse his laws with a physical reality based on a concept of motive force originating from the Sun. He theorized that the Sun exerted a kind of magnetic or physical influence that caused the planets to move. The Law of Areas is especially telling here. If motion is caused by a force radiating from the Sun, a planet traveling farther away would naturally slow down as the influence weakens over distance, which is precisely what the area law describes. Although Kepler did not articulate the modern concept of universal gravitation, his model implicitly required a physical mechanism tied to the central body, something entirely absent from purely geometric models like Ptolemy's or even the early Copernican efforts. This step—from describing what happens to suggesting what causes it to happen—is perhaps the most valuable, enduring legacy of the model Kepler finally settled upon. This laid essential groundwork for Isaac Newton’s later development of the universal law of gravitation.
In summary, the model Johannes Kepler used was the culmination of centuries of astronomical thought. He started by trying to refine the Copernican heliocentric structure using the Tychonic data, ultimately concluding that neither perfect circles nor epicycles were necessary. His final, established model was the Keplerian Heliocentric System defined by elliptical orbits and his three mathematical laws, a system that finally achieved accuracy because it mirrored the physical reality observed by Tycho Brahe.
Related Questions
#Citations
Heliocentrism - Wikipedia
Three Models - Kepler's Discovery
Orbits and Kepler's Laws - NASA Science
Copernicus, Galileo, Kepler - history of astronomy : r/askastronomy
Whose Revolution? Copernicus, Brahe & Kepler - Library of Congress
Johannes Kepler: Everything you need to know - Space
Picturing the solar system: a tale of astronomical change
Heliocentric model - The Solar System Wiki - Fandom
Kepler's Model of the Solar System
Johannes Kepler - Explaining Science