Which of the following laws do astronomers use to determine the mass of stars using observations of binary star systems?

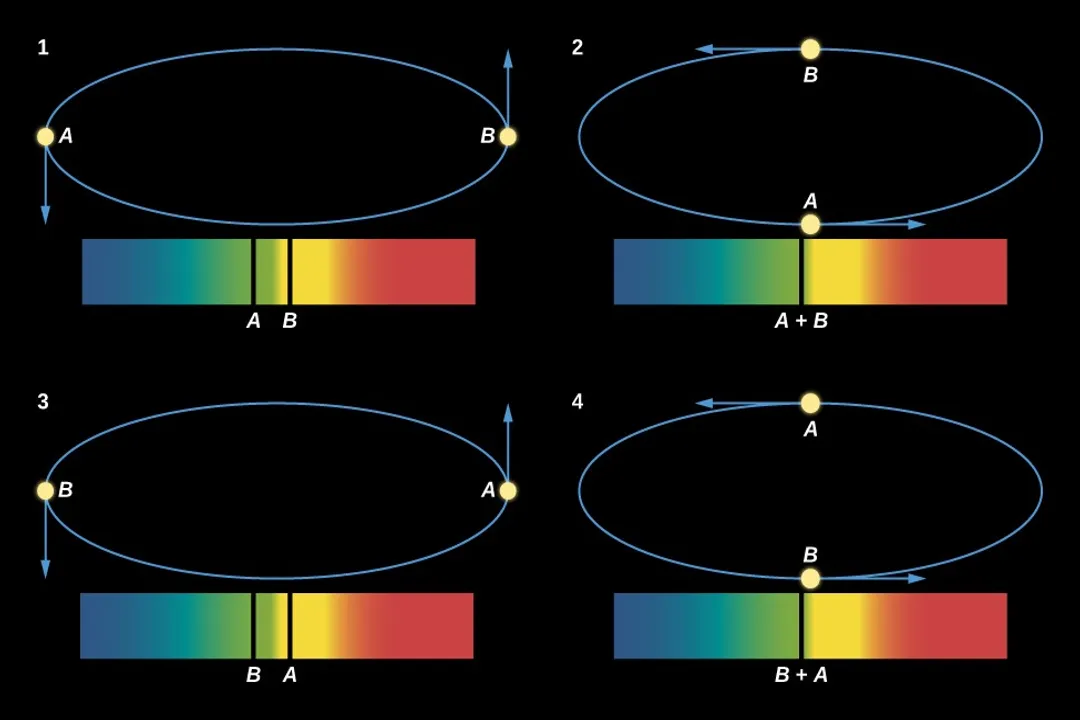
The most direct method astronomers have for weighing stars, those distant suns that appear as simple points of light, involves looking closely at systems where two stars orbit a common center of mass. These are known as binary star systems. By observing the orbital motions of these companions, particularly their period and separation, astronomers can apply fundamental laws of physics to deduce their masses. The key physical principle underpinning this determination is a crucial extension of Kepler's Third Law of Planetary Motion.

# Kepler's Law

The law connecting orbital period and separation is Kepler's Third Law. This law, originally formulated based on observations of our solar system, relates the square of the orbital period ($P$) of a planet to the cube of the semi-major axis ($a$) of its orbit. However, when dealing with two stars orbiting each other, astronomers must employ a more general form of this law that incorporates gravity, derived from Newton's Law of Universal Gravitation.

The general form of the law used for binary systems relates the sum of the masses ($M_1 + M_2$) to the orbital period ($P$) and the semi-major axis ($a$) of the relative orbit. The precise equation, sometimes referred to as the Newtonian form of Kepler's Third Law, is often written as:

$$(M_1 + M_2) = \frac{a^3}{P^2}$$

When using standard astronomical units—where $P$ is measured in years, $a$ in astronomical units (AU), and the total mass $(M_1 + M_2)$ is expressed in solar masses ($M_\odot$)—the constant of proportionality ($G$, the gravitational constant) conveniently cancels out, simplifying the relationship immensely. In this specific context, the full expression is:

$$(M_1 + M_2) = \frac{a^3}{P^2}$$

This equation yields the sum of the masses of the two stars, $M_1$ and $M_2$, provided the orbital period $P$ and the semi-major axis $a$ are known. Determining the individual masses requires an additional piece of information.

This application of celestial mechanics demonstrates that the laws used are fundamentally rooted in Newtonian mechanics as applied to two-body orbits, which refines Kepler's original empirical observations. Astronomers must be able to accurately measure these orbital characteristics from observations of the system.

# Mass Ratios

Simply knowing the total mass, $M_1 + M_2$, is often insufficient for a complete stellar analysis. To separate the individual masses, one must account for the center of mass. The center of mass of the system dictates that the distance each star is from this center is inversely proportional to its mass. If $a_1$ is the semi-major axis of star 1's orbit around the center of mass and $a_2$ is the semi-major axis of star 2's orbit, then the relationship is:

$$M_1 a_1 = M_2 a_2$$

This leads to the mass ratio:

$$\frac{M_1}{M_2} = \frac{a_2}{a_1}$$

Combining this ratio with the total mass equation allows for the calculation of $M_1$ and $M_2$ individually. However, extracting $a_1$ and $a_2$ directly can be challenging. Often, astronomers measure the angular separation $\alpha$ and the distance to the system $d$. The true separation $a$ is $a_1 + a_2$, which in angular terms, requires knowing the true distance $d$.

What did Galileo use to study the stars?

# Inclination Dependency

A significant difficulty in applying these laws arises from the geometry of the observation. The calculated orbital period $P$ is usually the true period, as orbital motion is essentially a closed loop. The challenge lies in the semi-major axis $a$. When observing a binary system, we only see the projection of the orbit onto the plane of the sky.

If the orbital plane is perfectly face-on to Earth, we measure the true semi-major axis $a$ directly. However, if the orbit is tilted by an angle $i$ relative to our line of sight—the inclination—the measured separation is foreshortened. The measured semi-major axis, denoted as $a \sin(i)$, is less than the true value $a$ unless $i = 90^\circ$.

Because the mass equation depends on $a^3$, the unknown inclination $i$ introduces a strong dependency on the calculated masses. If we mistakenly use the observed projected separation ($\alpha$) instead of the true semi-major axis ($a$), we calculate a minimum mass, often denoted as $M \sin^3(i)$.

This introduces the concept of the Binary Mass Function. The mass function is an expression derived from Kepler's law that depends only on the observable quantities of the orbital period ($P$), the semi-major axis projection ($a \sin i$), and the inclination, but it does not require knowing the true $a$ or $i$ individually to provide a lower limit on the total mass.

The simplified mass function, when $M_1 \ll M_2$ (i.e., one star is much less massive than the other, which is often the case for a compact object orbiting a main-sequence star), is given by:

$$f(M) = \frac{(M_2 \sin i)^3}{(M_1 + M_2)^2} \approx M_1 \sin^3 i$$

While this function itself depends on $i$, it allows astronomers to set a firm lower bound on the mass of the unseen component, $M_1$. If an astronomer calculates a minimum mass, say $M_{min}$, the true mass $M$ must be greater than or equal to $M_{min}$.

Consider a compact object like a neutron star or a black hole, often found in X-ray binaries such as Cygnus X-1. If observations show a minimum mass for the companion star that exceeds $3 M_\odot$, it strongly suggests the unseen object is not a neutron star (whose maximum mass is thought to be around $2$ to $3 M_\odot$), but rather a black hole, as its mass must be greater than the calculated lower limit. The derived minimum mass is a critical tool precisely because the inclination is unknown.

# Observational Classification

The way astronomers measure $P$ and $a$ depends on the type of binary system observed. There are three primary classifications relevant to mass determination:

1. Visual Binaries: Both stars can be seen separately through a telescope. Astronomers can track the orbits over many years, directly measuring the angular separation and period, allowing for a more direct calculation of $a$ if the distance $d$ is known.
2. Spectroscopic Binaries: The stars are too close to be visually resolved, but their orbital motion causes shifts in their spectral lines due to the Doppler effect. As a star moves toward us, its lines are blue-shifted; as it moves away, they are red-shifted. This allows for the measurement of the orbital velocity, from which $P$ can be derived, and often provides clues about the inclination and mass ratio.
3. Eclipsing Binaries: The orbital plane is viewed nearly edge-on ($i \approx 90^\circ$). When one star passes in front of the other, the total light from the system dims, producing a light curve. For these systems, the measured separation is very close to the true semi-major axis ($a \sin i \approx a$), making the mass calculation much more direct and accurate, as the inclination uncertainty is minimized.

A system that is both spectroscopic and eclipsing (a spectroscopic eclipsing binary) provides the best possible scenario for mass determination because both velocity curves (from Doppler shifts) and the inclination (from eclipses) are known.

How does mass impact a star?

# Applying Conservation Laws

The underlying physics that validates the use of Kepler's Third Law in its Newtonian form stems from the conservation of momentum and conservation of energy. The center of mass of the two-star system remains stationary in the absence of external forces, which leads directly to the relationship $M_1 a_1 = M_2 a_2$. Furthermore, the total energy of the system, which involves both kinetic and gravitational potential energy, is conserved throughout the orbit.

When we look at the formula derived from the conservation laws, we see that the period $P$ is related to the gravitational parameter $\mu = G(M_1+M_2)$ and the semi-major axis $a$. The formula itself, $(M_1 + M_2) = a^3 / P^2$ (in solar units), is elegant because it shows that for a given orbital size and period, the total mass contained within that orbit is fixed, regardless of the individual masses or the eccentricity of the orbit.

Here is a point to consider when practicing these calculations: Imagine two stars orbiting with a 10-year period ($P=10$ yr). If they are observed to have a large separation of $a=10$ AU, the total mass is $(10^3) / (10^2) = 100/100 = 1$ solar mass ($M_\odot$). If you instead observe an eclipsing binary with the exact same period ($P=10$ yr) but they appear much closer, say $a=1$ AU, the total mass must be dramatically lower: $(1^3) / (10^2) = 1/100 = 0.01 M_\odot$. This demonstrates the extreme sensitivity of the total mass calculation to the cubed separation and the inverse squared period.

For general physics students applying this, it is crucial to remember that the 'a' in the equation is the semi-major axis of the relative orbit, which is the distance between the two stars' centers in the absence of eccentricity, and it must be calculated from the measured angular separation ($\alpha$) multiplied by the distance to the system ($d$): $a = \alpha \cdot d$. If the system is not eclipsing, $\alpha$ is an underestimate of the true $a$, leading to the inclination issue discussed previously.

# Unseen Companions

The ability to determine mass using this method is not limited to systems where both stars are visible. This is particularly important when one star has evolved into a compact remnant, such as a white dwarf, neutron star, or black hole.

In systems where one star is invisible (perhaps because it is too faint or completely obscured), the light curve and spectral shifts are dominated by the visible star. We can still measure its velocity ($v_1$) and orbital period ($P$). From this, we can calculate the projected semi-major axis of the visible star's orbit ($a_1 \sin i$) using the relationship $a_1 \sin i = v_1 P / (2\pi)$ (when $v_1$ is correctly calculated from Doppler shifts).

By substituting this projected term into the mass function, astronomers can constrain the mass of the unseen companion ($M_2$). If the visible companion ($M_1$) is very small, the mass function approximates the mass of the unseen companion multiplied by $\sin^3 i$. This is the power of the Binary Mass Function: it provides a firm, measurable lower limit on the mass of the missing object, which is often sufficient to classify the nature of that invisible object. For instance, in a binary system, if the invisible companion's mass function calculation yields a