What determines molecular geometry?

The three-dimensional arrangement of atoms in a molecule, known as its molecular geometry, dictates many of its chemical and physical properties, such as polarity, reactivity, and how it interacts with other molecules. ^[2][3] Understanding this shape is fundamental to comprehending chemical behavior, and fortunately, predicting it relies on a remarkably consistent model that focuses almost entirely on the electron pairs surrounding the central atom. ^[1][5]

# Electron Domains

The entire concept of predicting molecular shape hinges on the idea that electron pairs in the valence shell of the central atom repel one another. ^[1][4][8] This repulsion forces the electrons, and thus the attached atoms, into positions that maximize the distance between them. ^[1][4] These regions of electron density are referred to as electron domains. ^[1][9]

An electron domain can be either a bonding pair (a single, double, or triple bond) or a lone pair of electrons that is not shared with another atom. ^[1][5][9] It is important to remember that, for the purposes of determining the initial geometry, a multiple bond (like a double or triple bond) counts as only one electron domain. ^[1][5][7] For instance, the carbon dioxide molecule (${\text{CO}}_2\backslash text\{CO\}\_2$) has two double bonds, resulting in two electron domains around the central carbon atom. ^[1]

The process for determining geometry generally begins with drawing the Lewis structure to identify the central atom and count the total number of electron domains surrounding it. ^[1][5][8] This total count—the sum of bonding domains and lone pairs—determines the electron geometry. ^[1][7][9] The electron geometry describes the arrangement of all electron domains, including the lone pairs, in space. ^[1]

# Repulsion Forces

While all electron domains repel each other, the strength of this repulsion is not uniform. ^[1][6] The fundamental rule of thumb, central to the Valence Shell Electron Pair Repulsion (VSEPR) theory, establishes a hierarchy of repulsion strength. ^[1][4][9]

The greatest repulsion occurs between two lone pairs. ^[1][6] A lone pair occupies more space around the nucleus than a bonding pair because it is held by only one nucleus, allowing it to spread out more freely. ^[1][4] Therefore, lone pairs will try to position themselves as far apart as possible from other lone pairs. ^[1] Following lone pairs in terms of repulsive power are multiple bonds (double or triple bonds) compared to single bonds. ^[1]

The hierarchy of repulsion is typically ordered as follows:

• Lone Pair - Lone Pair > Lone Pair - Bonding Pair > Bonding Pair - Bonding Pair ^[1][4]

This difference in repulsion is critical because while the electron geometry is dictated by the total number of domains, the observed molecular geometry—the shape formed by the atoms—is determined after accounting for the positioning of the lone pairs. ^[1][7] Lone pairs essentially push the surrounding bonding pairs closer together, distorting the idealized shape predicted by simple geometry. ^[1][6]

What determines color perception?

# Geometry Shapes

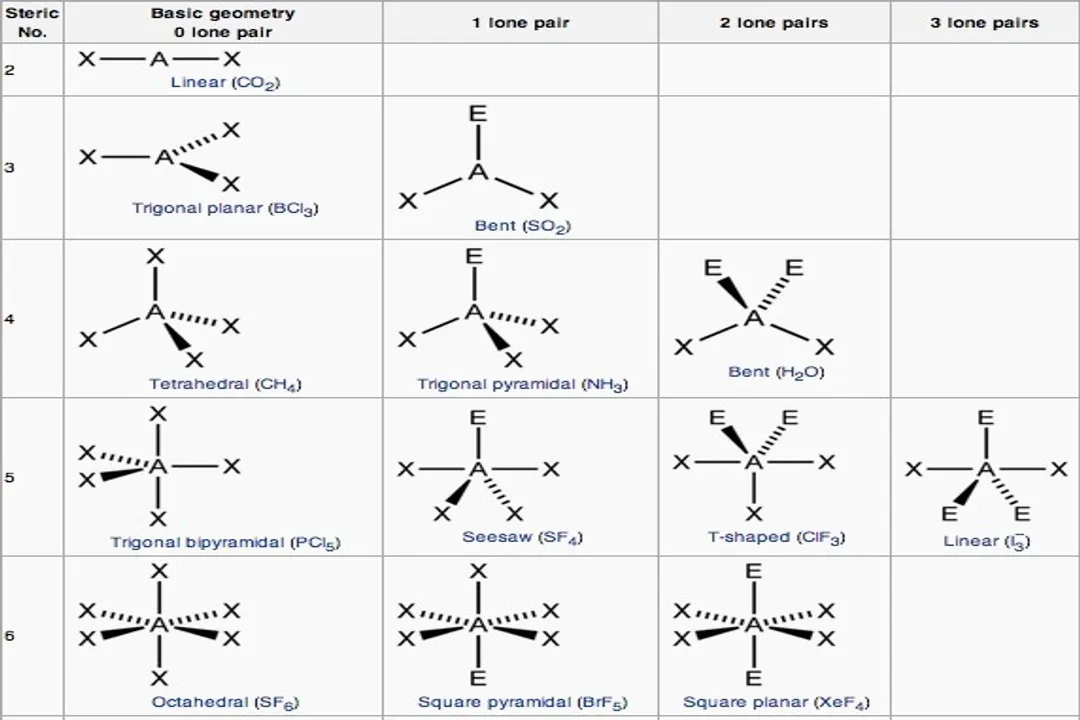
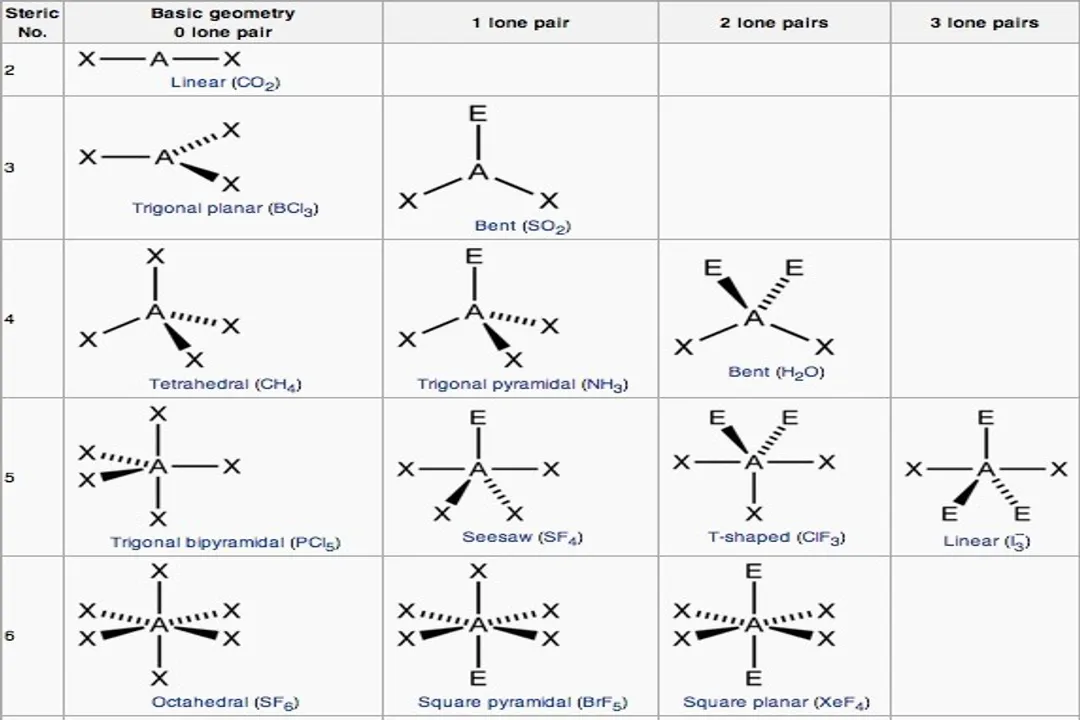
The VSEPR model predicts specific electron geometries based on the number of electron domains (2 through 6 are most common). ^[1][8] For example, two domains lead to a linear electron geometry, three domains to trigonal planar, and four domains to tetrahedral. ^[1][7]

However, the final molecular geometry depends on how many of those domains are lone pairs. Consider the case of four total electron domains (a tetrahedral electron geometry, with an ideal ${109.5}^{\circ }109.5^\backslash circ$ bond angle): ^[1][8]

• Four Bonding Pairs, Zero Lone Pairs (${\text{AX}}_4\backslash text\{AX\}\_4$): The molecular geometry is Tetrahedral (e.g., ${\text{CH}}_4\backslash text\{CH\}\_4$). ^[1][7]
• Three Bonding Pairs, One Lone Pair (${\text{AX}}_3\text{E}\backslash text\{AX\}\_3\backslash text\{E\}$): The lone pair compresses the bond angles. The resulting molecular geometry is Trigonal Pyramidal (e.g., ${\text{NH}}_3\backslash text\{NH\}\_3$). ^[1][7]
• Two Bonding Pairs, Two Lone Pairs (${\text{AX}}_2{\text{E}}_2\backslash text\{AX\}\_2\backslash text\{E\}\_2$): The two lone pairs exert strong repulsion, leading to a Bent or V-shaped molecular geometry (e.g., ${\text{H}}_2\text{O}\backslash text\{H\}\_2\backslash text\{O\}$). ^[1][7]

When we move to five and six electron domains, the structural possibilities become even more varied due to the required positions for lone pairs, which often occupy equatorial positions to minimize 90-degree interactions. ^[1][4]

For five domains (Trigonal Bipyramidal electron geometry), a single lone pair results in a Seesaw shape, and two lone pairs result in a T-shaped geometry. ^[1][7] When there are six domains (Octahedral electron geometry), one lone pair yields a Square Pyramidal shape, and two lone pairs result in a Square Planar shape. ^[1][7]

Here is a summary of the most common electron domain counts and their resulting geometries, noting the influence of lone pairs:

# Angle Variations

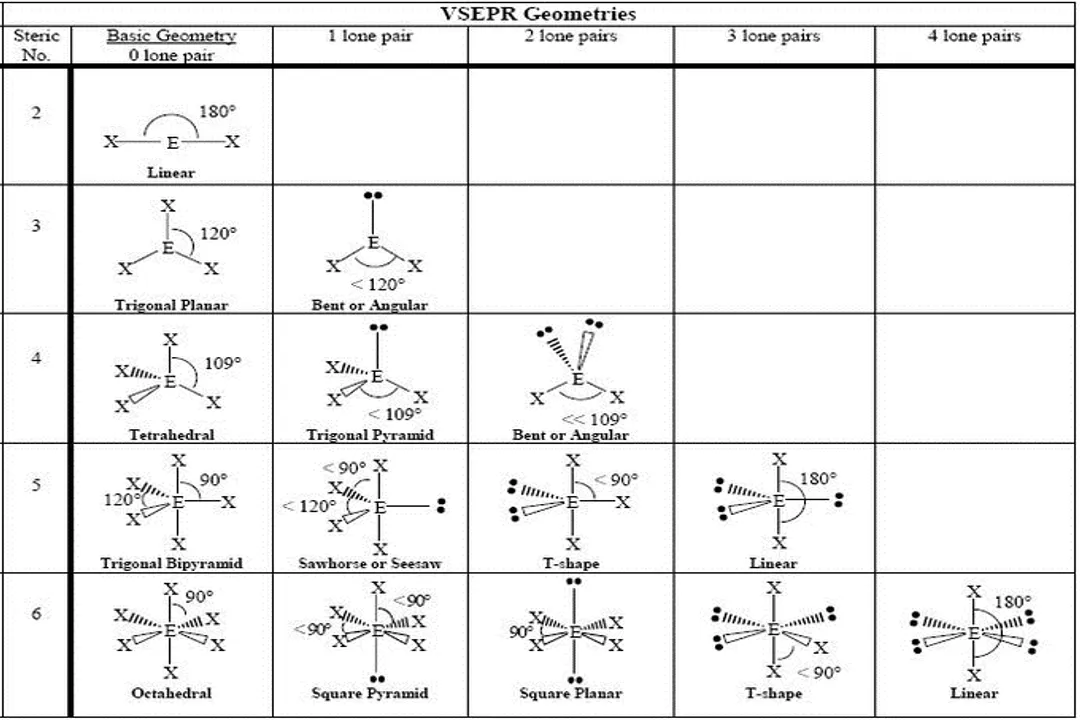
The idealized bond angles associated with perfect VSEPR geometries—like the ${109.5}^{\circ }109.5^\backslash circ$ in a perfect tetrahedron or ${120}^{\circ }120^\backslash circ$ in a trigonal planar system—are often slightly altered in real molecules. ^[4] This deviation occurs primarily because of the differing repulsion strengths between electron domains. ^[1][4]

For instance, in ammonia (${\text{NH}}_3\backslash text\{NH\}\_3$), the electron geometry is tetrahedral, suggesting a ${109.5}^{\circ }109.5^\backslash circ$ angle. ^[1] However, the lone pair on the nitrogen atom exerts a stronger repulsion than the three N-H bonding pairs. This stronger repulsion pushes the three hydrogen atoms closer together, compressing the actual bond angle to about ${107}^{\circ }107^\backslash circ$. ^[1][6] Water (${\text{H}}_2\text{O}\backslash text\{H\}\_2\backslash text\{O\}$) has two lone pairs, leading to even greater repulsion and a smaller bond angle, approximately ${104.5}^{\circ }104.5^\backslash circ$. ^[1]

When comparing different molecules with the same general VSEPR type, like comparing methane (${\text{CH}}_4\backslash text\{CH\}\_4$) to chloromethane (${\text{CH}}_3\text{Cl}\backslash text\{CH\}\_3\backslash text\{Cl\}$), the central atom's identity and the surrounding atoms’ electronegativity can subtly adjust these angles. While the VSEPR model simplifies this by focusing on the number of domains, a deeper look reveals that the nature of the bonding atoms matters. For example, the $\text{Cl}-\text{C}-\text{H}\backslash text\{Cl\}-\backslash text\{C\}-\backslash text\{H\}$ bond angle in chloromethane will differ slightly from the $\text{H}-\text{C}-\text{H}\backslash text\{H\}-\backslash text\{C\}-\backslash text\{H\}$ angle because chlorine is more electronegative than hydrogen, pulling electron density away from the carbon center and slightly altering the effective size and repulsion exerted by the C-Cl bond compared to the C-H bonds. ^[4]

A useful way to think about this compression effect is to assign 'space requirements.' A lone pair demands the most physical space in the valence shell, followed by double bonds, then single bonds. Any time you place two high-demand residents (like two lone pairs) next to each other in a trigonal bipyramidal arrangement, the resulting geometric squeeze on the axial neighbors is significant, forcing those bond angles down toward ${90}^{\circ }90^\backslash circ$ from the ideal ${120}^{\circ }120^\backslash circ$. ^[1]

What determines pitch and loudness?

# Application Checklist

To reliably predict the geometry of any simple covalent molecule, one can follow a systematic checklist based on these principles. ^[5][8] This stepwise approach ensures that the nuances of lone pair placement are addressed correctly:

1. Draw the Lewis Structure: Determine the total number of valence electrons for the molecule. ^[8]
2. Count Electron Domains: Identify the central atom and count the total number of regions of electron density around it (single, double, or triple bonds count as one region each; count all lone pairs separately). ^[1][5]
3. Determine Electron Geometry: Based on the total domain count, assign the ideal electron geometry (e.g., 4 domains = Tetrahedral). ^[1]
4. Identify Lone Pairs: Note how many of the domains are lone pairs. ^[9]
5. Determine Molecular Geometry: Use the domain count and the lone pair count to establish the specific molecular geometry (e.g., 4 domains total, 1 lone pair = Trigonal Pyramidal). ^[5][7]
6. Predict Angles: Use the electron geometry's ideal angle as a starting point, then reduce it based on the number and position of lone pairs, applying the knowledge that lone pairs cause compression. ^[1][4]

By consistently applying the VSEPR model—counting all electron domains and then factoring in the spatial dominance of lone pairs—we move from the abstract drawing on paper to the precise, three-dimensional shape that governs chemical reality. ^[2][3]