What is the law of large numbers?
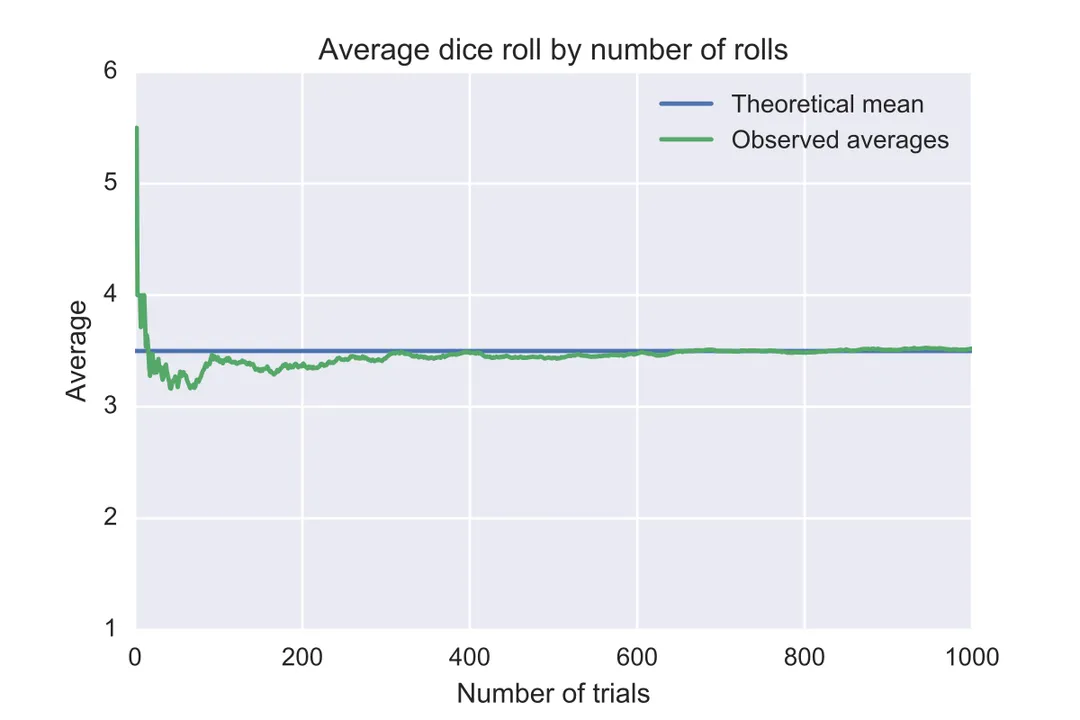
The convergence of randomness toward predictability is not just a philosophical concept; it is a cornerstone of modern statistics and decision-making, encapsulated in what is formally known as the Law of Large Numbers. At its most fundamental, this mathematical law dictates that if you repeat a random experiment an extensive number of times, the average of the actual outcomes you observe will drift closer and closer to the theoretical expected value. This principle is what gives confidence to everything from polling in elections to setting the baseline profitability for the world's largest casinos. It serves as the vital bridge connecting the abstract probabilities we calculate on paper to the messy, real-world results we see in practice.
If we consider a simple event, like flipping a fair coin, the expected value for heads is exactly 50%, or $0.5$. If you flip it ten times, observing seven heads (a $70%$ rate), the result is far from the theoretical average. However, if you continue flipping that same coin, now running the tally to ten thousand flips, the observed proportion of heads will be strikingly close to that $50%$ mark. The law guarantees that as the sample size—the number of trials or observations—increases, the sample mean becomes a more reliable, representative measure of the overall population mean.
# Core Mathematics
The formal definition rests on the concept of independent and identically distributed (i.i.d.) random variables. Let be a sequence of these variables, each having the same finite expected value, . The law concerns the sample average, denoted :
The law asserts that this sample average, , converges toward as (the sample size) approaches infinity.
This convergence can be understood through the lens of variance. When the variables are independent and share a finite variance, , the variance of the sample average itself shrinks proportionally to :
As grows, the variance of the average becomes tiny, meaning the sample mean is less likely to stray far from the true mean .
# Forms of Convergence
Mathematicians recognize this principle in two primary forms, distinguished by the mode of convergence they guarantee: the Weak Law and the Strong Law.
# Weak Law
The Weak Law of Large Numbers (WLLN), sometimes called Khinchin's law, states that the sample mean converges in probability to the expected value as the number of trials increases. In practical terms, for any tiny margin, , no matter how small you define it, the probability that the sample average will fall outside that margin approaches zero as goes to infinity. It means there is a high likelihood that the average will be "close enough" to the true mean when the sample is large.
# Strong Law
The Strong Law of Large Numbers (SLLN), or Kolmogorov's law, offers a more definitive statement, asserting convergence almost surely. This is a mathematically stricter condition. It means that the probability that the sequence of sample averages will eventually settle down and stay within any arbitrarily small distance of is equal to one. If the weak law says the average is likely to be close, the strong law says it will be close, with probability one, for all sufficiently large . Because almost sure convergence implies convergence in probability, the strong form is indeed more powerful in the mathematical sense.
# Dispelling Fallacies
The power of the Law of Large Numbers is often confused with a different, incorrect concept called the Gambler's Fallacy. This fallacy suggests that if a random event has an unusual streak—say, a die has landed on a '6' four times in a row—the next outcome is somehow due to be a non-'6' to correct the imbalance.
The Law of Large Numbers does not assert this correction mechanism for short-term results. Each new trial in a truly random process is independent; the coin or die has no memory. When discussing a fair coin, the probability of the next flip being heads remains , regardless of the previous twenty flips being tails.
It is a subtle but critical distinction: while the proportion of heads approaches over millions of flips, the absolute difference between the number of heads and the number of tails is expected to grow as the total number of flips grows. For example, after 100 flips, you might have 53 heads and 47 tails (a difference of 6). After 10,000 flips, you might have 5,030 heads and 4,970 tails (a difference of 60). The ratio ($50.3%$ vs. $50.03%$) gets closer to $0.5$, but the raw count difference increases. The law smooths out the relative frequency, not the absolute deviation from the mean. This smoothing process happens because the early outliers are overwhelmed by the sheer volume of later, more predictable outcomes, not because the universe balances the books immediately.
# Application in Risk and Estimation
The true utility of the LLN lies in transforming uncertainty into manageable risk by looking at aggregates. This is most evident in two major industries: insurance and gambling establishments.
In an insurance company setting, an underwriter cannot predict with certainty whether a single policyholder will make a major claim next year. If they only had ten clients, the risk is incredibly high, as one severe event could bankrupt the operation—this is the "law of small numbers" at play, where small samples are highly unrepresentative. By enrolling thousands or millions of policyholders, the company pools that extreme individual risk. The law of large numbers dictates that the actual claims paid out will hover very close to the statistical average cost calculated based on historical data for that demographic.
Consider the following hypothetical comparison for a simple car insurance pool:
| Metric | Small Sample (100 Drivers) | Large Sample (100,000 Drivers) |
|---|---|---|
| Expected Claims Cost () | $500,000 | $500,000 |
| Expected Percentage Loss | 100% (If 100 drivers cost \5 on average) | |
| Observed Deviation (Worst Case Scenario) | \1,500,000 (One major loss) | \5,500,000 (One major loss event, but this is an outlier) | |
| Average Loss in Worst Case | 1,500% of expected cost | 110% of expected cost |
In the small sample, the one bad outcome ($1.5$ million dollars) results in a $1,500%$ deviation from the small expected aggregate cost, making financial planning nearly impossible. In the large sample, the same $1.5$ million dollar event is just an anomaly; the average loss across all 100,000 drivers remains extremely close to the calculated population mean, allowing the insurer to confidently set premiums that ensure long-term profitability.
This same principle underpins casino profitability. Every game, from roulette to slot machines, has a small house edge built in, meaning the expected return favors the house slightly. In a few spins or hands, a gambler might win big due to luck. Yet, over millions of calculated wagers, the total payout will converge to that small expected percentage loss for the player, guaranteeing the casino's profit margin.
# Computational Power
Beyond finance and risk, the LLN is fundamental to modern computation, especially in the Monte Carlo method. This simulation technique relies on repeated random sampling to approximate numerical results for problems that are otherwise too complex or impossible to solve analytically, such as complex integrals. The core instruction is simple: generate a massive number of random inputs based on the problem's parameters, calculate the result for each, and then average them. The LLN guarantees that the more trials you run, the closer your computed average gets to the true, sought-after value. If you are trying to approximate a definite integral, the accuracy of your final numerical answer directly tracks the number of samples you feed into the process, in line with the convergence theorems.
# The Business Context Versus Statistics
A common source of confusion arises when the term "law of large numbers" is used colloquially in business or finance to describe growth phenomena. In this non-statistical context, it suggests that companies achieving very high growth rates (like doubling revenue year-over-year) will inevitably see that percentage rate slow down as the underlying base dollar amount becomes enormous.
If a startup grows revenue from \1 million to \2 million (a $100%$ increase), that's achievable. Growing from \100 billion to \200 billion (still $100%$) requires adding a trillion dollars in market value in a single year, which becomes economically implausible under normal conditions. While this concept often reflects real-world phenomena like diminishing returns or economies of scale, it is technically distinct from the rigorous mathematical statement concerning the convergence of sample means from random variables. A company can theoretically maintain exponential growth, but the probability of doing so, when measured against the entire history of commerce, approaches zero—hence the common, if imprecise, reference to the law of large numbers.
# Boundaries of the Law
While extraordinarily powerful, the Law of Large Numbers is not universally applicable, and knowing its limitations is as important as understanding its strengths. The law requires the expected value () to exist and be finite.
If the underlying distribution is "heavy-tailed," such as the Cauchy distribution, the average will not converge to a single finite value, even as approaches infinity. In such distributions, extreme values are far more common than in distributions like the normal curve, meaning the sample mean keeps getting pulled around by massive outliers indefinitely, preventing convergence.
Furthermore, the law is built on the premise of independent and identically distributed trials. If the data collection process introduces selection bias—where the sample is systematically unrepresentative due to the way it was chosen—the law cannot correct for it. A survey that only contacts wealthy people will yield an average income skewed by that initial selection, no matter how many people are eventually included in the final, biased sample. The law refines the average of the sample towards the average of the population it represents, but if the representation itself is flawed from the start, the result will only confidently converge to the wrong number.
For researchers and analysts, the LLN sets a minimum expectation for data collection: it dictates that consistency in estimation is achieved not by perfect methodology on a few points, but by sheer volume that drowns out irreducible randomness. The strong and weak forms give us the mathematical assurance that this long-term stability is not merely wishful thinking, but a mathematical certainty under the right conditions.
Related Questions
#Citations
Law of large numbers - Wikipedia
7.1.1 Law of Large Numbers - Probability Course
Law of Large Numbers: What It Is, How It's Used, and Examples
Law of Large Numbers: Definition, Examples, and Use Cases
Law of Large Numbers -- from Wolfram MathWorld
What Is the Law of Large Numbers? (Definition) | Built In


