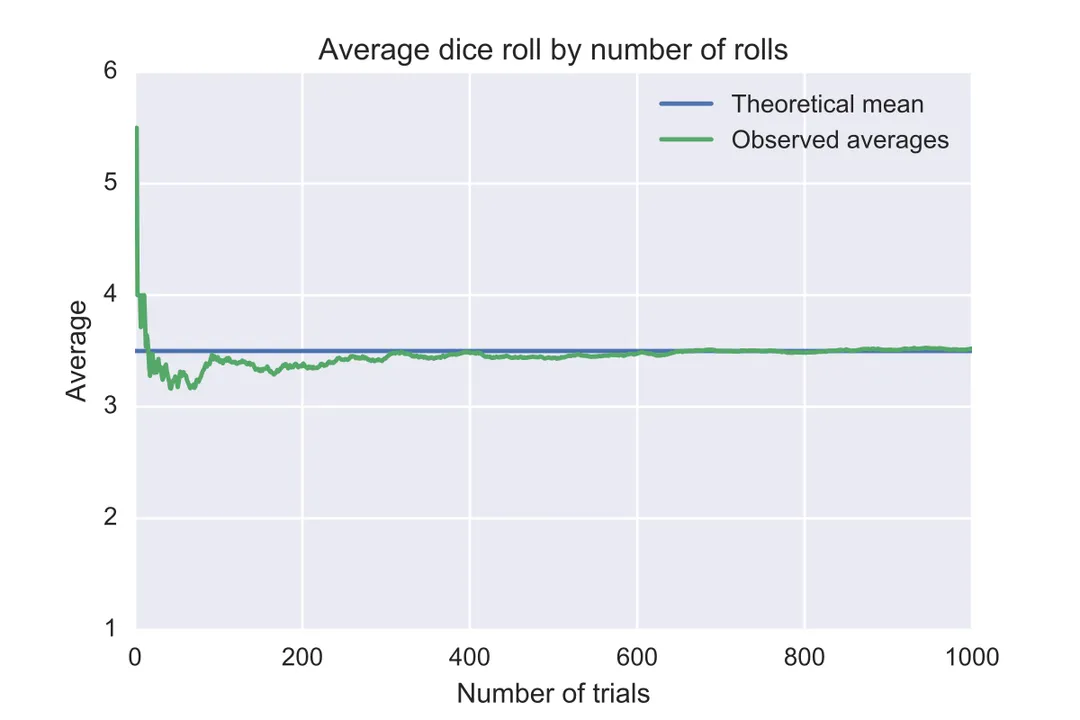
Under which condition regarding the underlying distribution will the sample mean *not* converge to a single finite value according to the LLN?
Answer
If the distribution is heavy-tailed, like the Cauchy distribution.
The law requires the expected value ($\mu$) to exist and be finite. If the distribution is heavy-tailed, such as the Cauchy distribution, extreme values occur often enough that the sample mean keeps getting pulled around indefinitely, preventing convergence to a single finite value.
Related Questions
What does the Law of Large Numbers formally dictate regarding the average of outcomes?What type of random variables is the formal definition of the LLN based upon?How does the variance of the sample average, $\text{Var}(\bar{X}_n)$, change relative to the sample size ($n$)?What mode of convergence does the Weak Law of Large Numbers (WLLN) guarantee?What does the Strong Law of Large Numbers (SLLN) assert about the sequence of sample averages?Which statement accurately describes the mathematical relationship between the Strong Law and the Weak Law?What specific notion does the Gambler's Fallacy incorrectly suggest regarding random events?What does the LLN smooth out regarding the observed results of a fair coin flip over many trials?How does the LLN benefit an insurance company dealing with individual policyholders?Under which condition regarding the underlying distribution will the sample mean *not* converge to a single finite value according to the LLN?If a data collection process introduces selection bias, what effect does the LLN have on the resulting average income calculation?