How does cosmic inflation explain large-scale uniformity?

The universe, when viewed on the grandest scales, presents an almost eerie level of order. If we look at the Cosmic Microwave Background (CMB)—the faint afterglow of the Big Bang—the temperature measured in every direction is virtually the same, differing by only about one part in $100,000$. [1][5] This astonishing large-scale uniformity is a fundamental observation about our cosmos, yet it poses a serious challenge to the standard, non-inflationary Big Bang model. How did regions of the early universe that appeared completely disconnected later manage to settle on the exact same temperature? Cosmic inflation, a theory proposing a brief but cataclysmic period of exponential expansion in the first fraction of a second after time began, provides the leading theoretical answer to this puzzle. [2][4][6][7][9]
# Uniformity Puzzle
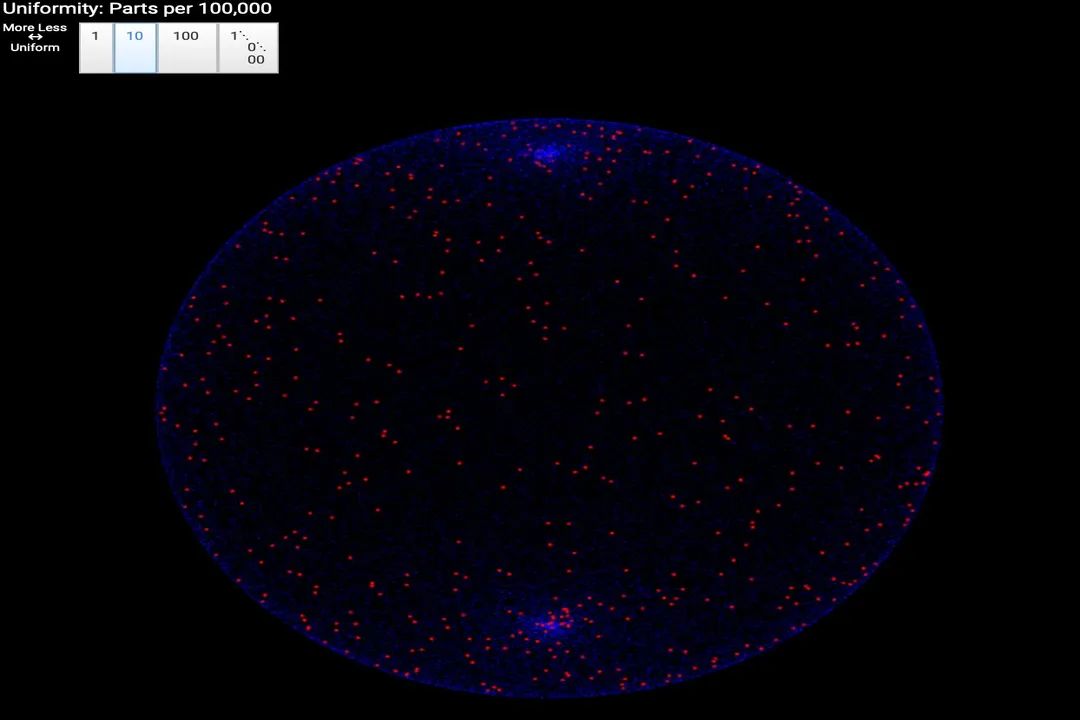
The core issue that inflation addresses is rooted in causal connection, often explained through two main problems: the horizon problem and the flatness problem. [1][5] To appreciate inflation's success, we first need to understand the nature of these challenges in the context of the Big Bang theory without the inflationary epoch.
# Horizon Difficulty
The universe, as we observe it today, is about $13.8$ billion years old. The CMB radiation we see originated when the universe was only about $380,000$ years old. [3] In the standard model, light (and thus information) can only travel a distance equal to the age of the universe multiplied by the speed of light. This distance defines the horizon—the boundary of what could have causally interacted with a given point. [1][5] When we measure the CMB, we see two opposite points on the sky that have never had time to exchange light or energy, meaning they were causally disconnected when the radiation was emitted. [1][5]
Yet, these causally disconnected patches share the same temperature. If they could never communicate, what mechanism guaranteed that they would reach thermal equilibrium independently to the same precise value? The standard model offered no satisfactory explanation for this shared starting condition. [1][3] It is like finding two widely separated puddles of water that evaporated at the exact same time, reaching the precise same ambient temperature, despite never having been connected by a river or stream. [5]
# Flatness Predicament
The second major puzzle relates to the geometry of spacetime, often quantified by the density parameter, . [1][5] General relativity suggests that the universe can have three primary geometries: closed (like a sphere, ), open (like a saddle, ), or flat (Euclidean, ). [1][5] Observations show that our universe is extremely close to flat today. [5]
For the universe to be this close to perfectly flat now, it must have been extraordinarily close to flat at the earliest moments of its existence. If deviated from $1$ by even a tiny amount in the first second after the Big Bang—say, $1.0000000000000001$—the expansion would have caused that deviation to grow so rapidly that the universe would have either immediately collapsed in on itself or expanded so quickly that structure formation would have been impossible. [1][5] The near-perfect flatness observed today thus demands an incredible fine-tuning of the initial conditions, a situation cosmologists generally find unsettling. [5]
# Inflationary Mechanism
Cosmic inflation posits that immediately following the Big Bang, perhaps around seconds, the universe underwent a phase of accelerated, exponential expansion driven by a hypothesized energy field known as the inflaton field. [2][4][7] This expansion was not just fast; it was exponentially fast, stretching spacetime by a factor of at least in a minuscule fraction of a second. [5]
# Exponential Stretch
The key difference between the standard Big Bang expansion and inflation is the rate of expansion. [6] While the universe has expanded continually since the Big Bang, inflation was a brief period where this expansion far outpaced the standard model’s predictions. [2][4][7] The driving force behind this was a temporary negative pressure generated by the vacuum energy associated with the inflaton field. [6]
Imagine a tiny, perfectly spherical grape, smaller than a proton, containing all the energy and matter of the observable universe today. During inflation, this region expanded so rapidly that in less than a trillionth of a trillionth of a trillionth of a second, it grew larger than our current observable universe. [4][5] This dramatic scaling process is central to resolving the uniformity problems. [2][4]
# Horizon Fix
Inflation directly resolves the horizon problem by postulating that the entire region that became our observable universe originated from an incredibly small, causally connected patch before inflation began. [1][5]
# Initial Contact
Before this period of rapid expansion, the universe was much smaller than the horizon size we calculate for the time the CMB was released. [5] In this earlier, smaller state, all parts of the region that would later form our observable universe were in causal contact, allowing them to exchange energy and achieve a uniform thermal equilibrium. [1][3] They could "talk" to each other.
# Stretching the Uniformity
Once this initial equilibrium was established, inflation kicked in, rapidly stretching that single, uniform patch of spacetime to enormous scales. [4][5] The immense stretching carried the initial smoothness across vast distances, far exceeding the current cosmic horizon. [1] When inflation ended, the universe that emerged was large, smooth, and uniform across every region now visible to us. [5] The reason we see the same temperature everywhere is not because distant regions communicated after the CMB formed, but because they were all once neighbors before inflation separated them. [1][3]
This mechanism elegantly explains why the CMB is isotropic (the same in all directions). [5] It turns a problem of synchronicity across vast distances into a problem of origin within a tiny, pre-inflationary region. If the initial patch was uniform, stretching it preserves that uniformity across the newly formed, much larger volume. [1]
# Geometry Balance
Inflation also offers a powerful explanation for the observed flatness of the universe without invoking extreme fine-tuning. [1][5]
# Flattening Effect
Consider the analogy of blowing up a balloon. [5] If you draw a small, curved triangle on the surface of a deflated balloon, and then inflate it to an enormous size, the triangle will appear increasingly flat to any observer standing on its surface. [1] The intense, superluminal stretching characteristic of inflation acts like this inflation of the balloon surface. [5]
The exponential expansion drives the spatial geometry toward flatness () regardless of its initial curvature. [1][5] If the universe started slightly closed (), inflation stretched it so dramatically that any initial curvature is effectively diluted to the point of being unmeasurable today. [5] The expansion is so powerful that it pushes the density parameter relentlessly toward unity. This means that the near-perfect flatness we measure today () is a natural consequence of inflation, rather than a cosmological coincidence requiring specific initial settings. [5] The factor of expansion required is so large—a minimum of —that it renders any initial deviation from flatness negligible. [1][5]
To illustrate the scale involved, consider that the observable universe today spans about $93$ billion light-years across. If inflation occurred, the pre-inflationary region we came from was microscopic, far smaller than the scale of a single subatomic particle, yet it contained the seeds of everything we see, smoothed to perfect uniformity before the stretch began. [4]
# Structure Emergence
A theory explaining uniformity must also explain the lack of perfect uniformity, because the universe is not perfectly smooth; it contains galaxies, clusters, and voids. [2] Inflation explains this apparent contradiction by turning microscopic quantum jitters into the seeds of cosmic structure. [4][5]
# Quantum Seeds
In the tiny, causally connected patch before inflation, quantum mechanics dictated that energy density could not be perfectly zero everywhere; there were unavoidable, tiny quantum fluctuations inherent to the field. [2][5] These fluctuations are random variations in the energy density across the patch. [4]
During the rapid inflationary expansion, these microscopic, subatomic fluctuations were stretched across cosmological distances. [2][4] As they were stretched, they effectively exited the quantum realm and became classical density perturbations imprinted on the overall spacetime fabric. [5] Regions that were infinitesimally denser than average were stretched into slightly larger regions of over-density, and vice versa. [2]
# Seeding Galaxies
When inflation ended and the universe began its slower, standard expansion, these stretched, classical density variations acted as the initial seeds for gravitational collapse. [4][5] Over billions of years, gravity amplified these slight over-densities, drawing in surrounding matter until they formed the first stars, galaxies, and the vast cosmic web we map today. [2] The uniformity observed in the CMB represents the baseline smoothness before these tiny quantum seeds were stretched and amplified, while the structure we see now is the direct result of those same seeds. [5] The characteristic pattern of these fluctuations is, remarkably, consistent with the predictions of the theory. [4]
# Comparing Models
The stark contrast between the standard Big Bang model and the inflationary extension highlights why inflation is so strongly supported by observational data, particularly regarding uniformity. [9]
| Feature | Standard Big Bang (Pre-Inflation) | Inflationary Model | Implication for Uniformity |
|---|---|---|---|
| Initial State | Requires pre-existing uniformity across causally disconnected regions | Explains uniformity via an initial, tiny, causally connected region | Solves the Horizon Problem [1][5] |
| Geometry () | Requires precise fine-tuning near from the start | Drives the geometry toward naturally during expansion | Solves the Flatness Problem [1][5] |
| Origin of Structure | Structure must arise from unknown initial conditions or instabilities | Structure arises from stretched, amplified quantum fluctuations | Explains structure growth from uniformity [2][4] |
The beauty of inflation is that it solves multiple deep puzzles with a single mechanism based on fundamental physics principles, namely an early period of exponential expansion driven by a scalar field. [9] Furthermore, the theory makes specific predictions about the statistical properties of the initial fluctuations that created structure, predictions which have been largely confirmed by precise measurements of the CMB. [2][4]
This predictive power elevates inflation from a mere patch to a genuine extension of cosmology. An interesting comparison arises when we consider the time scale of the uniformity mechanism versus the time scale of structure formation. Uniformity is established within the first seconds or so, dictated by the duration of the exponential stretch. [7] Structure formation, however, takes the next $13$ billion years to fully manifest via gravitational clumping. It is a profound thought that the smoothness of the entire visible cosmos was set in stone before the universe was even a single picosecond old, while the intricate details we study today are merely the result of that initial smoothness being slightly perturbed and then magnified over eons. [2] This shows a clean separation of scales in cosmic history: the first moment sets the stage for temperature, and the subsequent billions of years play out the drama of gravitational aggregation.
#Videos
Cosmic Inflation Explained | Cosmology 101 Episode 6 - YouTube
Related Questions
#Citations
Why is cosmic inflation required to explain the uniformity of the CMB?
Cosmic inflation - Wikipedia
Inflation in the Universe - Cosmic Times - NASA
Uniformity And Uniqueness Of The Universe - Edge.org
3.3 Large-scale Uniformity - World Science U
Cosmological Inflation Theory: Explaining the Early Universe
Cosmic Inflation Explained | Cosmology 101 Episode 6 - YouTube
[PDF] Inflation and the New Era of High-Precision Cosmology | MIT Physics
Cosmic Inflation Theory and the Uniformity Problem - Shortform Books

