What role do models play in scientific prediction?

Scientific models serve as indispensable intermediaries between the messy complexity of the real world and the structured abstraction required for rigorous scientific inquiry. [2][7] They are, fundamentally, simplified representations of reality, constructed for a specific purpose, which most often involves explaining phenomena or making predictions about future or unobserved states. [1] When a scientist seeks to understand something too large, too small, too fast, or too intricate to observe directly, a model steps in to bridge that gap. [4][6] The prediction is the payoff; it is the concrete test of whether the model accurately captures the relevant mechanisms of the system under study. [8]
The act of creating a model necessitates idealization and abstraction. [1] This means that the model intentionally omits details that the constructor deems irrelevant to the question at hand, focusing only on the core relationships. A weather model, for instance, does not track every molecule of air on Earth; rather, it focuses on fluid dynamics, thermodynamics, and boundary conditions. If these assumptions—the scaffolding upon which the model rests—are flawed or incomplete, the resulting predictions, however mathematically elegant, will fail to match reality. [5] Therefore, the role of the model in prediction is not just about calculation; it is about representation and the careful management of what we choose to ignore. [1]
# Model Varieties
Models manifest in several distinct forms, each carrying different strengths for predictive tasks. [2] Understanding these differences helps clarify what kind of prediction we can expect from a given scientific endeavor.
# Physical Forms
Physical models are tangible, scaled-down or scaled-up replicas of the real system. [7] Think of a scale model of an airplane wing tested in a wind tunnel, or a topographical map representing terrain. [2] Their predictive value often comes from observing how the scaled system behaves under controlled conditions that mimic the real environment. [4] While excellent for visualizing structures and testing basic mechanical interactions, their predictive reach is often limited to the specific physical parameters they can replicate accurately. They cannot easily predict fundamentally different states, like an entirely new atmospheric event or a change in fundamental physical constants. [1]
# Conceptual Structures
Conceptual models are built from ideas, analogies, and diagrams that structure scientific understanding. [7] In biology, the model of DNA as a double helix is a conceptual structure that allows scientists to predict how genetic information is copied and inherited. [2] These models are powerful for organizing knowledge and suggesting new avenues of investigation. Their predictions tend to be qualitative or schematic—suggesting that a process will occur or how two variables relate—rather than providing precise numerical outcomes. [4]
# Mathematical Constructs
The most frequently associated models in modern science are the mathematical or computational ones. [2] These models use equations, algorithms, and data to describe system dynamics, allowing for precise quantitative prediction through simulation. [6] Climate models, epidemiological spread models, and gravitational simulations fall into this category. [5] These are the workhorses of forecasting because, given the correct initial conditions and parameters, they can generate specific, testable outcomes. [8] The predictive power here is directly tied to the fidelity of the underlying mathematical relationships to the physical or biological laws governing the system. [1]
| Model Type | Primary Output | Predictive Strength | Key Limitation |
|---|---|---|---|
| Physical | Observable Behavior | Direct, analogical results | Limited to reproducible physical scales/conditions [1][4] |
| Conceptual | Diagrams, Relationships | Guiding hypotheses, qualitative structure | Lacks numerical precision [7] |
| Mathematical | Numerical Values, Simulations | Quantitative forecasting across time/space [6] | High reliance on initial conditions and assumptions [5] |
# Generating Forecasts
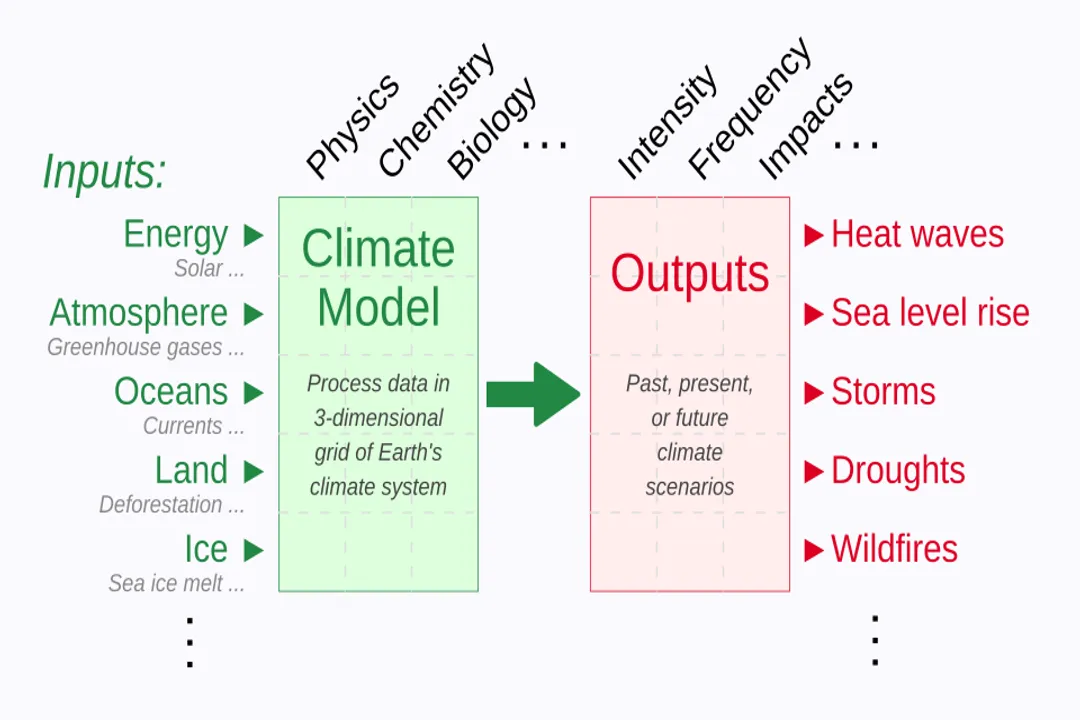
The process of using a model to generate a prediction is distinct from simply explaining a past observation, though the two are deeply intertwined. [7] An explanation shows why something happened based on the model’s internal logic; a prediction shows what will happen if those same internal logics are followed into the future or applied to new data. [3]
For computational models, prediction involves initializing the system with current or past data (the initial conditions) and then running the equations forward through time. [6] This is especially evident in areas like meteorology, where models assimilate vast amounts of current atmospheric readings to project conditions hours or days out. [5]
A key distinction arises when discussing prediction versus forecasting in some scientific contexts. [8] While the terms are often used interchangeably, some literature distinguishes between a true prediction—an outcome far outside the range of directly observed data, often involving novel mechanisms—and a forecast, which is an extrapolation within or near the bounds of existing data, relying on established, well-verified relationships. [8] For example, predicting the exact orbital path of a newly discovered asteroid decades from now is a mathematical forecast based on well-understood Newtonian mechanics. Predicting the long-term evolutionary path of a complex ecological system over millennia involves far greater uncertainty because the underlying 'laws' are statistical and subject to emergent, unpredictable factors. [9]
One important aspect often overlooked when evaluating predictive models is the "window of reliability." A model might be incredibly accurate for the first two time steps (e.g., predicting weather for the next 24 hours) but rapidly lose fidelity thereafter. [5] This decay rate is intrinsically linked to the inherent sensitivity of the system being modeled. A simple pendulum has a very wide window of reliability; a chaotic system like atmospheric convection has a very narrow one. Scientists must always report predictions alongside a measure of this window, effectively stating, "This prediction holds true provided the system behaves according to the known dynamics for this specific duration". This discipline moves the practice away from magic and toward verifiable science.
# Assessing Model Worth
A model is only as good as its ability to accurately represent the system it is meant to mimic, which requires constant validation. [3] Since models are inherently simplifications, we must judge them not on whether they are perfectly true—they never are—but on whether they are fit for purpose. [1]
# Calibration and Verification
Before any prediction is trusted, the model must be rigorously tested against historical data—a process often involving calibration and verification. [5] Calibration involves tuning the model's internal parameters so that its output matches known historical observations. Verification then confirms that the calibrated model can accurately reproduce data it was not explicitly tuned against. If a model calibrated on the climate data of the 20th century can accurately predict known temperature anomalies from the early 1900s, its predictive framework gains credibility.
However, one must guard against overfitting. This occurs when a model becomes so intricately tailored to the existing dataset—including its noise and specific idiosyncrasies—that it loses its generalizability. [3] An overfit model performs perfectly on past data but generates wildly inaccurate predictions when faced with new, unseen inputs. It mistakes noise for signal. Recognizing overfitting requires testing the model on several independent datasets or employing techniques that penalize complexity, such as using simpler models when they achieve comparable accuracy to highly complex ones. [1][5]
# Uncertainty Quantification
A crucial element missing from many public discussions of scientific prediction is the explicit quantification of uncertainty. [9] In the most sophisticated modeling efforts, especially in fields like risk assessment or climate science, the output is not a single number but a distribution of possibilities. [5][9] For instance, instead of predicting a sea-level rise of 'X' centimeters by 2100, the model might predict a 90% chance that the rise will fall between 'Y' and 'Z' centimeters. This probabilistic approach acknowledges the inherent limitations imposed by incomplete knowledge and measurement error. [1] Policymakers must understand that the 'best guess' is often the mean of a wide distribution, and the tails of that distribution represent significant, albeit less probable, risks. [9]
# Predicting Complexity

The role of models shifts depending on the complexity and chaos inherent in the system being studied. The predictive success seen in classical physics, based on deterministic, linear systems, sets a high bar that many other sciences struggle to meet. [1]
In complex systems—those involving many interacting components where small initial changes can lead to vastly different outcomes—the predictive task changes from forecasting specific events to modeling the range of possibilities or identifying tipping points. [9] Consider the modeling of financial markets. While some fundamental economic principles can be modeled, the sheer volume of independent, sometimes irrational, human decisions makes precise, long-term prediction virtually impossible. Models in these fields are thus often used more to understand systemic vulnerabilities—what kind of shock could cause a collapse?—than to predict when a collapse will occur. [3]
A helpful way to categorize predictive models, which often dictates their reliability, is by looking at the state space they explore. If a model is asked to predict within its interpolation zone (predicting values between known data points), accuracy is generally high. If it must predict far outside this zone (extrapolation), the model is relying entirely on its assumed physical laws holding true under never-before-seen conditions, which significantly increases the risk of error. [8] For instance, predicting the next solar flare based on historical patterns is interpolation; predicting the long-term effects of solar activity on a terraformed Mars atmosphere is extreme extrapolation.
# Interpretation and Choice
The final layer of the model’s role in prediction involves the human scientist making a judgment call. When multiple competing models exist—perhaps one is mathematically simpler (more parsimonious) but another incorporates more variables—the scientist must choose which best serves the immediate predictive goal. [1][3] There is no universal metric for this choice; it depends on the required accuracy, the acceptable error margin, the time horizon, and the computational resources available. [5]
A scientist applying this knowledge practically might develop a layered validation checklist before issuing a major forecast.
- Assumption Audit: List every major idealization made (e.g., "assumed frictionless surface," "assumed constant population growth rate"). Are these assumptions justifiable for the prediction window?
- Sensitivity Testing: Rerun the model by deliberately perturbing the top three most influential input parameters. If the output changes drastically with minor input changes, the prediction should be flagged as highly sensitive and perhaps unreliable. [9]
- Cross-Model Comparison: If an independent model (built on different assumptions or mathematical techniques) yields similar results, confidence increases significantly, even if both models are technically imperfect.
This interpretive stage underscores that the model is a tool, not an oracle. The expertise lies not just in building the tool but in understanding its limits when applying its output to real-world prediction. [4][9] The scientific model, therefore, plays the role of a constrained imagination—it allows us to mentally simulate futures we cannot yet observe, but it requires constant calibration against the reality that is observable now.
Related Questions
#Citations
Models in Science - Stanford Encyclopedia of Philosophy
Scientific modelling - Wikipedia
Why Are Scientific Models Important in the Study of Science?
What is meant by engaging youth in scientific modeling?
Why Models are Advantageous to Learning Science - ScienceDirect
The Power of Scientific Modeling in Science Education - Gizmos
Understanding Scientific Models: A Comprehensive Guide for 2024
Can Models Predict the Future? - FEWscapes
[PDF] The Role of Models in Prediction for Decision

