What causes phase transitions?

The sudden transformation of a substance from one physical state to another—ice melting into water, or water boiling into steam—is a phenomenon we see daily, yet the root cause is a deep interplay of energy, entropy, and collective behavior. A phase transition, fundamentally, is an abrupt, discontinuous change in the defining physical properties of a medium as an external condition, like temperature or pressure, is varied smoothly. The key question isn't where the transition happens, but why the system suddenly commits to a completely different way of organizing itself.

# Free Energy Minimum

The driving mechanism behind any phase transition lies in the search for the state of minimum free energy. For a system held at constant temperature ( $T$ ) and pressure ( $P$ ), this is the Gibbs free energy ( $G$ ). A system naturally seeks the configuration—solid, liquid, or gas—that minimizes $G = E - T S$ , where $E$ is the internal energy, and $S$ is the entropy.

For familiar changes like the liquid-gas transition, the system exists in equilibrium only when the Gibbs free energy per particle ( $μ \mu$ or $g$ ) is identical for both phases present. If the external conditions shift such that $G_{\text{liquid}} > G_{\text{gas}}$ , the system will spontaneously reorganize to maximize the proportion of gas.

This competition is often framed as a battle between energy and entropy:

Energy ( $E$ ): Lower energy states typically correspond to more ordered arrangements where attractive forces between particles are satisfied. For water freezing to ice, the crystalline structure holds molecules rigidly, maximizing favorable intermolecular bonds, thus minimizing potential energy.
Entropy ( $S$ ): Entropy measures the number of accessible microstates. Highly disordered phases, like gas, have vastly higher entropy because molecules have more freedom of movement and spatial arrangement.

At very low temperatures, the $T S$ term is small, so energy dictates the stable phase, favoring the ordered, low-energy solid. As temperature increases, the entropy term ( $T S$ ) becomes more significant, eventually tipping the balance so that the higher-entropy liquid or gas phase becomes the new minimum of the free energy, causing the transition.

# Latent Heat and Discontinuities

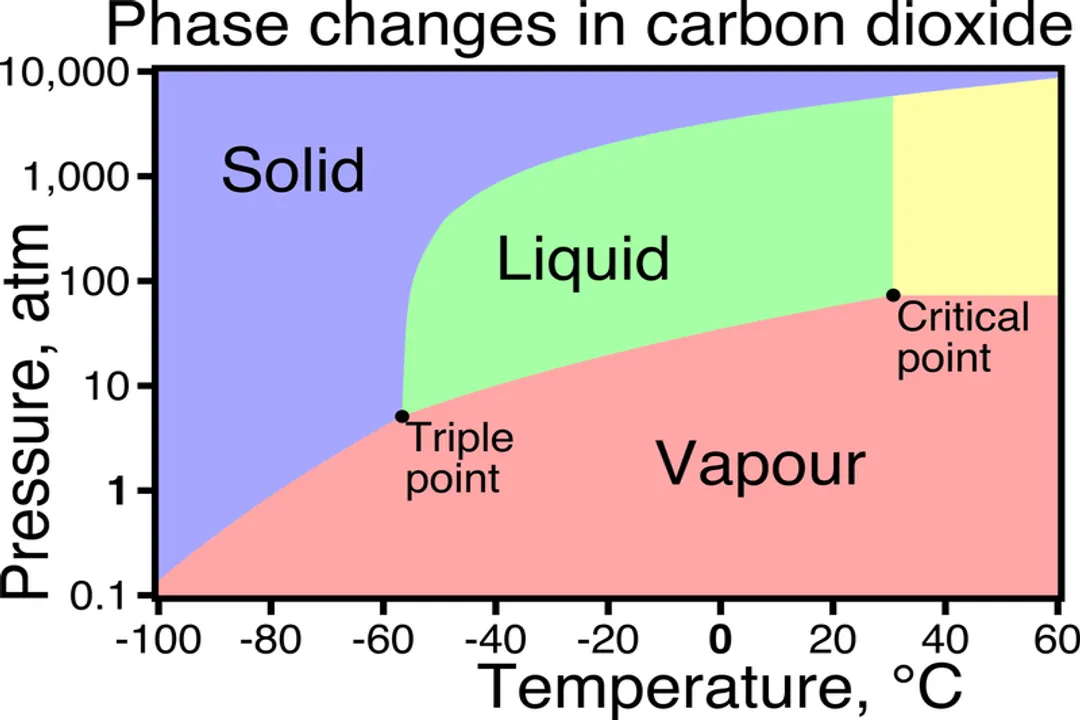
When this change is of the first order, it involves a discontinuous jump in a thermodynamic quantity, most notably the density/volume, and is characterized by the exchange of latent heat. Latent heat is the energy absorbed or released during the transition without any accompanying temperature change. For example, while boiling water, adding heat supplies the latent heat of vaporization, which breaks the remaining liquid-phase intermolecular bonds, even though the temperature holds steady at the boiling point until all the liquid is gone.

The path along which these first-order transitions occur in the pressure-temperature ( $P - T$ ) plane is governed by the Clausius-Clapeyron equation. This equation relates the slope of the coexistence curve ( $\text{d}P/\text{d}T$ ) to the latent heat ( $L$ ) and the discontinuity in volume ( $\Delta v$ ) between the phases:

$\frac{\text{d}P}{\text{d}T} = \frac{L}{T(\Delta v)}$

This mathematically captures the essence: the slope of the line separating the phases depends on how much energy is stored/released during the change and how much the volume changes when crossing that boundary.

What causes signal attenuation in circuits?

# Order and Symmetry

To categorize transitions beyond the simple solid-liquid-gas changes, physicists look for an order parameter. This is a macroscopic quantity that is zero in the disordered phase (usually high temperature) and non-zero in the ordered phase (low temperature). For a ferromagnet, this is the net magnetization ( $M$ ); for the liquid-gas transition, it is the difference in density ( $\Delta\rho$ ).

The transition is frequently associated with spontaneous symmetry breaking. The high-temperature state (like a liquid) possesses high symmetry—there is no preferred direction or location, as molecules are randomly arranged. When the system cools below a critical temperature ( $T_{c}$ ) and orders (e.g., into a crystal or a ferromagnet), it must "choose" one of several equivalent ordered ground states (e.g., magnetizing up or down). This choice breaks the underlying symmetry of the governing equations, leading to a state with lower symmetry. For instance, in a ferromagnet, the system picks a preferred magnetic direction, breaking the rotational symmetry that existed when all directions were equally likely at high temperatures.

A crucial observation here is the difference between liquid-gas and magnetic transitions. The liquid and gas phases have the same symmetry group, allowing a continuous path between them that ends at the critical point, where the two phases become indistinguishable (a supercritical fluid). Solid-liquid transitions, however, always involve a change in symmetry (breaking lattice translation symmetry), so they must always be separated by a first-order transition line that continues indefinitely on the phase diagram.

# Second Order Behavior and Fluctuations

When the symmetry change is subtle, we encounter second-order or continuous phase transitions. Here, the order parameter changes smoothly to zero at $T_{c}$ , but a thermodynamic response function—like heat capacity or magnetic susceptibility—diverges. This continuous vanishing of the order parameter indicates that the system is no longer crossing a barrier, but rather that the $m = 0$ solution of the free energy begins to become unstable against small fluctuations.

This critical region is where classical equations of state, like the van der Waals equation for gases or Mean Field Theory (MFT) for magnetism, break down because they only rely on average properties.

The real cause for the breakdown of simple models near $T_{c}$ is enhanced fluctuation. As density fluctuations approach the critical point, the compressibility diverges, meaning the system is simultaneously exploring densities both above and below the average. This massive change in local configuration is missed entirely by equations that only use the system's average density or magnetization. This leads to a profound physical result known as universality: the mathematical description, governed by critical exponents that describe the power-law approach to $T_{c}$ , is identical across vastly different systems (e.g., liquid-gas vs. 3D Ising magnets). The messy microscopic details are irrelevant near the critical point; only the dimensionality and the symmetry of the order parameter matter.

To understand how these spatial variations influence the transition, a more sophisticated model like Landau-Ginzburg theory is necessary. This approach introduces a free energy functional $F[m(\mathbf{r})]$ that depends on the order parameter $m$ varying in space, incorporating an energy cost for spatial variation (the gradient term).

What causes autoimmune disorders?

# The Suppression of Order

Fluctuations are not always a feature that accompanies a transition; sometimes, they are the mechanism that prevents it entirely. The success of ordering depends critically on the spatial dimension ( $d$ ).

Consider the magnetic ordering in the Ising model. In $d = 1$ (a simple chain of spins), the energy required to create a defect—a region of flipped spins—scales only with the perimeter (two endpoints, $E \propto L$ ) of the defect, while the entropy scales with its length ( $L$ ) because the defect can exist anywhere along the chain. Since the free energy of creating a droplet scales as $F \propto E - TS \propto \text{constant} - T \log N$ , for any temperature $T>0$ , the system can always find a lower free energy by creating infinitely long, disordered regions. Thus, thermal fluctuations completely destroy the ordered phase in one dimension, meaning no phase transition occurs above absolute zero, a result MFT incorrectly predicts.

In contrast, in $d = 2$ and $d = 3$ , the energy cost to create a domain scales with its perimeter, which grows faster than the logarithm of the available volume, allowing the ordered phase to win out at sufficiently low temperatures. This dimensionality dependence is a direct consequence of the mechanism driving the transition: the geometry of the energy barrier relative to thermal noise.

This reveals a core principle: what causes a phase transition is the thermodynamic drive to reach the lowest free energy state, but the nature of that transition (first-order jump, continuous vanishing, or complete suppression) is dictated by the geometry of the energy landscape and the magnitude of fluctuations, which are highly dependent on the system’s dimensionality.