What causes resonance amplification?

The phenomenon we call resonance amplification is one of the most counter-intuitive yet fundamentally important concepts in physics, manifesting in everything from the gentle hum of a stringed instrument to the catastrophic failure of large structures. At its simplest, resonance occurs when a system, which naturally oscillates at a certain pace, is driven by an external force that pushes it at that exact same pace. This precise timing between the external push and the system's natural rhythm causes the amplitude of the system’s motion—its swing or vibration—to grow dramatically, far beyond what the external force alone would suggest. ^[2]^[4]^[5] The core cause of this dramatic amplification is the constructive addition of energy over successive cycles, perfectly aligned with the system's internal clock. ^[3]

# Natural Rhythm

To understand resonance, we must first grasp the idea of a system's natural frequency. Every physical object or assembly capable of vibrating possesses an inherent, preferred rate at which it will oscillate if disturbed and then allowed to move freely without any further external influence. ^[4]^[9] This internal frequency is dictated entirely by the object's physical properties—its mass, its stiffness, and its geometry. ^[4]

Consider a simple pendulum. Its natural frequency—how fast it swings back and forth—is determined primarily by the length of its string or rod. A shorter pendulum swings faster; a longer one swings slower. ^[1] This frequency is the system’s "default setting" for vibration. ^[4] For a guitar string, the tension and mass per unit length set this frequency, which we perceive as pitch. ^[1] In an electrical circuit composed only of an inductor ( $L$ ) and a capacitor ( $C$ ), the natural frequency is determined by the values of $L$ and $C$ . ^[2] This natural frequency, often denoted as $\omega_0$ , represents the rate at which the system is most efficient at exchanging energy between its potential and kinetic forms, or in an electrical sense, between electric and magnetic fields. ^[2]^[4]

# External Pushing

Resonance amplification only occurs when this natural frequency ( $\omega_0$ ) meets an external, periodic driving force whose frequency ( $\omega$ ) matches it precisely ( $\omega = \omega_0$ ). ^[4]^[9] If the external force is random or changes frequency constantly, the system might move a little, but it won't build up that characteristic, large-scale resonant response. ^[3]

Imagine pushing someone on a swing set. The swing has a natural period—the time it takes to complete one full back-and-forth cycle—which is set by the length of the chains. ^[1] If you push the rider randomly, or if you push when they are moving toward you (which would actively slow them down), you are inputting energy inefficiently. However, if you wait until the swing reaches its maximum height and begins moving away from you, and then apply a small, precisely timed push, you are adding a small packet of energy exactly when the swing is ready to accept it and begin its next outward arc. ^[1]^[4] This external periodic input, timed perfectly to the system's internal rhythm, is the direct causal requirement for resonance. ^[3]

What causes acoustic resonance?

# The Mechanism of Buildup

The reason this precise matching causes such a massive change in amplitude relates to the way energy is accumulated, often explained through the concept of constructive interference. ^[2]

When the driving frequency matches the natural frequency, every successive impulse from the external force arrives in phase with the existing motion of the system. ^[3] This means that the energy being added always reinforces the motion already underway, rather than opposing it. The energy doesn't just move the object once; it gets trapped momentarily, building up within the system's energy storage mechanisms (like potential energy in a stretched spring or kinetic energy in a fast-moving mass). ^[1]

In a purely theoretical, undamped system—one with absolutely no energy loss to friction or air resistance—this continuous, perfectly timed energy input would lead to an infinite amplitude of oscillation. ^[2] The system would just keep swinging higher and higher until it physically broke apart. ^[3] This is why the collapse of structures like the Tacoma Narrows Bridge, while often misattributed solely to wind, was a stark demonstration of energy accumulation at a resonant frequency causing amplitudes to exceed the structural limits. ^[6]

# The Essential Role of Damping

In the real world, infinite amplitude is impossible because every mechanical or electrical system experiences damping. ^[2] Damping represents all the processes that dissipate the system’s mechanical energy, usually as heat, into the environment. This includes air resistance, friction between moving parts, and internal molecular friction within the material itself. ^[2]

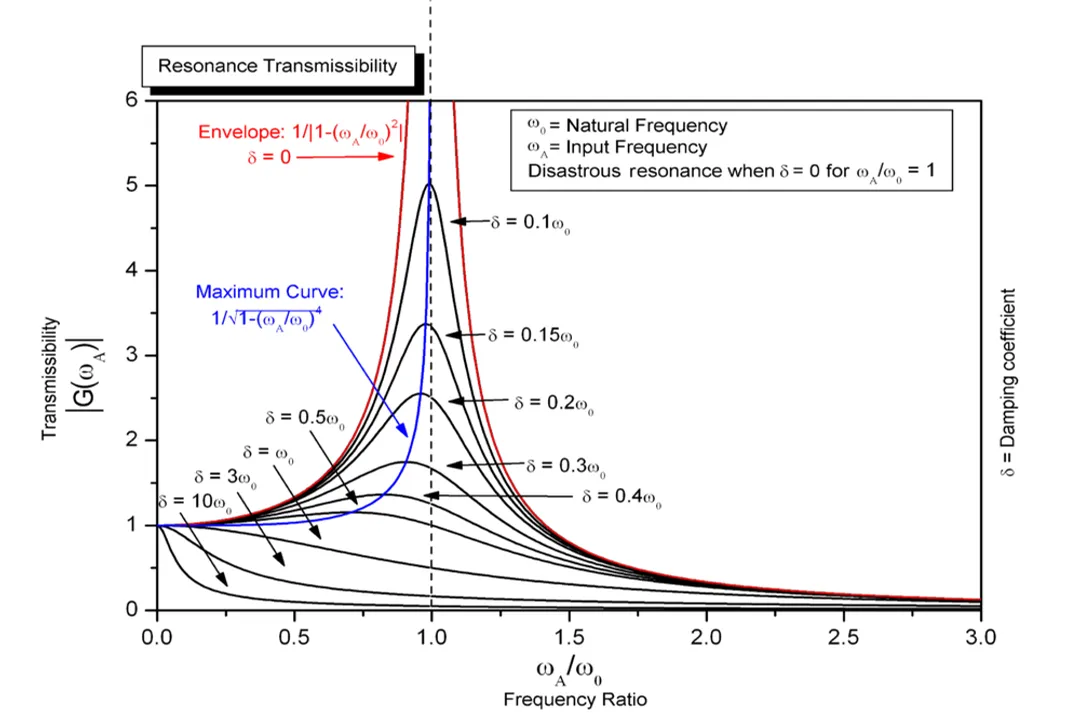
Damping acts as the critical governor on the resonant amplification. While the cause of the peak is the frequency match, the height of that peak is entirely determined by how little damping is present. ^[2]^[3]

Low Damping: Systems with very little damping—like a high-quality tuning fork or a delicate quartz crystal oscillator—will exhibit a very sharp, high peak in their response curve right at the natural frequency. A tiny amount of external energy can generate a huge amplitude. ^[2]
High Damping: Systems with significant damping—like a shock absorber in a car or a heavy pendulum swinging in water—will have a much broader, flatter resonance curve. Even when driven exactly at the natural frequency, the amplified amplitude will be relatively small because energy is continuously leaking out as fast as it is being put in. ^[2]

This relationship between damping and peak amplitude is an important characteristic. An engineering system might be designed to operate near a natural frequency but with enough damping built in (e.g., through rubber mounts or viscous fluids) to ensure that even if the driving frequency drifts slightly, or if the driving force unexpectedly increases, the resulting vibration amplitude remains manageable and safe. ^[6]

What causes autoimmune disorders?

# Frequency Matching Across Disciplines

The principle causing resonance amplification—the matching of driving frequency to natural frequency—is universal across different types of oscillatory systems. ^[7]

# Mechanical Systems

In mechanics, we deal with mass-spring systems, pendulums, and vibrating beams. ^[4] The natural frequency depends on stiffness and mass. Driving a system at this frequency causes large displacements. ^[9] For instance, the human body has several natural frequencies related to how different parts—the head, the torso, the limbs—respond to vibration. If a vehicle's engine or road surface introduces periodic vibrations that match one of these frequencies, the resulting oscillations felt by the passenger can become intensely uncomfortable or even physically damaging because the system is maximizing energy absorption at that specific rate. ^[6]

# Electrical Circuits

In electronics, resonance occurs in $L C$ circuits (combinations of inductors and capacitors). ^[2] The natural frequency of oscillation in such a circuit is fixed by the $L$ and $C$ values. When an external alternating current (AC) signal is applied at this precise frequency, the circuit's impedance—its opposition to the current—reaches a minimum (in a series $L C$ circuit) or maximum (in a parallel $L C$ circuit), leading to a massive amplification of the current or voltage at that specific frequency. ^[2] This phenomenon is the bedrock principle allowing a radio receiver to select one station's signal out of the multitude of waves bombarding its antenna; the radio is tuned so its $L C$ circuit resonates sharply to the desired station's carrier wave frequency, amplifying it selectively. ^[2]

# Sound and Waves

Resonance is fundamental to how we perceive and produce sound. ^[1] When a musician plucks a string, the string vibrates at its natural frequency, producing a faint sound. This vibration is transferred to the larger body of the instrument (like the wooden box of a violin or the air cavity of a flute). The instrument's body is designed to have natural frequencies that match the harmonics of the string. ^[1] When the frequencies match, the air inside the instrument is forced into resonance, rapidly accumulating vibrational energy, which is then efficiently radiated as loud sound waves into the room. ^[1] A common illustration involves two identical tuning forks; striking one causes the other, untouched fork to begin vibrating audibly because the sound waves from the first fork contain the exact frequency needed to drive the second fork into resonance. ^[2]

# Analyzing System Behavior

When trying to diagnose or design a system involving oscillations, recognizing the cause of amplification is key: is it resonance, or simply a powerful driving force?

A practical distinction arises when looking at how energy is managed. In a system experiencing resonance, the energy input is highly efficient due to the timing, leading to large amplitudes even from small external forces. ^[3] Contrast this with a case where a structure fails due to extreme wind loads that are simply too high across the board. In the latter case, the driving force itself is excessive. In the former, the driving force might be modest, but the system's inherent frequency provides the mechanism for massive energy concentration. ^[4]

One crucial aspect in engineering analysis is understanding that a physical object rarely vibrates in just one simple way. It has several modes of vibration, each with its own natural frequency. For example, a long bridge has a frequency associated with simple side-to-side swaying, another for vertical bending, and yet another for twisting. ^[6] If a steady vibration source—like traffic, wind eddies, or seismic activity—happens to match the frequency of the twisting mode, even if it doesn't match the swaying mode, the twisting amplitude will skyrocket. Recognizing and designing against all significant resonant modes is far more critical than just preventing the lowest-frequency mode from exciting. ^[6]

When we look at systems like acoustic spaces or electronic filters, we intentionally exploit this cause of amplification. We design cavities or circuits to have a very high Q-factor (Quality Factor), which is a measure related to low damping and high sharpness of the resonance peak. ^[2] A high Q-factor means the system is extremely sensitive to deviations from its target frequency but provides maximum gain right at that target. ^[2]

It is essential not to confuse the physical manifestation of resonance with the underlying physical cause. The high-amplitude swing is the effect; the frequency match between the driving force and the natural frequency is the cause. ^[3]^[4] If one were to simply increase the mass of the child on the swing, the natural frequency would change (it would swing slower). If the external pusher continued pushing at the old frequency, the resonance would disappear, and the amplitude would drop, even though the pusher is still applying force in the "right" direction. The cause of the amplification is inextricably linked to the specific physical properties ( $\omega_0$ ) of the object being driven. ^[4]

In summary, the cause of resonance amplification boils down to one fundamental condition: the frequency of the external periodic excitation must match the natural frequency of the oscillating system. ^[4]^[9] This perfect synchronization allows the external energy input to constructively interfere with the system's ongoing motion, leading to a sustained, dramatic increase in amplitude until the energy dissipated by damping balances the energy being added by the driving force. ^[2]^[3] This precise interplay between inherent properties and external timing is what makes resonance both a powerful tool in engineering and a force to be rigorously guarded against in structural design. ^[7]