How do scientists measure the Earth?

The desire to quantify our home world is ancient, rooted in the practical needs of navigation and the philosophical drive to understand scale. Before we had satellites orbiting overhead, pinning down the precise size and shape of the Earth was a monumental intellectual and physical challenge. It required keen observation, sharp geometry, and a willingness to travel great distances to take measurements. ^[6] The Earth is not a perfect sphere; it is an oblate spheroid, bulging slightly at the equator due to its rotation, a fact that has complicated measurement efforts throughout history. ^[3][8] Determining its dimensions—circumference, radius, and diameter—has evolved from shadow measurements to complex global positioning systems.

# Early Geometry

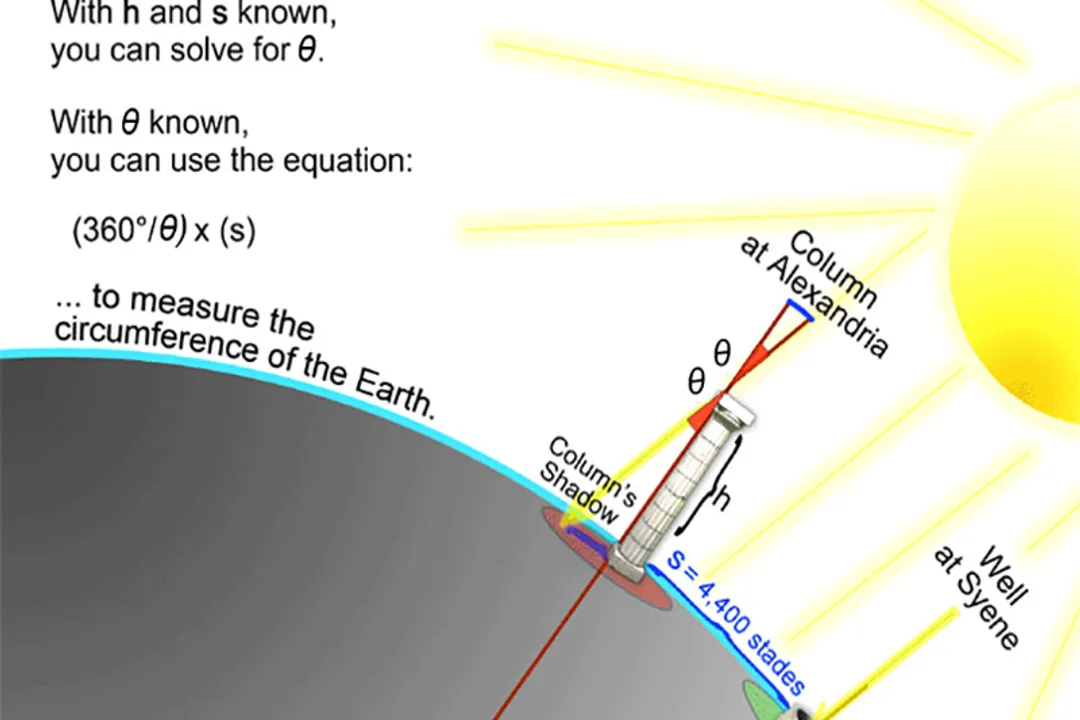
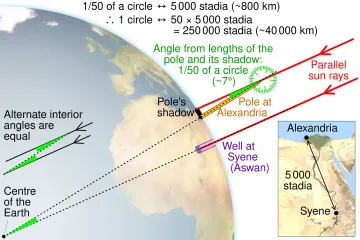
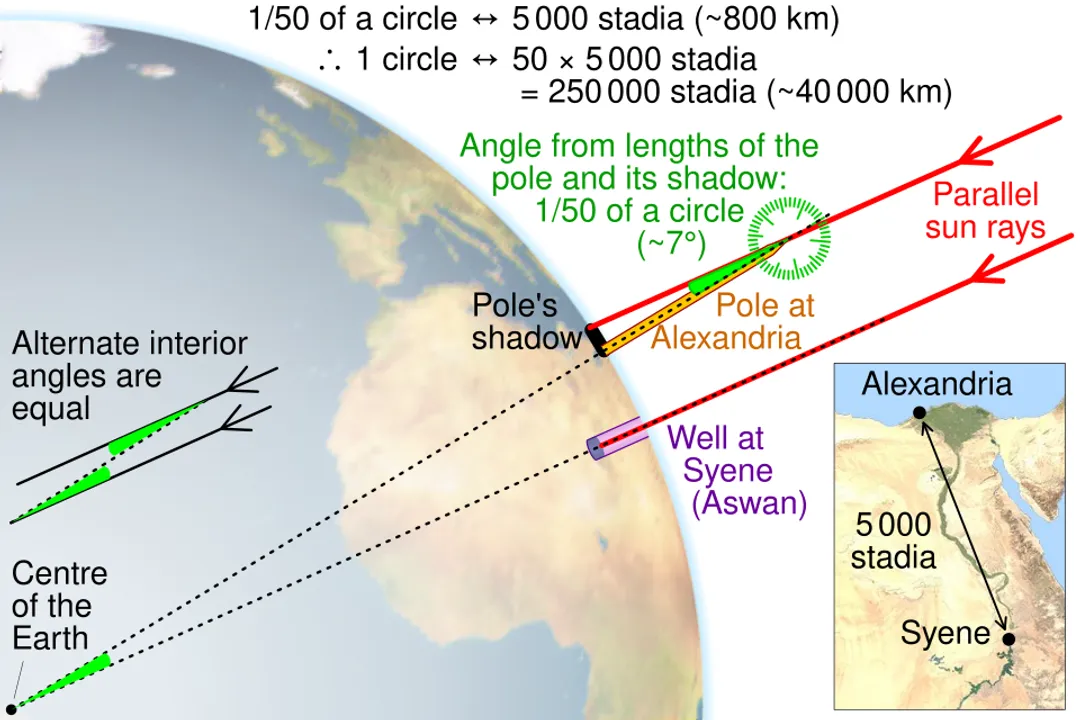
The very first, remarkably accurate attempts to measure the Earth's circumference relied on nothing more than the Sun's angle and the distance between two points. ^[7] The story often centers on the Greek scholar Eratosthenes around $240$ BCE. ^[6] He observed that in the city of Syene (modern Aswan), the Sun at noon on the summer solstice shone directly to the bottom of a deep well, meaning the Sun was directly overhead, casting no shadow. ^[7] At the same time in Alexandria, which he knew was due north of Syene, a vertical stick did cast a shadow. ^[6]

Eratosthenes reasoned that if the Sun's rays are considered parallel—a safe assumption given the Sun's immense distance—the angle of the shadow in Alexandria was equal to the angular separation between the two cities on the Earth's surface. ^[6] He measured this angle to be about $7.2$ degrees, which is $1/50$th of a full circle ($360^\circ / 7.2^\circ = 50$). ^[1][6] The final step required knowing the physical distance between Syene and Alexandria. While historical details vary on the exact method he used to measure this distance (perhaps by hiring professional pacers or using camel caravans), the accepted distance was about $5,000$ stadia. ^[7] Multiplying this distance by fifty gave him the Earth's circumference: approximately $250,000$ stadia. ^[6] Depending on how long a stadion was, this calculation was astonishingly close to the modern figure of about $40,075$ kilometers around the equator. ^[1] This effort established a foundational principle: measuring large-scale terrestrial dimensions relies on angular measurement over a known baseline. ^[3]

# Defining Shape

Even after establishing the circumference, scientists had to grapple with the fact that the Earth wasn't perfectly round. The concept that our planet is an oblate spheroid—flattened at the poles and bulging at the equator—was theorized based on physics related to centrifugal force from rotation. ^[3][8] This understanding mandated a move beyond simple circumference measurements to comprehensive geodesy—the science of measuring and understanding the Earth's geometric shape, orientation in space, and gravity field. ^[3]

To accurately map the planet or launch satellites, a standardized reference shape is needed. This is where the concept of a geodetic datum becomes essential. ^[3] A datum is essentially a mathematical model defining the origin and orientation of the coordinate system used for measurements on the Earth's surface. ^[3] Early datums often relied on a single, painstakingly surveyed baseline and a calculated meridian arc length to define the ellipsoid's parameters, such as its polar and equatorial radii. ^[3]

If we consider the equatorial radius to be $R_e$ and the polar radius to be $R_p$, the difference ($R_e - R_p$) quantifies the polar flattening. ^[3] For instance, the WGS 84 (World Geodetic System 1984) datum, which is the standard used by GPS, defines a specific set of parameters that approximate the Earth's true shape based on global measurements. ^[3] An interesting consequence of this shape is that the gravitational pull varies slightly across the surface, being marginally weaker at the equator due to the greater distance from the center of mass and the rotational effect. ^[8]

This distinction between a theoretical geometric figure (the reference ellipsoid) and the actual, irregular physical surface (the geoid, which corresponds to mean sea level) is vital for high-precision work. ^[3] Imagine plotting a pipeline or constructing a very long bridge; the engineering specifications must account for whether they are referencing the smooth, mathematically defined ellipsoid or the true, lumpy gravitational surface of the geoid. ^[3]

How do scientists measure the size of the Earth?

# Modern Surveying

As technology advanced, direct measurement moved from pacing distances to using precise triangulation and sophisticated instruments. Methods evolved to use larger arcs, such as measuring the arc length of a meridian between two latitudes with high accuracy. ^[6] Early geodesists established baselines, measured angles using instruments like the theodolite, and then calculated the rest of the survey network using trigonometry. ^[6] This technique provided a more precise map of local curvature.

One technique involves using specialized leveling instruments, often mounted on stable platforms or tripods, to determine the relative height differences between points. ^[3] While leveling primarily measures vertical change relative to a local surface, when combined with astronomical observations (like latitude and longitude fixes), it helps constrain the shape of the reference ellipsoid being used for that region. ^[3]

The shift from purely terrestrial methods to space-based geodesy dramatically increased accuracy and coverage. ^[5] While early measurements were limited by visibility, ground obstructions, and the difficulty of measuring long distances on curved terrain, modern science employs methods that essentially bypass the surface entirely.

# Satellite Geodesy

The most significant leap in measuring Earth's dimensions came with the advent of space technology. ^[5] Satellites offer an unobstructed view and the capability to measure vast distances and gravitational effects with unprecedented precision. ^[5]

# Laser Ranging

One key modern technique is Satellite Laser Ranging (SLR). ^[5] This involves powerful ground stations firing ultra-short laser pulses at retroreflectors placed on orbiting satellites. ^[5] The station precisely measures the time it takes for the light pulse to travel to the satellite and return. ^[5] Since the speed of light is known to an extremely high degree of accuracy, the distance to the satellite can be calculated to within a few millimeters. ^[5] By tracking satellites over time from multiple stations across the globe, scientists can refine the Earth's center of mass, measure crustal motion, and highly accurately determine the dimensions of the reference ellipsoid. ^[3][5]

# Global Navigation Systems

The Global Positioning System (GPS), along with similar systems like GLONASS and Galileo, represents the culmination of these efforts for everyday use. ^[5] GPS receivers determine their location by measuring the time difference in signals received from at least four orbiting satellites. ^[5] This process, known as trilateration, gives users their three-dimensional coordinates ($x, y, z$) relative to the WGS 84 reference frame. ^[3][5] While GPS is often thought of for navigation, its underlying precision is a direct measure of our knowledge of the Earth's size and the relative positions of ground stations that define the datum itself. ^[3]

It’s a fascinating feedback loop: we use GPS measurements to refine the mathematical model of the Earth (the datum), and we use the refined model to improve the accuracy of GPS signals. ^[3] This continuous refinement means that our understanding of the distance between, say, a fixed monument in Paris and one in Tokyo can be known to the centimeter level, helping map tectonic plate movement over time. ^[3]

# Very Long Baseline Interferometry (VLBI)

Another highly precise method used in geodesy is Very Long Baseline Interferometry (VLBI). ^[5] This technique involves simultaneously observing distant celestial radio sources (quasars) using multiple radio telescopes separated by thousands of kilometers. ^[5] By precisely comparing the arrival times of the radio signals at these different dishes, scientists can determine the distance between the telescopes with centimeter-level accuracy. ^[5] VLBI is crucial because it ties the terrestrial coordinate system directly to a fixed, extra-terrestrial reference frame, which helps measure minute shifts in the Earth's rotation and the orientation of the crust. ^[5]

How do scientists know how big the Earth is?

# Measuring Different Earth Properties

It is important to note the difference between measuring the Earth's size and measuring its age, as the techniques and timescales involved are entirely distinct, yet both contribute to our scientific understanding of the planet. ^[4] Determining the age of the Earth—estimated to be about $4.54$ billion years old—involves analyzing radioactive isotopes in ancient rocks and meteorites, a field known as radiometric dating. ^[4] This tells us when the Earth formed, whereas geodesy tells us how big it is now. ^[4]

Similarly, measuring the Earth's interior density or its magnetic field requires entirely different physics, often relying on seismology (analyzing earthquake waves) or magnetometers, rather than line-of-sight or orbital measurements. ^[8] For example, the Earth’s average density is about $5.51$ grams per cubic centimeter, which is much greater than the density of surface rock, indicating a dense core. ^[8]

# Current Dimensions

Thanks to the convergence of space geodesy, advanced modeling, and centuries of terrestrial surveying, we have highly accurate figures for the Earth's dimensions. ^[1][8] While the specific values can shift slightly depending on the chosen geodetic datum (as they are models of an imperfect shape), the general consensus based on systems like WGS 84 is clear. ^[3]

The Earth is not uniform, but we often quote averages for practical use. The equatorial diameter is approximately $12,756$ kilometers, whereas the polar diameter is slightly less, around $12,714$ kilometers. ^[1][9] This small difference of about $42$ kilometers is what defines its "oblate" nature. ^[3]

If you were to measure the circumference along the equator, the distance is about $40,075$ kilometers. ^[1] Measuring around the poles, the polar circumference is slightly shorter, at approximately $40,008$ kilometers. ^[1]

Consider a hypothetical scenario: If you were a local surveyor in a region with complex topography and were tasked with ensuring a new highway grade perfectly matched the long-term mean sea level (the geoid) over a $100$-kilometer stretch, you couldn't rely solely on satellite coordinates from WGS 84. You would need a detailed, localized gravity survey to map the geoid undulations in that area. ^[3] The global models account for the main bulge, but local topographical features, large underground mineral deposits, or massive ice sheets cause slight local variations in gravity that pull the actual sea level away from the smooth reference ellipsoid—a subtlety that demonstrates the need for both the grand, global space-based measurements and the fine-tuned local ground checks. ^[3]

This continuous measurement process, whether through laser ranging or the foundational geometry pioneered by Eratosthenes, shows science as an iterative process. Each generation builds upon the angular measurements and known distances of the last, refining the picture of our planet from a simple marble to a dynamic, slightly squashed, rotating sphere whose precise shape governs everything from GPS accuracy to ocean currents. ^[5]