How do scientists measure the size of the Earth?

The sheer scale of the Earth often makes us take its size for granted. We rely on maps and GPS coordinates daily, yet pondering how people first figured out the circumference of our planet—a globe nearly 25,000 miles around—reveals a magnificent history of observation and applied mathematics. Before satellites could beam back images, thinkers had to rely on sticks, shadows, and simple geometry to quantify the vastness beneath their feet. ^[7][9]

# Ancient Shadows

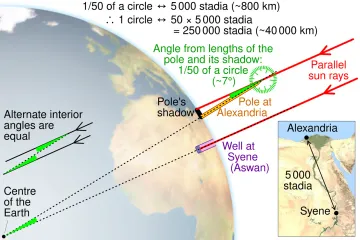
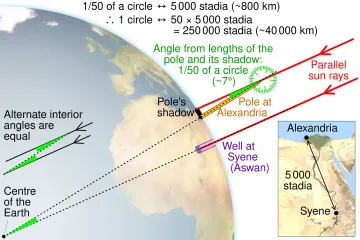
The earliest, and arguably most elegant, measurement of the Earth’s circumference is credited to the ancient Greek mathematician and geographer Eratosthenes around 240 BC. ^[7] His method was brilliant in its simplicity, relying on the assumption that the Earth is spherical and that the sun's rays arrive parallel to the Earth's surface. ^[5][7]

Eratosthenes knew that in the city of Syene (modern Aswan, Egypt), the sun shone directly down a deep well at noon on the summer solstice, meaning the sun was precisely overhead—no shadows were cast. ^[7][9] He also knew that at the same moment in Alexandria, located due north, a vertical stick did cast a shadow. ^[7]

The core of his experiment was to measure the angle of that shadow in Alexandria. By measuring the shadow's length and comparing it to the height of the stick, he could calculate the angle of divergence from the vertical sun, which, thanks to parallel sun rays, directly corresponded to the angular separation between the two cities on the Earth's surface. ^[5][7][9] He found this angle to be about 7.2 degrees. ^[7]

# Distance Calculation

To complete the calculation, Eratosthenes needed one more critical piece of information: the distance between Syene and Alexandria. This distance was estimated to be about 5,000 stadia, possibly measured by professional pacers called bematists. ^[7][5]

Since 7.2 degrees represents a fraction of the full circle (360 degrees), the relationship is straightforward: if 7.2 degrees of arc equals 5,000 stadia, then the full 360 degrees must equal $360 / 7.2$ times that distance. ^[7]

$$\frac{360^\circ}{7.2^\circ} = 50$$

Multiplying $50$ by $5,000$ stadia gives a circumference estimate of 250,000 stadia. ^[7] The exact modern equivalent depends on which historical measurement of the stadion Eratosthenes used, but the result was remarkably close to the actual value. If we use the Attic stadion, his estimate translates to a circumference of about 39,690 kilometers, which is only about 1% off the modern accepted polar circumference of approximately 40,008 km. ^[7] This feat, accomplished with basic geometry, stands as a testament to early scientific reasoning. ^[5]

# Beyond Spheres

While Eratosthenes assumed a perfect sphere, later investigations revealed a more nuanced picture of our planet's shape. Scientists realized that the Earth is not a perfect ball; it is an oblate spheroid. ^[6] This means it bulges slightly at the equator and is flattened at the poles due to the centrifugal force generated by the planet's rotation. ^[6][2]

The difference in these measurements is subtle but scientifically significant. For general purposes, the equatorial radius is often cited as approximately $6,378$ kilometers, while the polar radius is slightly smaller, around $6,357$ kilometers. ^[6] Understanding this slight deviation is crucial for high-precision work, especially in fields like geodesy, which is the science of accurately measuring and understanding the Earth's geometric shape, orientation in space, and gravity field. ^[2] These measurements form the basis for coordinate systems and datums, which are the reference frameworks for all mapping activities. ^[2]

How do scientists measure the Earth?

# Modern Tools

Today, measuring the Earth is less about shadows and more about signals traveling vast distances, often involving space-based technology. Scientists now employ several advanced techniques to determine the Earth's size, shape, and changes in that shape with millimeter precision. ^[4]

# Satellite Geodesy

One of the primary methods involves satellite geodesy, which relies on tracking satellites orbiting the Earth. ^[4] Techniques like the Global Positioning System (GPS) and its international counterparts are foundational. GPS receivers on the ground calculate their position by timing signals received from multiple satellites. ^[4] By knowing the precise orbits of the satellites—determined through tracking stations on Earth—scientists can accurately map the ground stations and, by extension, the shape of the Earth model they are based upon. ^[4]

# Laser Ranging

For an even higher degree of precision, scientists turn to Satellite Laser Ranging (SLR) and Lunar Laser Ranging (LLR). ^[4][3] In SLR, ground stations fire extremely short, powerful laser pulses at specialized satellites equipped with retroreflectors. ^[4] The time it takes for the laser light to travel to the satellite and return, measured with incredible accuracy, allows scientists to calculate the distance to the satellite with high precision. ^[4] This data helps refine the Earth's center of mass and its precise shape over time. ^[3] Similarly, LLR involves bouncing lasers off reflectors left on the Moon by Apollo astronauts to measure the Earth-Moon distance, which also helps refine geophysical models. ^[3]

# VLBI

Another powerful technique is Very Long Baseline Interferometry (VLBI). ^[3] This method uses signals from distant cosmic radio sources, known as quasars, observed simultaneously by widely separated radio telescopes on Earth. ^[3] By comparing the arrival times of the radio waves at different observatories, scientists can determine the exact distance between those observatories and track minute tectonic movements and Earth's rotation variations with extreme accuracy. ^[3]

# Measuring Curvature Locally

While the methods above focus on the global scale, the principle of curvature can be observed—and even measured—on a much smaller, local scale, which offers a practical way to relate ancient concepts to modern experience.

Imagine you are standing on a very long, straight stretch of coast or a railway track extending toward the horizon. If you could measure the height of a distant object, like a lighthouse or a radio tower, as you move away from it, you would find that the base of the object disappears from view before the top does. ^[2] This is direct visual evidence of the Earth's curvature hiding the lower parts of the object. The distance to the geometric horizon, where the line of sight just grazes the surface, can be calculated if the observer's height is known. ^[2]

For instance, if you are standing at an observer height ($h$) of about $1.7$ meters (roughly $5.5$ feet), the geometric distance to the horizon ($d$) can be approximated using a simplified formula derived from the Earth's radius ($R \approx 6371$ km):

$$d \approx \sqrt{2Rh}$$

Plugging in the values gives a horizon distance of about $4.7$ kilometers. ^[2] This calculation shows that even over a few kilometers, the planet's curve is already obstructing your view of the ground, illustrating why surveyors and engineers must account for this curvature in large-scale construction projects, such as long bridges or railway lines. ^[2]

How do scientists know how big the Earth is?

# Pendulum Physics

An unexpected, albeit less precise, method involving the physics of motion relates to the size of the Earth: the pendulum. ^[1] The time it takes for a pendulum to complete one swing, its period, is affected by gravity. ^[1] Since gravity slightly changes depending on your distance from the Earth's center of mass, the period of an identical pendulum will vary slightly depending on whether it is swinging at the North Pole or on the equator. ^[1] This variation in the acceleration due to gravity ($g$) allows physicists to map out slight changes in the planet's radius across the surface, corroborating the oblate spheroid model derived from space-based observations. ^[1][2]

The consistency across these wildly different methods—ancient shadow tracking, high-speed lasers timed to the nanosecond, and the subtle swing of a weight on a string—is what builds trust in our scientific understanding of our home planet. Every technique, from Eratosthenes' stick to modern VLBI, attempts to solve the same fundamental problem: defining the dimensions of the world we inhabit. ^[4]