How did we determine the size of the Earth?

The realization that our world was a massive sphere floating in space did not begin with space telescopes or GPS satellites. Long before any human ever left the ground, thinkers in the ancient world had already worked out the rough dimensions of the planet using nothing more than shadows, geometry, and careful observation. It’s a testament to human curiosity that such a fundamental measurement could be pinned down with surprising accuracy over two millennia ago, establishing a foundational piece of geographical knowledge.

# Spherical Thinking

For many ancient cultures, the idea of a flat Earth was the default assumption. However, by the time of classical Greece, many scholars had moved past that simple view. Evidence supporting a spherical Earth was accumulating, often derived from astronomical observations and the way ships disappeared over the horizon. The ancient Greeks, with their advanced understanding of mathematics and geometry, were perfectly poised to transition from knowing the Earth was round to measuring how big that roundness actually was.

The Greeks understood that the stars appeared to shift positions as one traveled north or south, which is a direct consequence of viewing the sky from different points on a curved surface. This knowledge laid the groundwork for the first serious attempt to quantify the globe's size.

# Eratosthenes’ Trick

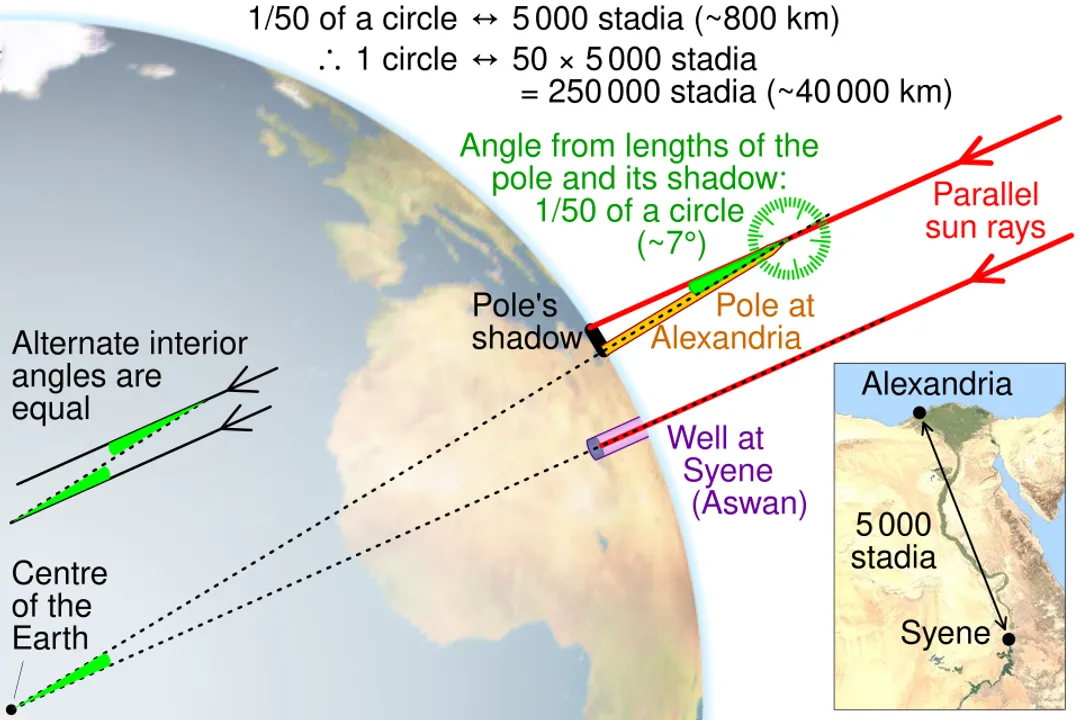
The most famous and scientifically sound early measurement comes from Eratosthenes of Cyrene, a brilliant scholar who lived in Alexandria, Egypt, around the third century BCE. His approach was elegantly simple, relying on a single, precise observation that he was able to compare with a known distance.

Eratosthenes knew a curious fact about the city of Syene (modern Aswan), located significantly south of his home in Alexandria. He had heard or observed that at noon on the summer solstice—the longest day of the year—the sun shone directly down into a deep, vertical well in Syene, meaning the sun was perfectly at the zenith, casting no shadow whatsoever.

The critical comparison came when he measured the shadow cast by a vertical stick, known as a gnomon, in Alexandria at that exact same time and date. Unlike Syene, Alexandria did cast a shadow. This difference proved that Alexandria and Syene were not in the same line relative to the sun, meaning the Earth's surface curved between the two cities.

# Geometry and Angles

Eratosthenes made two core assumptions, both of which were reasonable for his time but introduced the potential for error: first, that the Earth was a perfect sphere, and second, that the Sun was so far away that its incoming rays struck the Earth essentially parallel to one another.

If the sun's rays are parallel, then the angle of the shadow cast in Alexandria ($7.2^\circ$) must be equal to the angle subtended by the arc connecting Syene and Alexandria at the center of the Earth. This is a classic application of geometry using alternate interior angles.

He determined this angle to be about $7.2$ degrees. A full circle is $360$ degrees, so $7.2^\circ$ represents a fraction of the total circumference:

$$\frac{360^\circ}{7.2^\circ} = 50$$

This meant that the distance between Syene and Alexandria accounted for exactly $1/50$th of the Earth's total circumference.

# Measuring the Ground Distance

The final piece of the puzzle was determining the distance between the two cities. This was done not by measuring with a ruler, but by hiring professional surveyors or "pacers" called bematists. These individuals walked the distance, meticulously counting their steps, which was a standardized measurement of the time. The distance measured or estimated was about $5,000$ stadia.

Multiplying the segment distance by the ratio yielded his result:

$$5,000 \text{ stadia} \times 50 = 250,000 \text{ stadia}$$

Eratosthenes refined this slightly to $252,000$ stadia, possibly to make the final result divisible by 60, a number important in ancient mathematics.

It is fascinating to consider the precision required in the field measurement alone. While the geometrical concept is flawless, the accuracy of the final circumference hinges entirely on two variables: the angular measurement ($7.2^\circ$) and the distance traveled (5,000 stadia). An error of just a few hundred feet in the distance walked over nearly 500 miles could translate into a significant percentage error in the final circumference calculation. This highlights that in early science, the difficulty often lies not in the theory, but in the execution of precise measurement on an imperfect physical landscape.

How do scientists measure the size of the Earth?

# The Stadium Discrepancy

The brilliance of Eratosthenes’ work is undeniable, but converting his final answer into modern units remains a subject of scholarly debate because the exact length of the stadion varied geographically and temporally.

If we assume he used the common Egyptian stadion of about $157.5$ meters, his $252,000$ stadia converts to roughly $39,690$ kilometers (about $24,660$ miles). The modern accepted value for the Earth’s polar circumference is about $40,008$ kilometers (around $24,860$ miles). This places his calculation within about $1%$ of the actual figure, a remarkable achievement for the third century BCE.

Other interpretations of the stadion unit suggest his result was $15%$ too large compared to the modern equatorial circumference, but even this range demonstrates an incredible level of scientific success given the tools available. The key takeaway isn't the exact final number, but the demonstration that the Earth's size was knowable through observation and deduction rather than divine pronouncement or pure guesswork.

# Measuring the Meridian

The technique used by Eratosthenes determined the length of one meridian arc—the distance corresponding to $7.2^\circ$ of latitude change. Later scientists, including the great astronomer Ptolemy, also made estimates, though his value was slightly smaller than Eratosthenes'.

A subsequent major effort to accurately map the meridian arc came much later, driven by the needs of navigation and cartography. By the 17th and 18th centuries, mathematicians and explorers realized that to create accurate maps, they needed to know if the Earth was a perfect sphere or an oblate spheroid—a sphere flattened slightly at the poles due to rotation.

This debate led to the famous French Academy of Sciences expeditions in the 1730s. One team, led by Pierre Louis Maupertuis, measured a degree of latitude near the Arctic Circle (in modern-day Finland/Lapland). Another team, led by Charles Marie de La Condamine, measured the same degree near the equator (in modern-day Peru).

The results confirmed the theoretical prediction: the length of one degree of latitude was longer near the poles than near the equator. This proved that the Earth bulges at the equator, giving it its slightly flattened, oblate shape. This confirmed the necessity of defining a datum, which is a reference system used in geodesy to tie measurements together, accounting for the planet's actual shape.

How does the size of a star determine what elements are created?

# Modern Precision

Today, determining the size and shape of the Earth—the science known as geodesy—has moved from pacing and shadow sticks to incredibly precise satellite technology.

Modern measurements rely on several advanced techniques:

1. Satellite Laser Ranging (SLR): Scientists bounce laser beams off retroreflectors placed on satellites and time the round trip. This yields extremely accurate distances between ground stations, helping define the Earth's center of mass and its shape.
2. Very Long Baseline Interferometry (VLBI): This technique observes radio waves from distant quasars using widely separated radio telescopes, which provides precise measurements of the relative positions of the telescopes.
3. Global Positioning System (GPS): While best known for navigation, the GPS network is fundamentally a geodesy tool, constantly refining the coordinates of points on the Earth's surface based on satellite time signals.

These methods allow us to define the Earth's size not just as a single number, but as a model that accounts for its irregular gravity field and topographical variations. The Earth is not truly a perfect ellipsoid; it has small bumps and dips caused by mass concentrations beneath the surface. The reference surface that best approximates global mean sea level, taking these irregularities into account, is called the geoid.

The modern calculated equatorial circumference is approximately $40,075$ kilometers, while the polar circumference is about $40,008$ kilometers. The difference, though small relative to the total size, confirms the fundamental shape deduced centuries after Eratosthenes by the Lapland and Peruvian expeditions.

The arc measurement concept lives on, even if the tools have changed. Think of modern GPS—every time your phone calculates a position, it is using measurements derived from signals traveling across the planet, effectively performing a hyper-accurate, three-dimensional version of Eratosthenes’ original calculation over an arc defined by orbiting satellites rather than just two sticks on the ground. The initial genius lay in recognizing that a local measurement of shadow could reveal a global constant.