Why does a high mass star have a short life cycle?

The first question anyone asks when learning about stellar evolution is often why the biggest objects in the sky have the shortest lives. It seems like a cosmic paradox: a star with substantially more raw material—more mass—should logically burn that fuel for a longer time. Yet, the observational evidence and stellar models overwhelmingly show the opposite is true. The most massive stars, often appearing brilliant blue, blaze briefly, measured in millions of years, while the smallest, dimmest stars, like the omnipresent red dwarfs, can theoretically continue shining for trillions of years, outliving the current age of the universe itself. This fundamental difference in stellar destiny is dictated almost entirely by one factor: mass.

# The Cosmic Budget

A star spends the vast majority of its existence in the stable phase known as the main sequence, diligently fusing hydrogen into helium in its core. This phase is only possible because of a precarious, self-regulating balance known as hydrostatic equilibrium. On one side of the scale is gravity, the crushing inward force generated by the star’s enormous mass, trying to collapse the entire structure. On the other side is the outward radiation pressure created by the thermonuclear reactions happening in the core. As long as the energy production rate precisely matches what is needed to counteract gravity, the star remains stable.

The immediate consequence of having a greater mass is a much stronger gravitational pull requiring a proportionally greater counter-pressure to maintain this equilibrium. To generate this necessary outward pressure, the core of a massive star must be far hotter and denser than that of a low-mass star. This heightened core temperature is the direct catalyst that accelerates the rate of nuclear fusion.

Think of it like a massive, self-regulated furnace. A small increase in the furnace's operating temperature (core temperature) leads to an exponential increase in the rate at which it consumes its fuel (nuclear fusion rate). For a high-mass star, this effect is dramatic. The energy production process, whether the proton-proton chain dominant in Sun-like stars, or the CNO cycle in hotter, more massive stars, runs much harder and faster.

# The Mass-Luminosity Exponent

This relationship between mass and energy output—or luminosity—is not linear; it is steeply skewed. For main-sequence stars in the range of $0.1$ to $50$ solar masses ($M_\odot$), the luminosity ($L$) scales with mass ($M$) to a power that is frequently approximated as the $3.5$ power: $L \propto M^{3.5}$.

To grasp the impact of this non-linear relationship, consider a star that is ten times more massive than our Sun ($10 M_\odot$). It possesses $10$ times the amount of fuel. However, because its luminosity scales roughly as $M^{3.5}$, it radiates energy at a rate of $10^{3.5}$, which is approximately $3,162$ times the Sun's luminosity.

The star's primary lifespan ($\tau_{\text{MS}}$) on the main sequence is determined by how much fuel it has versus how fast it burns it: $\tau_{\text{MS}} \propto M/L$. Substituting the proportionality for luminosity, the lifetime scales inversely with mass raised to the power of $2.5$: $\tau_{\text{MS}} \propto M/M^{3.5} \propto M^{-2.5}$.

If we compare our $10 M_\odot$ star to the Sun (which has a main-sequence life of about $10$ billion years):
$$\tau_{\text{MS}} \approx 10^{10} \text{ years} \times \left(\frac{M}{M_\odot}\right)^{-2.5}$$
For the $10 M_\odot$ star, this calculation suggests a main-sequence lifetime of only about $31.6$ million years.

# Fuel Conservation vs. Consumption Rate

It is easy to fall into the trap of thinking that having $10$ times the fuel should easily compensate for burning it $3,000$ times faster. However, the physics of stellar cores dictates that the rate of burning is far more sensitive to mass than the available supply of fuel. A star twice as massive as the Sun burns its hydrogen fuel $16$ times faster. Even though it has twice the initial fuel, it exhausts it $8$ times faster ($2 / 16 = 1/8$).

A helpful analogy is to picture two households with very different spending habits. The low-mass star is like an extremely frugal individual who lives on the bare minimum; they have a small pantry, but they ration their food so effectively that they can survive for centuries. The high-mass star, by contrast, is like a lottery winner with an enormous mansion stocked with provisions, but they host massive, non-stop parties every night, spending their wealth at an astronomical rate. Despite having more initial resources, the massive spender will run out of funds—or in this case, available core hydrogen—far sooner than the frugal counterpart.

# Beyond Hydrogen Burning

The disparity in lifespan is compounded once the star exhausts the hydrogen in its core and begins fusing heavier elements. In low-mass stars like the Sun, once core hydrogen is gone, they ignite helium fusion into carbon, a process that releases about one-tenth the energy per unit mass compared to hydrogen fusion. This transition causes the star to swell into a red giant and spend a relatively brief period (about $130$ million years for the Sun) before reaching its end as a white dwarf.

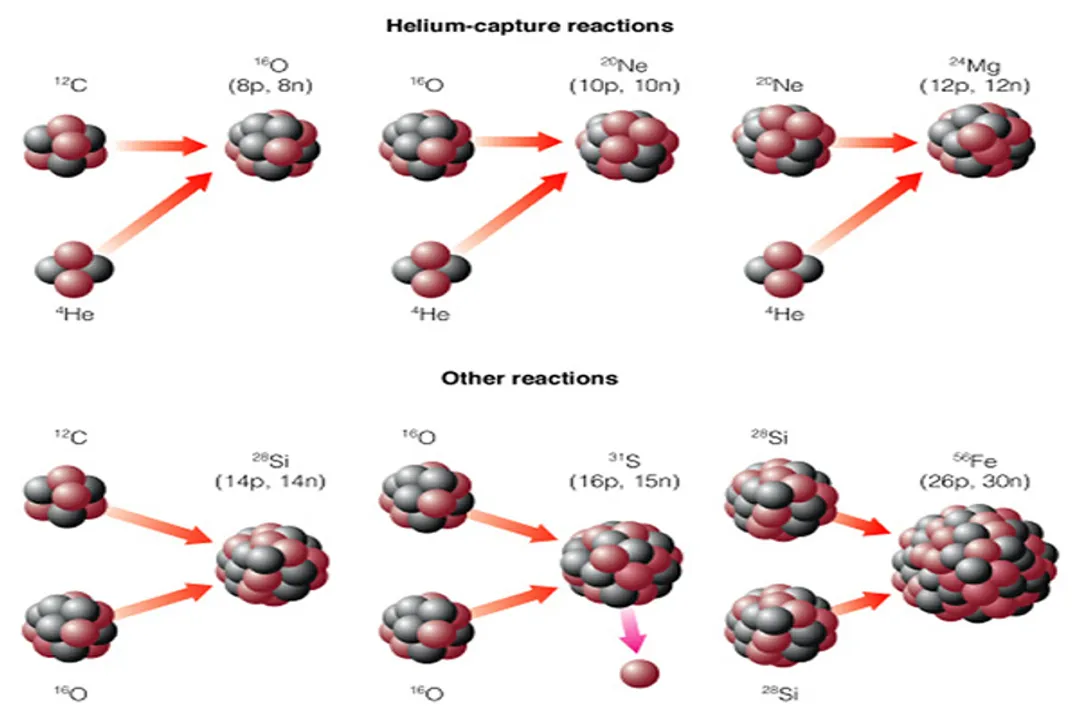
High-mass stars, those generally greater than $8$ times the Sun's mass, proceed much further, thanks to their overwhelming gravitational pressure and core temperatures. After hydrogen fusion, they can successfully fuse helium into carbon, then carbon into neon, and continue through a cascade of increasingly heavier elements, forming an "onion-like" structure of shells.

# Rapid Fire Fusion

The critical factor here is that each successive burning stage generates less net energy than the one before it, yet it must still support the immense weight of the star’s outer layers. As the energy output per reaction decreases, the star's core must contract, heat up, and increase the reaction rate again to maintain equilibrium or initiate the next reaction.

This results in evolutionary stages that shorten dramatically in duration. Using the example of a star roughly $25$ times the mass of the Sun:

• Hydrogen burning might last about $7$ million years.
• Helium burning might last $700,000$ years.
• Carbon burning might last only $600$ years.
• Neon burning might last just $1$ year.
• Oxygen burning lasts about $6$ months.
• Silicon burning is over in about one day.

The progression from one fuel to the next is not a gradual slowdown but a headlong rush toward the final, inevitable energy sink.

# The Iron Wall

This desperate, rapid-fire fusion cycle comes to an absolute halt when the core begins to form iron ($\text{Fe}$). Iron represents the end of the line for energy-releasing nuclear fusion in stars because, unlike lighter elements, fusing iron requires an input of energy rather than releasing it.

When the core becomes inert iron, the star loses its primary energy source almost instantaneously. The outward pressure supporting the star vanishes, and gravity wins the final, overwhelming victory. This is not a slow fade; the core collapses catastrophically in less than a second. The temperature in the core can surge past $100$ billion degrees.

How do stars produce elements throughout their life cycle?

# Death's Spectacular Finale

The collapse of the iron core is so violent that it triggers a rebound shockwave, tearing the rest of the star apart in what we observe as a supernova explosion. This event is so energetic that it momentarily outshines entire galaxies and is responsible for forging all elements heavier than iron in the universe.

The end state depends on the mass of the remnant core after the explosion:

• If the original star was massive (e.g., $8$ to $20$ solar masses), the collapse might be halted by neutron degeneracy pressure, forming an ultra-dense neutron star—an object only about $15$ kilometers in diameter, yet holding up to three times the mass of the Sun.
• If the original star was exceedingly massive (over approximately $20$ solar masses), gravity overcomes even neutron degeneracy pressure. The core collapses indefinitely, creating a black hole from which nothing, not even light, can escape.

In summary, the reason high-mass stars live fast and die young is because their superior mass translates into an exponentially higher core temperature and fusion rate. While they possess a larger initial tank of fuel, their colossal rate of consumption, enforced by the constant struggle against greater gravity, ensures they burn through their supply in a stellar blink of an eye compared to their smaller, more temperate cosmic neighbors. The very structure that allows them to shine so brilliantly is the mechanism that guarantees their swift demise.