What limits the efficiency of heat engines?

The quest to convert heat into useful work has driven technological advancement for centuries, yet every machine designed for this task—from the steam engine to the modern gas turbine—operates with inherent limitations on how much energy it can actually transform. These limitations are not merely a matter of poor engineering or cheap materials; they are fundamentally dictated by the laws of physics. Understanding what restricts the efficiency of a heat engine means diving into the core principles of thermodynamics, specifically the relationship between temperature differences and the impossibility of perfect energy conversion.^[1][4]

# Efficiency Definition

At its simplest, the thermal efficiency, often denoted by the Greek letter eta ($\eta$), of a heat engine measures how effectively it converts the heat energy it absorbs into mechanical work. It is calculated as the ratio of the net work output ($W$) to the total heat input ($Q_H$) taken from the high-temperature source: $\eta = W / Q_H$. ^[1][2] Since energy cannot be created or destroyed (First Law of Thermodynamics), the heat energy that is not converted into work ($Q_C$) must be rejected to a lower-temperature sink. This rejected heat must always be greater than zero for any real process, meaning that $\eta$ must always be less than one, or 100%. ^[1][4] A 100% efficient engine would require all heat input to be perfectly converted to work, with no residual heat rejected to the environment, a scenario prohibited by the laws governing energy transfer.^[4][8]

# Carnot Limit

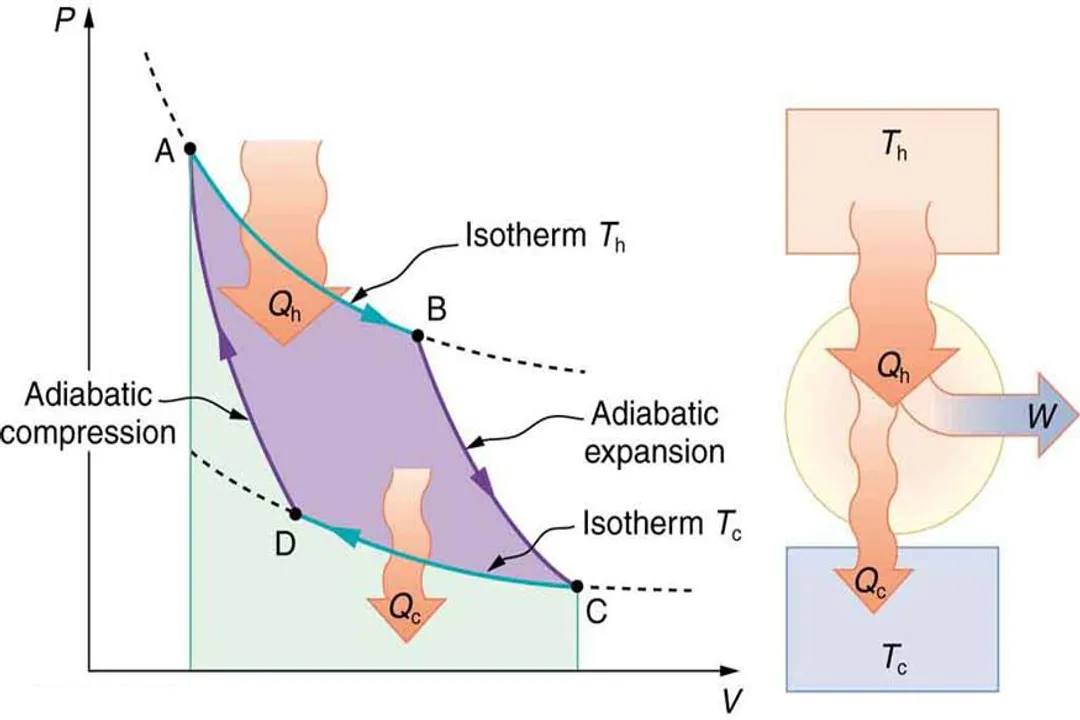
The absolute theoretical ceiling for any heat engine operating between two specified temperatures is set by the Carnot limit, derived from the reversible Carnot cycle. ^[3][4] This theoretical construct imagines an idealized engine that experiences no dissipative losses, such as friction, and whose heat transfers occur infinitesimally slowly across a system in near-equilibrium, meaning the temperature difference driving the heat flow is vanishingly small. ^[4] The efficiency of such a perfect, hypothetical engine is determined exclusively by the absolute temperatures of the high-temperature source ($T_H$) and the low-temperature sink ($T_C$):

$$\eta_{\text{Carnot}} = 1 - \frac{T_C}{T_H}$$

Crucially, these temperatures must be expressed in an absolute scale, such as Kelvin. ^[3][4] This formula immediately reveals the primary theoretical constraint: efficiency is a function only of the temperature ratio, not the working fluid, the design, or the specific details of the cycle (like the Brayton or Rankine cycle used in real engines). ^[4][6]

# Temperature Dependence

The mathematical expression makes it clear that to maximize efficiency, an engineer must maximize $T_H$ and minimize $T_C$. ^[4][5] The cold reservoir ($T_C$) is typically environmental—the ambient air or a body of cooling water—and is largely fixed by geography and climate. Therefore, the practical battle for higher efficiency is often fought at the hot end. If $T_H$ were to equal $T_C$, the ratio $T_C/T_H$ would equal one, making the Carnot efficiency zero, meaning no work could be extracted. ^[1][4] This underscores the necessity of a temperature gradient; work extraction is fundamentally tied to the existence of a hot reservoir supplying energy and a cold reservoir receiving the waste heat. ^[8]

Imagine two power plants. Plant A operates with a maximum temperature of $900 \text{ K}$ and rejects heat at $300 \text{ K}$ (a common environmental temperature). Its theoretical maximum efficiency is $1 - 300/900 \approx 66.7\%$. Plant B, using more advanced materials, can sustain a temperature of $1200 \text{ K}$ while also rejecting at $300 \text{ K}$. Its Carnot efficiency jumps to $1 - 300/1200 = 75\%$. This is a significant jump, showing that even incremental increases in operating temperature yield substantial theoretical gains. ^[4]

What limits wind turbine efficiency?

# Second Law Implication

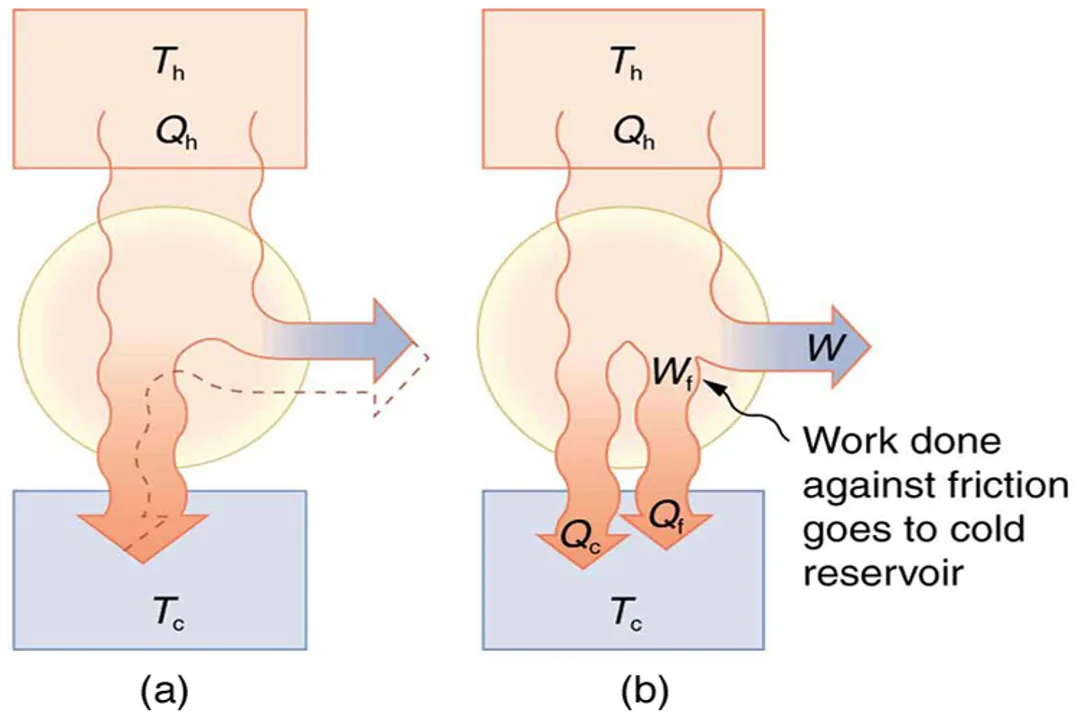
The Carnot limit is not an arbitrary benchmark; it is a direct manifestation of the Second Law of Thermodynamics. ^[4][8] The law can be restated in this context to say that no heat engine operating between two thermal reservoirs can be more efficient than a reversible engine operating between the same two reservoirs. ^[4][8] While the First Law deals with the quantity of energy, the Second Law deals with its quality or usefulness. Heat flowing from hot to cold is a process that increases the overall entropy of the universe, and work can only be extracted during this spontaneous flow. ^[8] Any attempt to achieve 100% efficiency would imply a process where entropy remains unchanged or decreases, violating the Second Law. ^[4]

# Practical Hurdles

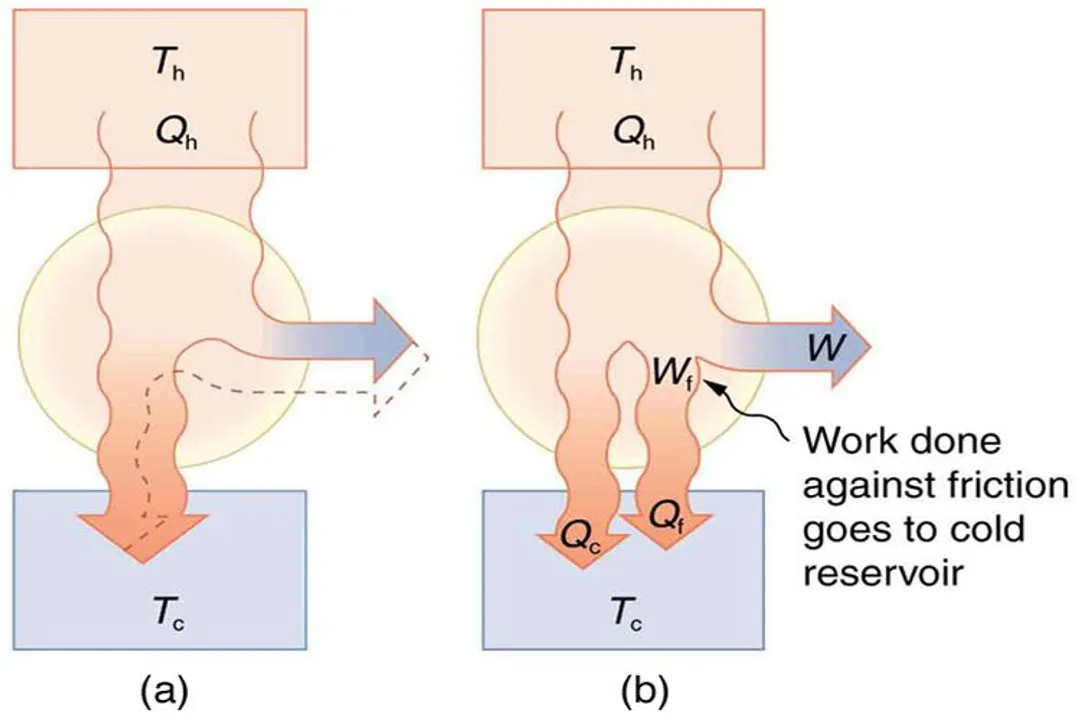
While the Carnot efficiency provides the ultimate theoretical boundary, real-world heat engines are always less efficient because they operate irreversibly. ^[2] The theoretical limit assumes a reversible process, but actual engineering systems involve unavoidable sources of inefficiency that increase entropy beyond what is required for the simple temperature differential. ^[7]

These practical limitations fall into several categories:

1. Finite Temperature Differences: In a real cycle, heat must be transferred from the fuel/combustion chamber to the working fluid (e.g., steam or air) and then from the working fluid to the cold sink. To achieve a useful rate of energy transfer, these heat exchanges must occur across a finite, non-zero temperature difference. For example, a steam boiler operates at $600 \text{ K}$ while the combustion gases might be $1500 \text{ K}$. This gap, where $T_{\text{gas}} > T_{\text{steam}}$, represents an inherent, irreversible loss of potential efficiency compared to the idealized Carnot process where the heat transfer occurs at a single, constant temperature. ^[2][7]
2. Friction and Viscous Effects: Mechanical friction between moving parts—pistons, bearings, turbines—converts kinetic energy directly into unusable heat, which must then be accounted for as part of the $Q_C$ rejection. ^[2] Air or fluid flowing through pipes, valves, and turbine blades experiences viscous drag, causing pressure drops and energy dissipation that are likewise lost to the system's potential work output. ^[7]
3. Incomplete Expansion or Compression: Real cycles often do not perfectly follow the isentropic (frictionless, adiabatic) paths assumed in ideal analyses. For example, a gas turbine's compression phase requires work input, and if that process is inefficient due to flow issues, more initial work is expended than necessary, reducing the net work output for the same heat input. ^[2]
4. Heat Loss: Engines lose heat to the surroundings through imperfect insulation, which means some of the input energy ($Q_H$) bypasses the work-producing parts of the engine entirely. ^[7]

A typical modern coal-fired power plant might have a practical efficiency of around 40-45%. If its operating temperatures dictate a Carnot limit of, say, 65%, the remaining $20-25%$ difference between the ideal and actual performance stems almost entirely from the irreversible processes described above. ^[2]

What limits human lifespan biologically?

# Engineering Trade-offs in Practice

The pursuit of efficiency forces engineers to operate right at the edge of material science capabilities. As the Carnot equation shows, the best path to higher efficiency is raising $T_H$. However, this pushes the materials in the turbine blades or boiler tubes to their limits. ^[4] Materials weaken, creep, and degrade at extremely high temperatures. Therefore, an engineering design is often a negotiation: maximizing $T_H$ to approach the thermodynamic limit while ensuring the structural integrity of the components over the required lifespan. ^[5]

This introduces a subtle, non-thermodynamic constraint. Consider a gas turbine. Increasing the firing temperature dramatically improves the Carnot-limited potential. However, if achieving that temperature requires coating blades with expensive, specialized thermal barrier coatings (TBCs) that have a limited lifespan or significantly increase the manufacturing cost of the engine, the economic efficiency might decrease. The best engineering solution often sits below the highest possible temperature, balancing the thermodynamic gain against material cost and durability. This means that while the limit is purely thermal, the achieved performance is constrained by the properties of matter itself, a subtle yet significant practical barrier beyond just the Second Law.

# The Limits of Temperature

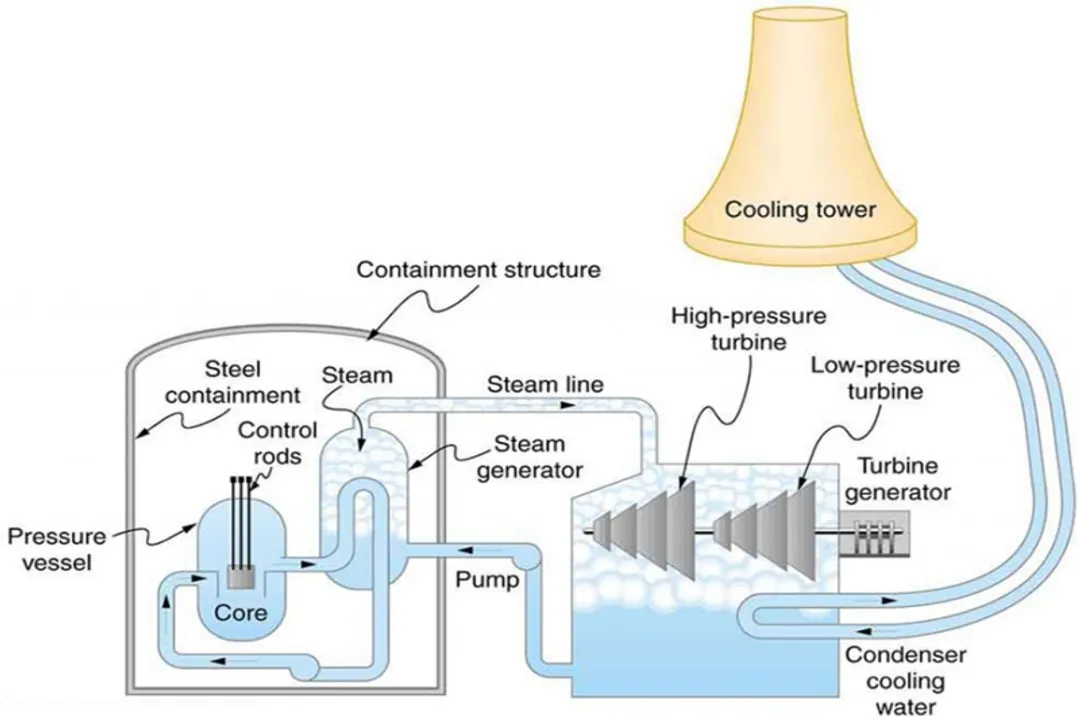
The need to raise $T_H$ is relentless, but it runs into physical boundaries. Even if we imagine a perfect, frictionless engine, we cannot exceed the temperature at which the materials of construction begin to fail, melt, or chemically react destructively with the working fluid. For instance, in a nuclear power plant, the heat source is nuclear fission, which can produce extremely high temperatures, but the steam generator and turbine materials limit the practical operating temperature to far below what the fuel itself could potentially generate. This creates a secondary, material-based limit that sits below the Carnot limit dictated by the external heat source and sink temperatures.

The cold sink temperature ($T_C$) also presents an interesting, often overlooked practical constraint. In areas with consistently hot climates, the available cooling water or air for condensation (in Rankine cycles) or heat rejection (in gas cycles) is already warmer than in cooler regions. This means that two identical engine designs, one in Norway and one in the Sahara, will have different potential Carnot efficiencies purely based on their location, even if their $T_H$ is identical. The lower $T_C$ in Norway provides a slightly wider temperature "gap" to work with, illustrating that the environment itself places a boundary condition on efficiency calculations. ^[5]

In summary, the efficiency of any heat engine is fundamentally capped by the Second Law of Thermodynamics, which mandates that a portion of input heat must always be rejected to a colder reservoir. This theoretical maximum is quantified by the Carnot efficiency, which depends solely on the absolute temperatures of the hot source and the cold sink. Real-world engines fall short of this theoretical maximum due to irreversible processes like friction, heat transfer across finite temperature differences, and other mechanical losses. The pursuit of greater efficiency, therefore, becomes a dual challenge: striving for higher operating temperatures within the strict bounds set by material science, while simultaneously minimizing the unavoidable internal irreversibilities that degrade performance below the thermodynamic ceiling.^[1][2][7]