What is radial velocity NASA?

The concept of radial velocity sits at the heart of how astronomers track the movement of celestial bodies, particularly when searching for worlds orbiting distant stars. It is a fundamental measurement that tells us how fast an object—be it a star, galaxy, or a newly discovered exoplanet—is moving directly along our line of sight, either approaching us or receding from us. ^[2]^[8] NASA and partner agencies worldwide heavily rely on this principle to map the cosmos and characterize objects that are otherwise impossible to see directly. ^[3] Understanding radial velocity is essentially understanding motion through space as detected by the light these objects emit.

# Stellar Speed

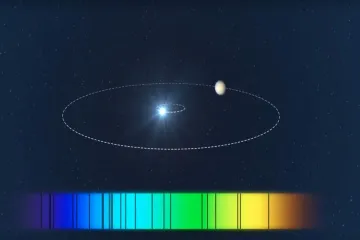
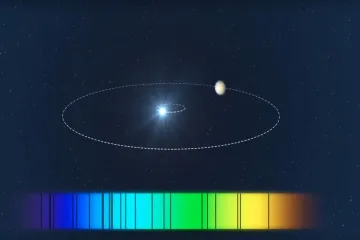
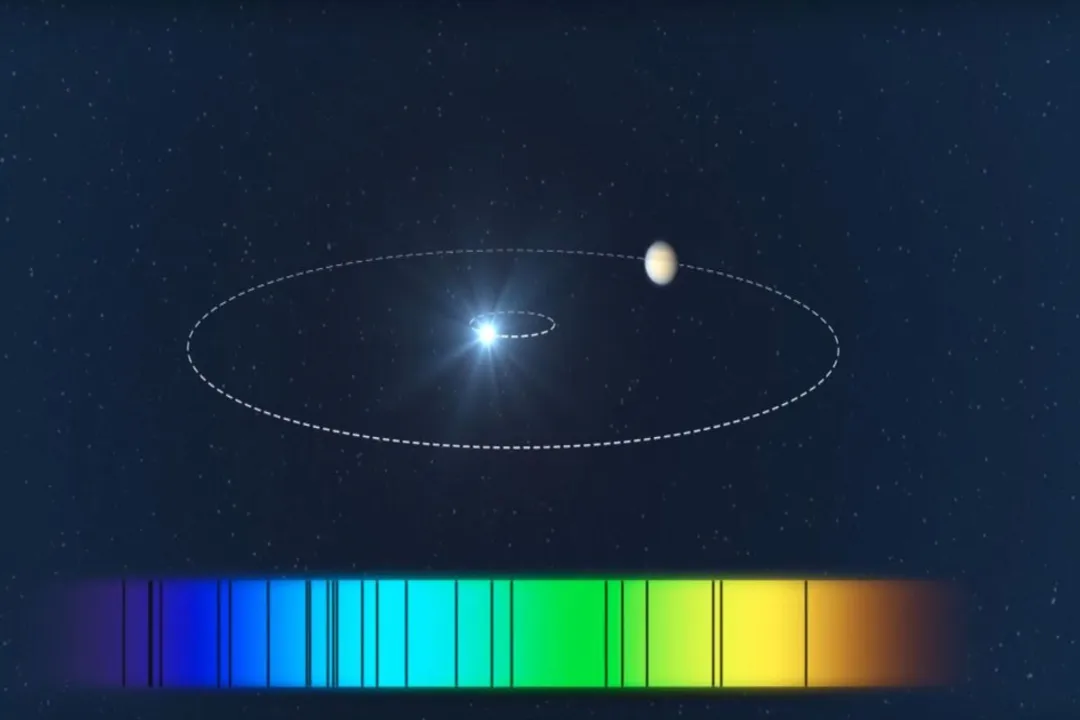
At its most basic, radial velocity is simply one component of an object’s total velocity vector. ^[8] We can measure a star’s speed moving across our field of view—its tangential velocity—but that is often extremely difficult for distant stars. What is much more accessible, thanks to the physics of light, is the speed along the line connecting the star to the observer, which is the radial velocity. ^[8] This measurement is crucial because when we look for exoplanets, we aren't usually seeing the planet itself; we are seeing the star react to the planet’s presence. ^[6] The gravitational interaction between a star and its orbiting companion causes the star to move slightly, a slight "wobble," as both orbit their common center of mass. ^[2]^[5] This minute back-and-forth motion, directed toward and away from Earth over time, is precisely what the radial velocity method seeks to capture. ^[6]

# Light Shift

The technique used to detect this motion relies on the Doppler effect, a phenomenon familiar to anyone who has heard a siren change pitch as an ambulance drives past. ^[2] For sound waves, the pitch changes based on whether the source is moving closer or further away. Light waves behave in the exact same manner. ^[10] When a star is moving toward the observer, the light waves it emits are compressed, causing the entire spectrum of light to shift slightly toward the blue end of the spectrum—this is known as blueshift. ^[2] Conversely, if the star is moving away from us, the light waves are stretched out, resulting in a redshift. ^[2]

Astronomers analyze a star's spectrum, which is crisscrossed by dark lines corresponding to specific elements present in the star's atmosphere (like hydrogen or calcium). ^[2] These spectral lines have very precise, known locations when the source is stationary relative to the observer. ^[10] By measuring how far these established lines have shifted in the observed spectrum, scientists can calculate the exact radial velocity of the star at that moment. ^[2]^[10] The magnitude of this shift is directly proportional to the star's speed along the line of sight. ^[10] NASA’s missions and ground-based observatories are built with instruments capable of detecting incredibly small shifts in these spectral lines, indicating velocity changes of just a few meters per second. ^[6]

# Planetary Tug

The radial velocity method, often called Doppler spectroscopy, is one of the original and most successful techniques for discovering exoplanets. ^[6]^[3] Imagine a star much more massive than Jupiter orbiting a planet. The planet exerts a tug on the star, making the star move in a small circle or ellipse around the center of mass. ^[2] As the star moves in this orbit, its radial velocity cycles predictably—it redshifts as it moves away, crosses zero velocity when moving perpendicular to our view, and then blueshifts as it moves toward us, repeating this cycle with the same period as the planet’s orbit. ^[5]^[6]

The resulting data plot, showing velocity versus time, produces a characteristic wave pattern. ^[5] The period of this wave tells us the orbital period of the unseen planet. The amplitude of the wave—how far the velocity shifts from its average—reveals crucial information about the planet.

It is worth noting that this method is particularly effective for finding massive planets orbiting close to their host stars. A more massive planet will cause a more substantial gravitational tug, resulting in a larger velocity oscillation that is easier to detect against the background noise of the star’s own natural movement. ^[2] For instance, detecting a Jupiter-sized planet orbiting a Sun-like star at an orbital distance similar to Mercury might result in a velocity change of about 13 meters per second, which is challenging but achievable with modern spectrographs. ^[6] Detecting an Earth-mass planet at the same distance would only cause a shift of about 9 centimeters per second, requiring instruments of far greater precision. ^[6]

# Inclination Problem

While the radial velocity method excels at determining the period and the minimum mass of a planetary companion, it suffers from a fundamental limitation dictated by geometry: we cannot know the exact angle of the orbit relative to our line of sight, known as the orbital inclination ( $i$ ). ^[5]^[8]

If a system is perfectly edge-on ( $i=90^\circ$ ), the star moves directly toward and directly away from us during its orbit. In this best-case scenario, the measured radial velocity matches the true orbital velocity, and the calculated mass ( $M_{\text{planet}}$ ) is accurate. ^[8] However, if the orbit is highly inclined (tilted, so $i$ is small, close to $0^\circ$ ), the star’s motion is mostly across our line of sight rather than along it. In this case, the measured radial velocity is only a fraction of the star's true orbital speed. ^[5]^[8]

Because the calculation yields only the minimum mass, $M \sin i$ , the true mass of the planet could be much larger if the system is tilted significantly away from our view. ^[5] For example, if the measured velocity corresponds to a 5 Jupiter-mass planet, but the system is actually tilted at a shallow angle, the true mass could be 10 or 20 times that of Jupiter. This inherent ambiguity is why astronomers often look for confirmation using the transit method, where a planet passing in front of its star causes a measurable dip in brightness. If a transit is detected, we know the system must be nearly edge-on ( $i \approx 90^\circ$ ), allowing the radial velocity measurement to provide the definitive mass. ^[3] The synergy between these two detection techniques paints a much clearer picture of the exoplanet's physical characteristics.

# Observing Tools

The precision required for radial velocity measurements demands highly specialized instrumentation, which NASA and its international partners invest in heavily. While some early data came from instruments on large ground-based telescopes, modern characterization often relies on cutting-edge spectrographs attached to powerful observatories. ^[6] These instruments must be exceptionally stable, as tiny temperature or pressure fluctuations within the instrument itself can mimic the minute Doppler shifts caused by a distant star’s wobble.

The sheer volume of data collected is also a factor. Since the technique relies on repeated measurements over months or years to establish the orbital period, an efficient system for cataloging and analyzing this data is essential. ^[5] NASA supports the Exoplanet Archive, which compiles information, including published radial velocity measurements, from numerous discovery papers, allowing researchers to access and compare established findings easily. ^[5] Beyond ground assets, space-based observations also play a role. While primarily known for surveying the sky, missions like the European Space Agency's Gaia spacecraft include radial velocity measurements in their offerings. Gaia is designed to precisely measure the distances and motions of billions of stars across the Milky Way, providing an enormous catalog of stellar kinematics, including radial velocities, which are vital for understanding galactic structure. ^[9]

# Future Data

The pursuit of ever more sensitive radial velocity measurements continues to drive instrument development. Future projects aim to push the detection limits down to Earth-mass planets orbiting Sun-like stars at Earth-like distances—the quintessential target for finding Earth 2.0. ^[6] Achieving this level of sensitivity requires instruments capable of measuring shifts down to centimeters per second, which is roughly the speed of a snail. ^[6]

The data collected through these efforts contributes to an increasingly detailed census of planetary systems. For instance, historical data points, such as those collected by instruments associated with early space missions, helped lay the groundwork for understanding stellar variability and how to filter out stellar noise from planetary signals. ^[10] As our technology improves, the ability to measure these tiny stellar movements with higher fidelity means we move closer to distinguishing between a massive gas giant and a rocky world based purely on the gravitational signature it leaves on its host star. ^[3] This relentless pursuit of precision in measuring light shifts is a cornerstone of modern astrophysics, offering indirect, yet powerful, insights into the nature of worlds light-years away. ^[1]^[4]