How does the radial velocity detection method work?

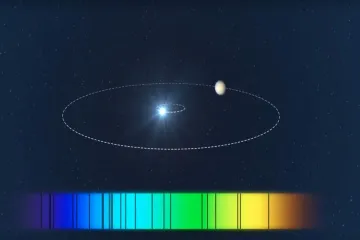
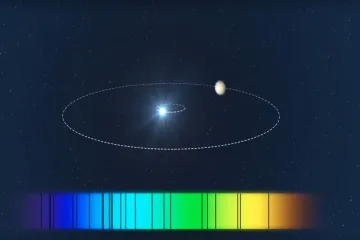
The seemingly steady light from a distant star is, in reality, rarely static. When we look across the vastness of space, we are often looking at an intricate cosmic dance, one that astronomers have learned to interpret by measuring minute shifts in that starlight. This process, known as the radial velocity (RV) method, is one of the foundational techniques that cracked open the field of exoplanet discovery, revealing worlds orbiting stars other than our Sun. ^[5][6] It is not a direct imaging technique; rather, it is an indirect measurement, relying on the gravitational consequences a planet exerts on its host star. ^[2]

# Gravitational Tug

A star and its orbiting planet do not orbit each other with the planet simply revolving around a fixed central point. Instead, both bodies orbit a shared center of mass, known as the barycenter. ^[2] Because the star is far more massive than the planet, the barycenter usually lies very close to, or even within, the star itself. However, this gravitational partnership forces the star to move in a small circle or ellipse around that barycenter. ^[5]

This movement causes the star to shift slightly back and forth along our line of sight—it moves sometimes toward us and sometimes away from us. ^[1][5] This phenomenon is the stellar "wobble" that the radial velocity method seeks to detect. ^[1][2] While this motion is tiny, often amounting to just a few meters per second, it is precisely this movement that gives away the presence of an unseen companion. ^[3]

# Light Shifts

To translate this physical wobble into measurable data, astronomers turn to a well-understood principle of physics: the Doppler effect. ^[3][5] We experience this effect every day with sound—the pitch of an ambulance siren rises as it approaches and drops as it moves away. Light behaves similarly. ^[1]

When a star is moving toward the Earth, the light waves it emits are compressed, causing their wavelengths to become slightly shorter. This phenomenon is called a blueshift. ^[1][3] Conversely, when the star is moving away from the Earth, its light waves are stretched, resulting in longer wavelengths, known as a redshift. ^[1][3][5]

The radial velocity method measures the precise degree of this shift. Since the light spectrum of any star is composed of thousands of distinct absorption lines—dark lines created when cooler atoms in the star's outer layers absorb light at specific wavelengths—these lines act as highly precise markers. ^[3] When the star wobbles toward us, all its spectral lines shift slightly toward the blue end of the spectrum; when it wobbles away, they all shift toward the red end. ^[1][3]

# Analyzing Spectra

The instrument crucial for this detection is the spectrograph, which functions much like a high-powered prism, spreading the star's light into a detailed spectrum. ^[3] High-precision spectrographs are required because the velocity changes we are looking for are minuscule, often on the scale of walking speed, which translates to shifts of only a few parts per million in the light's wavelength. ^[5]

Astronomers must first establish the star's rest velocity—its average velocity relative to Earth when it is not actively being tugged by a planet in an extreme part of its orbit. ^[2] Once this baseline is established, they monitor the spectral lines over time. ^[3] By carefully comparing the measured positions of these spectral features against known atomic reference patterns, scientists can calculate the star's instantaneous radial velocity. ^[2][3] The technique is sometimes called Doppler spectroscopy due to this reliance on measuring spectral shifts. ^[3]

If a planet is present, the resulting velocities plotted over time will trace out a periodic, repeating pattern—a smooth, wave-like function, specifically a sinusoid. ^[2][5] The period of this cycle corresponds exactly to the planet's orbital period. ^[2]

It is worth noting that while we measure the star's wobble, this method is fundamentally geared toward finding planets based on the star's reflected motion, not the planet's motion relative to the star. Because the star is hundreds or thousands of times more massive than the planet, the star moves much less than the planet does, but that tiny stellar movement is what is observable from light-years away. ^[2]

# Velocity Curves

The data collected from repeated measurements—the measured radial velocity versus time—is plotted to create a velocity curve. ^[5] For a simple, single-planet system seen edge-on, this curve will look like a perfect sine wave. ^[2]

The amplitude of this wave—how far the velocity swings from its average position (the maximum blueshift to the maximum redshift)—tells us something significant about the orbiting body. A larger amplitude means the star is moving faster, which implies that the planet is either more massive or orbiting closer to the star. ^[1][5]

If we consider a system where Jupiter orbits our Sun, the Sun's velocity variation is about $12.5 \text{ m/s}$. If we were observing a Sun-like star with an exoplanet causing a $50 \text{ m/s}$ wobble, we could immediately infer that the object causing the disturbance is significantly more powerful gravitationally than Jupiter is in our own system. ^[5] The ability to determine the period and the amplitude of this wobble provides the first concrete metrics for characterizing a newly found world. ^[2]

# Mass Ambiguity

Despite its success in detecting thousands of worlds, the radial velocity method has an inherent limitation tied directly to geometry: the problem of orbital inclination. ^[2][4]

When observing a star, we only know how much it is moving toward or away from us—the radial component of its motion. We cannot, from the Doppler shift alone, tell how much it is moving side-to-side in the plane of the sky (the tangential component). ^[2]

If a planetary system is perfectly face-on from our perspective, the star will only move side-to-side, and its velocity along the line of sight (the radial velocity) will be zero, meaning the RV method will fail to detect the planet entirely. ^[2][4] Conversely, if the system is perfectly edge-on, we see the full extent of the back-and-forth wobble, giving us the maximum possible velocity signal. ^[2]

Because we generally don't know the inclination ($i$) of a newly discovered orbit, the RV method only provides a lower limit on the planet’s mass, expressed as $M \sin i$. ^[2][4] If the star wobbles a lot, we know the planet is at least that massive. If the orbit happens to be highly inclined (nearly face-on), the true mass of the planet could be much larger than the calculated $M \sin i$ value.

This is where combining techniques becomes invaluable. If the RV method finds a planet, and the transit method (which requires an edge-on or near edge-on view to see the planet pass in front of the star) also detects a dip in brightness, we know the inclination $i$ is close to 90 degrees. In that scenario, $\sin i$ is nearly $1$, and the calculated minimum mass is very close to the true mass. ^[4] The existence of both signals together provides a wealth of information that neither method can offer alone. ^[4]

# Method Biases

The efficiency of the radial velocity technique is not uniform across all types of exoplanets; it exhibits distinct observational biases that shape the census of known worlds. ^[1] This systematic bias is important to understand when interpreting discovery statistics.

The sensitivity of the spectrograph dictates the smallest wobble it can reliably measure. Currently, this sensitivity favors the detection of massive planets orbiting relatively close to their stars. ^[1] Planets with orbital periods of just a few days or weeks produce large, rapid, and easily measurable velocity variations, meaning the star is quickly shifting back and forth many times a year.

A more massive object causes a larger signal, so "Hot Jupiters"—gas giants in close orbits—were among the first RV discoveries because they generate the largest shifts. ^[5] Finding smaller, Earth-mass planets requires incredibly precise measurement capabilities because their gravitational tug results in a much smaller stellar velocity change. For instance, detecting an Earth-like planet orbiting a Sun-like star would produce a wobble of only about $0.09 \text{ m/s}$—a measurement that was technologically impossible until the late 1990s and remains challenging today. ^[5]

If we imagine a star system with a planet the size of Neptune orbiting at the distance of Mars, the resulting RV signal would be so small and the orbital period so long (years) that it could easily fall below the detection threshold for current instruments, or require decades of sustained observation to confirm the periodicity of the curve. ^[1] This inherent sensitivity means that the RV survey results are skewed toward finding high-mass planets in short-period orbits, rather than an unbiased sample of all existing planetary types. ^[1]

# Long Observations

One key distinction between the RV method and the transit method (which relies on a brief blackout) is the time commitment. While a transit might occur over a few hours, confirming an RV signal often requires sustained monitoring over many months or even years to accurately map out the full sinusoidal curve and rule out other astrophysical noise sources. ^[5]

Astronomers must account for noise that isn't caused by planets. Stars are not perfectly uniform light sources; they have magnetic activity, such as starspots (like sunspots), which rotate across the star's surface and modulate the light in ways that can mimic a planetary signal. ^[6] Distinguishing between a real planet and stellar activity requires extensive, time-consuming observation campaigns where the pattern of noise is characterized and subtracted from the overall velocity measurement. ^[6]

In practice, the initial detection often involves finding a few significant shifts suggesting a planet, followed by years of follow-up observations to confirm that the pattern repeats with the same period and amplitude, thereby confirming it as an orbital signature rather than a random stellar event. This diligence is what builds the trust in the final catalogue of confirmed exoplanets. ^[5]

To put the required precision into perspective, consider the difference between the gravitational tug of a Jupiter-mass planet and a Mars-mass planet around a Sun-like star. Jupiter's gravitational influence creates a velocity amplitude of about $12.5 \text{ m/s}$. ^[5] In contrast, a Mars-mass planet would induce a wobble closer to $0.1 \text{ m/s}$. ^[3] The difference in required measurement accuracy between these two scenarios is over 100 times, highlighting why the RV catalog historically dominated with larger, closer worlds before next-generation spectrographs became available.

Planet Type (Orbiting Sun-like Star)	Approximate Radial Velocity Amplitude ($\text{m/s}$)	Detection Difficulty (RV)
Jupiter	$\approx 12.5$	Relatively straightforward
Neptune	$\approx 2.7$	Challenging, requires long monitoring
Earth	$\approx 0.09$	Extremely difficult, requires world-class precision
Mars	$\approx 0.04$	Currently beyond routine capability

This table illustrates that the RV method is inherently biased toward detecting systems where the planet's gravity has a relatively large effect on the visible star. While advancements in instrumentation continue to push this detection threshold lower, it remains a significant factor in how we perceive the exoplanet population discovered via this technique. ^[1] This is why methods looking at the star's size (transits) remain a necessary complementary approach for finding smaller, more Earth-like worlds.

# Future Applications

The radial velocity method isn't just about finding large planets close in; it continues to evolve. Next-generation spectrographs are becoming sensitive enough to target smaller, longer-period planets, inching closer to the realm of Earth analogs. ^[5] Furthermore, the technique remains the only reliable way to estimate the true mass of planets found via the transit method, allowing scientists to calculate the crucial bulk density when both radius (from transit) and mass (from RV) are known. ^[4] Understanding density—whether a world is rocky like Earth or gaseous like Neptune—is fundamental to determining its habitability potential. ^[4] Even as transit surveys discover exponentially more worlds, the precision required for the RV method ensures it remains the gold standard for mass measurement in exoplanet science. ^[6]