What is the radial velocity Doppler method?
The search for worlds beyond our solar system fundamentally relies on detecting the subtle effects these unseen companions have on their parent stars. Among the most successful and historically significant ways to achieve this is the radial velocity method, often referred to as Doppler spectroscopy. [1][9] Instead of looking for a planet passing in front of its star—which is a different technique—this method looks for the star itself moving back and forth, a tiny cosmic dance induced by the gravitational tug of an orbiting planet. [2][3]
# Star Wobble
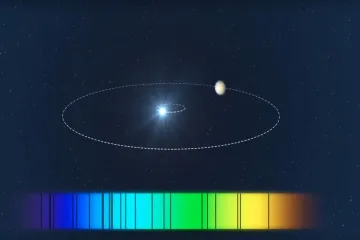
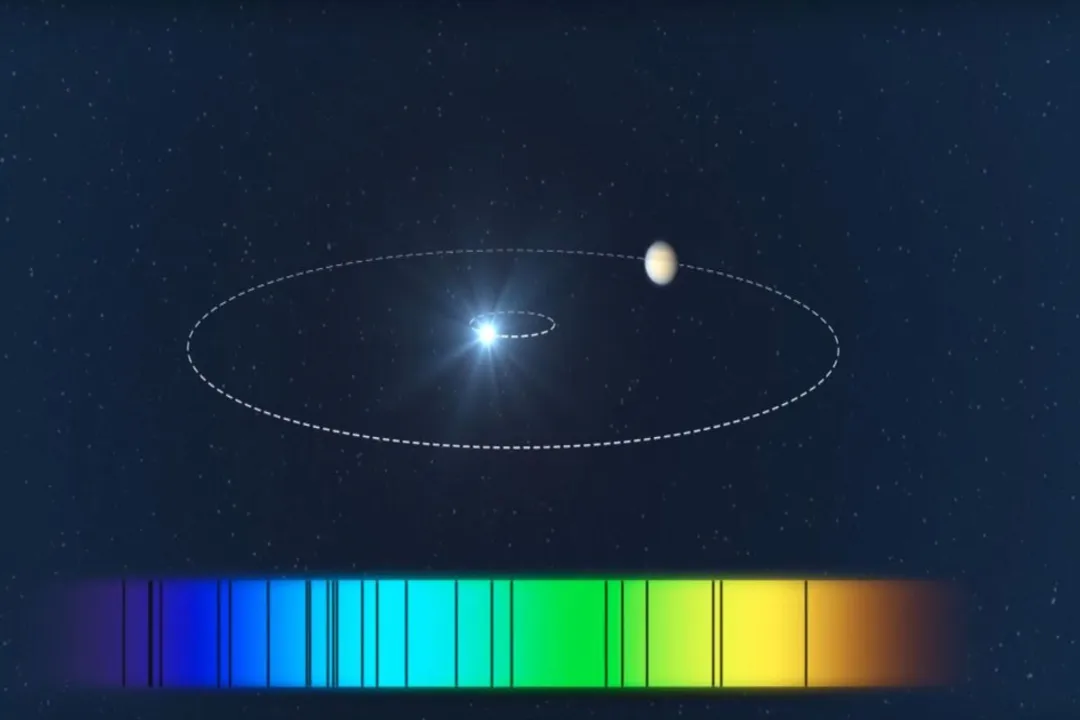
The entire premise hinges on a simple but profound physical reality: planets do not orbit their stars neatly. While we often picture the Earth circling the Sun in an isolated path, the Sun is also pulled by the Earth’s gravity. [3] In reality, both the star and the planet orbit a common center of mass, known as the barycenter. [5][7] Because stars are vastly more massive than planets, this barycenter is almost always located inside the star itself. [5] However, the star still shifts its position slightly as it orbits this central point. [1][3]
This slight orbital motion causes the star to move slightly toward Earth and then slightly away from Earth over the course of one orbit. [2] This movement is what astronomers call the "wobble". [2] It is the detection of this periodic back-and-forth motion along our line of sight—the radial velocity—that reveals the presence of the unseen planet. [1][7]
# Doppler Physics
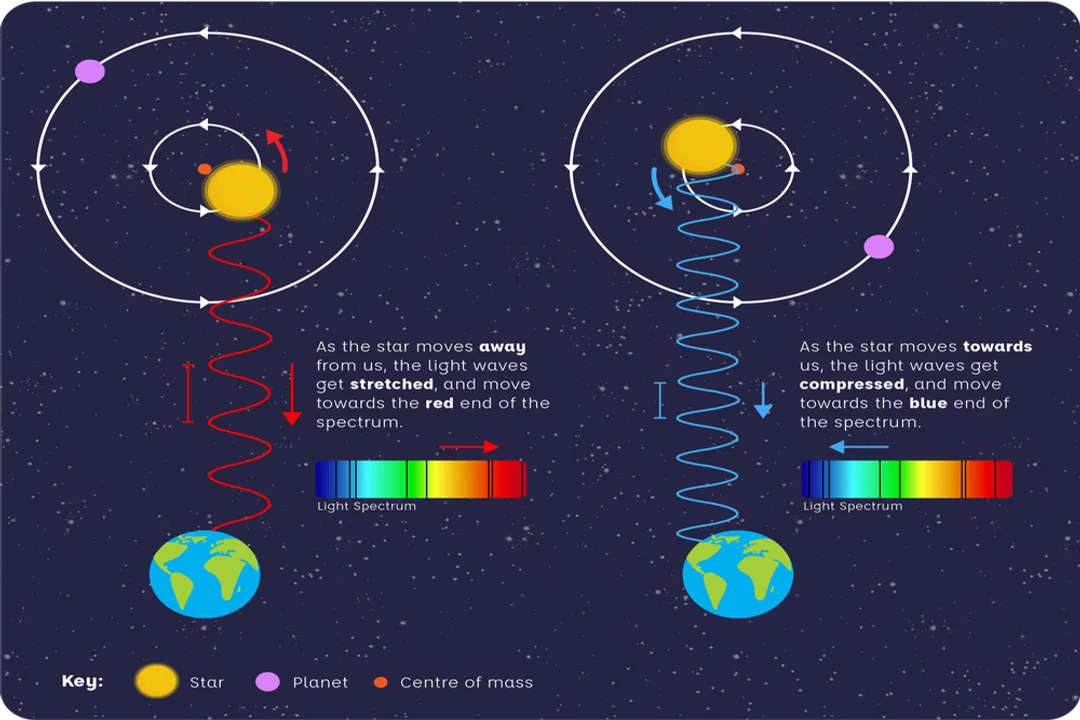
The physical principle that makes this detection possible is the Doppler Effect. [5] Most people are familiar with this effect from sound waves: an ambulance siren sounds higher pitched as it approaches and lower pitched as it moves away. [2] Light exhibits the exact same phenomenon. [5]
When the star is moving toward an observer on Earth, the light waves it emits are compressed, causing their wavelength to shift toward the shorter, bluer end of the electromagnetic spectrum—a phenomenon called blueshift. [2][5] Conversely, when the star is moving away from Earth, the light waves are stretched, shifting their wavelength toward the longer, redder end of the spectrum, known as redshift. [2][5]
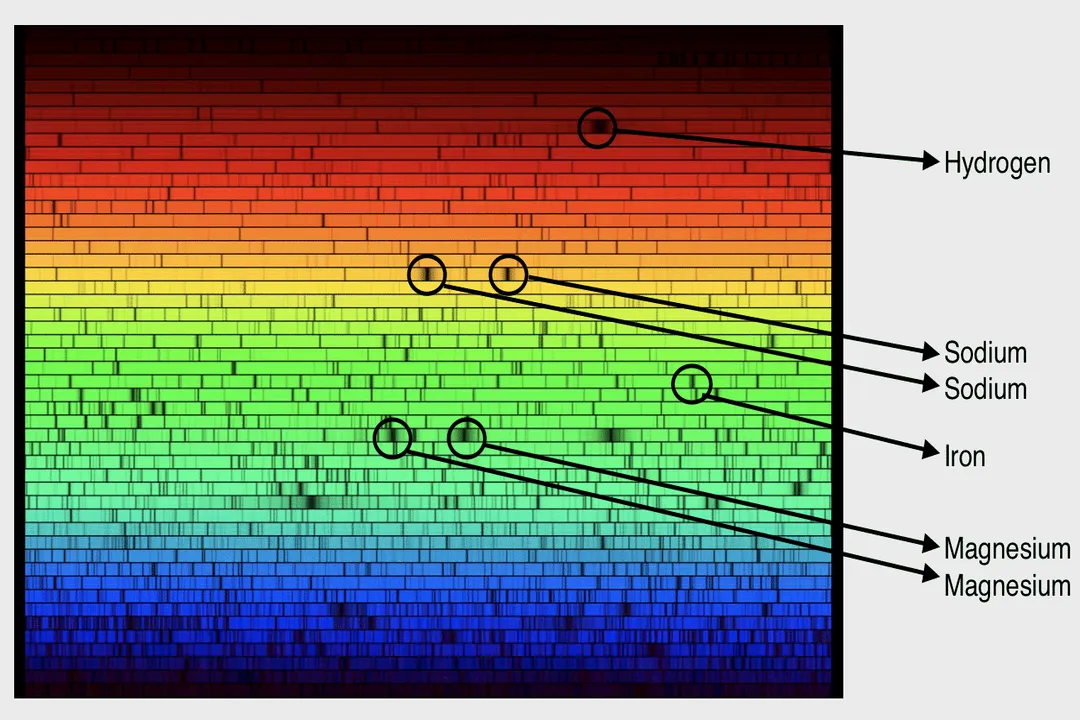
To detect this minute shift in a star hundreds of light-years away requires incredibly precise tools, specifically high-resolution spectrographs. [1][3] A spectrograph splits the starlight into its constituent colors, creating a spectrum that reveals specific dark lines called absorption lines. [5] These lines are like the star’s unique fingerprint, caused by specific elements in the star’s atmosphere absorbing light at precise wavelengths. [3] If the star moves, all of these absorption lines shift in unison toward the red or blue end of the spectrum. [2] The degree of this shift, measured in mere fractions of the speed of light, tells the astronomer the radial speed of the star at that moment. [1][7]
# Mapping the Motion
Observing a radial velocity signal is not a one-time event; it requires sustained monitoring of the star over many months or years. [3][9] Astronomers repeatedly measure the star’s spectrum, logging the measured shift (the radial velocity) against the time of observation. [1] When plotted on a graph, these data points typically form a characteristic S-shaped curve, or, for a single orbiting planet, a smooth sinusoidal curve. [5][9]
This curve is the direct readout of the star’s movement around the barycenter. [3] If a planet is present, the star will approach for half an orbit (blueshift), reach its maximum speed away from us (redshift), and then return. [2] The time it takes for the star to complete one full cycle—returning to the same point on the curve—is the orbital period of the planet. [1][5]
# Instrumental Precision
The precision required for this work is staggering. For a star like our Sun, the gravitational tug of a Jupiter-sized planet orbiting at the distance of Earth would cause the Sun to wobble at only about 13 meters per second (about 29 miles per hour). [2][3] Detecting a smaller, Earth-sized planet orbiting at the same distance requires measuring speeds as low as 9 centimeters per second (about 0.2 miles per hour). [3][9]
This need for extreme accuracy has driven engineering innovation in ground-based telescopes. Consider the spectrographs themselves. A critical factor in the success of modern RV surveys is not just the size of the telescope, but the stability of the instrument itself. [10] If the instrument's own components subtly expand, contract, or shift due to temperature changes or vibrations, the resulting "wobbles" in the measured spectrum could be larger than the actual stellar signal. [1] Modern instruments often use complex calibration systems, such as laser frequency combs, to create incredibly stable reference points against which the stellar lines can be measured, ensuring that the detected shifts are truly astronomical and not terrestrial artifacts. [1] This obsessive control over instrumental drift is where much of the expertise in the field lies. [10]
# Planetary Attributes
The radial velocity method is powerful because it allows astronomers to derive fundamental properties of the exoplanet, provided they can observe a complete orbit. [1][7]
The shape and amplitude of the velocity curve yield two key parameters:
- Orbital Period (P): This is simply the time taken to trace one full cycle of the curve. [1][5]
- Velocity Amplitude (K): This is the maximum radial speed reached by the star, which corresponds to half the peak-to-trough height of the sine wave. [1][5]
From these two pieces of data, astronomers can calculate the semimajor axis (average orbital distance) using Kepler’s Third Law, if they know the mass of the host star. [1][7]
However, the method has a significant limitation built into its geometry. The Doppler shift only measures motion along the line of sight. [3] If a planetary system is oriented so that the planet orbits perfectly edge-on to our view, we see the maximum possible motion, and the RV measurement gives us the true mass of the planet. [1][3]
If the orbit is highly inclined—tilted away from our view—we only measure a component of the star's true velocity, meaning the calculated mass will be an underestimate. [1][3] Therefore, the RV method directly yields a measurement of the planet's mass multiplied by the sine of the inclination angle (), resulting in the minimum mass () of the orbiting body. [1][4][7]
Where is the period, is the radial velocity amplitude, is the gravitational constant, and is the star's mass. [1] This equation highlights the dependence on the unknown inclination (). [1] A planet detected by RV alone is often reported with its minimum mass because the inclination is unknown unless another technique, like the transit method, confirms a crossing. [4]
# Comparing Strengths and Weaknesses
The radial velocity technique was, alongside the transit method, responsible for the initial explosion in exoplanet discoveries starting in the mid-1990s. [9] Its strength lies in its ability to detect planets orbiting a wide variety of stars, including those that do not transit. [3] Furthermore, because it relies on the star's motion, it is particularly adept at finding massive planets close to their stars—the "hot Jupiters"—because these systems induce the largest and fastest stellar wobbles. [5][9]
The historical advantage of RV over the transit method for early discoveries was that it did not require the planet to pass directly between the star and the Earth; only a slight angular offset in the orbital plane was needed to see some radial velocity signal. [3]
However, the technique faces several challenges that can sometimes be circumvented by the transit method.
| Feature | Radial Velocity Method | Transit Method |
|---|---|---|
| What is measured? | Stellar light shifts (Doppler Effect) [2] | Stellar brightness dips [3] |
| Data Output | Orbital period, Minimum Mass () [1] | Orbital period, Planet Radius, Orbital Inclination () [3] |
| Ideal Target | Massive planets close to the star [5] | Planets whose orbits are perfectly edge-on to us [3] |
| Stellar Noise | Sensitive to starspots, stellar activity, oscillations [1] | Less sensitive to stellar activity if spots are small relative to planet |
A significant hurdle for RV is stellar noise. [1] Stars are not perfect light sources; they have magnetic activity, such as starspots (the stellar equivalent of sunspots). [1] These spots rotate in and out of view, changing the star's observed spectrum and mimicking or masking the tiny signal from a planet. [1] Astronomers must spend significant time modeling and subtracting this stellar activity, which can sometimes obscure the planet's signal entirely, especially for smaller worlds or stars with high magnetic fields. [1] In fact, differentiating between a small planet and a subtle change in the star's rotation rate can be a major source of uncertainty in published results, which often leads to papers reporting lower bounds or statistical likelihoods rather than definitive masses. [6]
An interesting technical comparison stems from this noise. While the transit method loses data if the planet doesn't transit, the RV method suffers if the star hides its movement beneath its own activity. For a Sun-like star, a Jupiter-mass planet causes a wobble. A large, cool starspot rotating across the star’s face can induce apparent velocity changes of similar magnitude, making a definite detection difficult unless observations span multiple years to confirm the periodicity is indeed planetary. [1]
# Future Horizons
The radial velocity method continues to evolve, pushing the boundaries of precision to find smaller and smaller worlds. [6] While early successes targeted Jupiter-sized planets, current and future instruments are designed to detect Earth-mass planets orbiting Sun-like stars. [3] This quest demands instruments with unprecedented stability, moving from measuring velocity changes in the tens of meters per second down to the centimeter-per-second range. [10]
Furthermore, combining RV data with transit data offers the best of both worlds. If a planet is observed to both transit (providing radius and inclination ) and exhibit a measurable Doppler shift (providing ), astronomers can solve the equation for the true mass () and calculate the planet’s bulk density. [4] This density is a crucial clue to a planet's composition—whether it is rocky, gaseous, or an icy giant. [4]
The technique remains a foundational tool in exoplanetary science. It provided the first robust evidence that planets are common around other stars, setting the stage for the billions of worlds we now know exist across the galaxy. [9] It is the gravitational detective work that first revealed the cosmic dance of distant systems, proving that the stars we see are not solitary beacons, but the anchors for entire families of unseen companions. [2]
#Videos
Observatory Online: Exoplanets and the Radial Velocity Method
Related Questions
#Citations
Doppler spectroscopy - Wikipedia
Color-Shifting Stars: The Radial-Velocity Method
Radial Velocity Method - Las Cumbres Observatory
Radial Velocity Planet Resources in the Exoplanet Archive
7.3: The Doppler Technique - K12 LibreTexts
[2410.11424] Radial velocity technique - arXiv
Radial-Velocity Method - an overview | ScienceDirect Topics
The radial velocity method for finding exoplanets - ESO.org
What is the Radial Velocity Method? - Universe Today
Observatory Online: Exoplanets and the Radial Velocity Method