Why do black holes evaporate via Hawking radiation?
The notion that black holes, objects defined by a boundary from which nothing, not even light, can escape, are actually emitting radiation and slowly shrinking over eons seems counterintuitive, yet it is a profound prediction born from combining general relativity with quantum mechanics. [3][4] Stephen Hawking proposed this mechanism in the mid-1970s, demonstrating that black holes are not entirely black but instead possess a faint thermal glow, a process termed Hawking radiation. [3]
# Vacuum Fluctuations
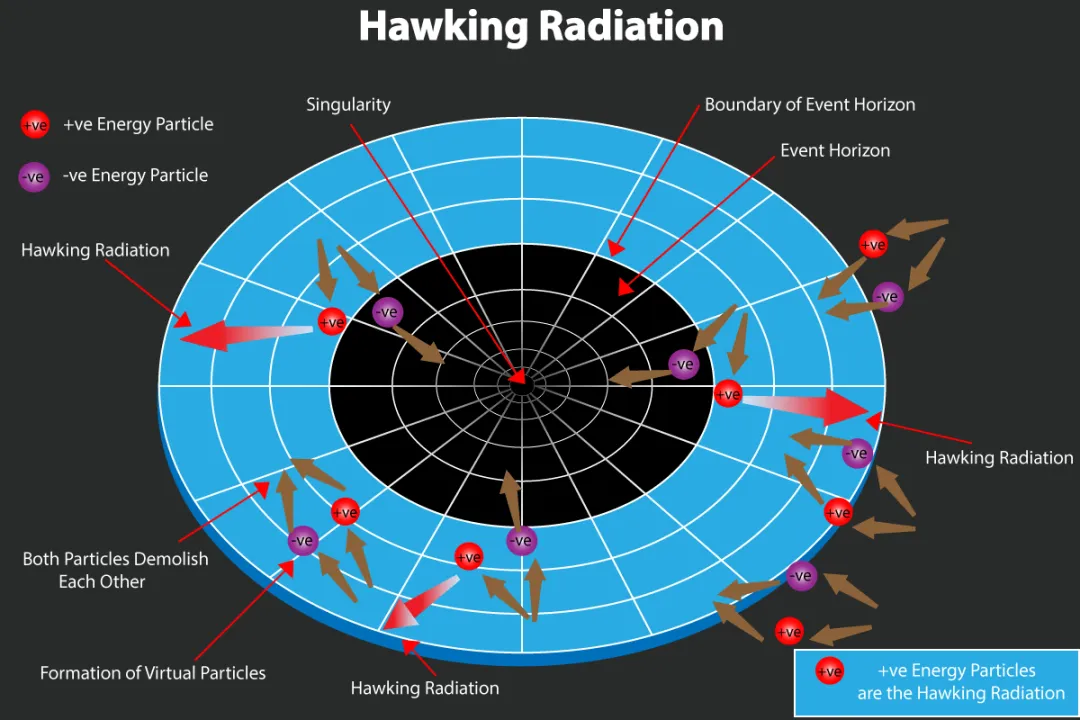
To grasp how something escapes a point of no return, one must look not at the black hole itself, but at the seemingly empty space surrounding it. [3] According to quantum mechanics, the vacuum of space is not truly void; it is a frothing sea of activity where virtual particle-antiparticle pairs constantly blink into existence and annihilate each other almost instantaneously. [3][6] These pairs exist for such fleeting moments that they cannot be directly observed in isolation, but their effects are measurable. [3]
These pairs, such as an electron and a positron, carry equal and opposite energy, ensuring that energy conservation is maintained during their brief existence. [3] In normal, flat spacetime, this balancing act proceeds without incident, and the pairs vanish back into the quantum foam. [3]
# Horizon Dynamics
The situation changes dramatically when these virtual pairs materialize right at the boundary of a black hole: the event horizon. [5] The intense gravitational gradient near this boundary can sometimes pull the pair apart before they have a chance to recombine. [3][5]
When this separation occurs precisely at the horizon, one particle might cross the boundary and fall into the black hole, while the other manages to escape to a distant observer. [3][5] The escaping particle is detected as Hawking radiation. [2][3]
The critical subtlety here involves energy and momentum. To an observer located far away from the black hole, the particle that falls into the horizon effectively carries negative energy relative to that distant frame of reference. [1][2][5] Because energy must be conserved for the overall system (the black hole plus the escaping particle), the positive energy carried away by the escaping radiation must be balanced by the negative energy absorbed by the black hole. [1][5]
It is this absorption of negative energy by the black hole that results in a corresponding loss of mass and, consequently, the evaporation process. [1][2] The escaping particle is the radiation, and the infalling particle carries the deficit needed to reduce the black hole’s mass, . [2] It is not that the particle is outrunning the speed of light to escape the event horizon, but rather that the energy exchange permitted by the extreme geometry dictates the mass loss. [5]
# Energy Balance
This mechanism is fundamentally a semi-classical description of gravity; it employs general relativity to describe the curved spacetime of the horizon while using quantum field theory to describe particle creation. [4] If we examine the process from the perspective of the black hole itself, it must emit particles matching its own temperature, meaning the radiation it gives off is thermal. [3] This temperature is intrinsically linked to the black hole's characteristics, specifically its surface gravity, which is directly related to its mass. [3]
One interesting point that arises from analyzing the math—and this is something often overlooked in simplified explanations—is that the energy lost by the black hole to create a real particle pair is equivalent to the energy gained by the universe in the form of the escaping particle. [2][9] Imagine the black hole as an incredibly dense reservoir; by effectively lending negative energy to the infalling partner, it reduces its own principal balance, allowing the positive-energy partner to exist freely in the cosmos. [1]
If you were to construct a simple table illustrating the relationship between mass and the resultant radiation profile, it highlights the extreme nature of this process for different cosmic objects:
| Black Hole Type | Approximate Mass () | Relative Temperature | Evaporation Timescale (Years) |
|---|---|---|---|
| Supermassive (Galaxy Center) | $10^8$ | Extremely Low | |
| Stellar Mass (Formed from star) | $10$ | Very Low | |
| Primordial (Hypothetical, small) | kg () | High |
While the math confirms the mechanism, it is worth noting that a black hole the mass of our Sun would take approximately years to fully evaporate. [1][3][4] Given that the universe is currently only about years old, the evaporation of even stellar-mass black holes is an event far outside humanity's conceivable future, residing deep in the cosmological dark ages. [3]
# Temperature Relation
The defining characteristic of Hawking radiation is that its temperature () is inversely proportional to the black hole's mass (). [1][3] This means that smaller black holes are hotter and radiate much more intensely than larger ones. [3]
This relationship dictates the speed of evaporation. A massive black hole, like one residing at the center of a galaxy, has an infinitesimally small temperature, meaning the rate at which it loses mass through radiation is negligible compared to the rate at which it consumes surrounding matter (like gas or stars). [3] For these behemoths, they are actively growing, not evaporating. [3]
Conversely, a very small, hypothetical primordial black hole—one formed in the early, high-energy conditions of the Big Bang—would be exceedingly hot. [3] If such a black hole had a mass around kilograms (far less than an asteroid), it would evaporate in a spectacular burst in a time frame closer to the current age of the cosmos, around years. [3] These small ones are the only ones that could feasibly complete their lifecycle via Hawking radiation within the universe's observable future. [3]
# Cosmic Timelines
The evaporation process follows a runaway path. As the black hole loses mass, its temperature increases, which causes it to lose mass even faster—a positive feedback loop of decay. [3] This accelerating decay means that the final moments of a black hole’s life would be a massive, incredibly energetic burst of high-energy particles, effectively ending its existence in a flash. [3][4]
Considering the stability of large black holes, it is a fascinating exercise to put their longevity into perspective. If we take a solar-mass black hole and compare its predicted evaporation time ( years) against the time remaining until the universe hits its "heat death" (estimated to be vastly larger, involving the decay of protons and the eventual cold dispersal of all matter), we can see that the black hole will likely outlast almost everything else in the cosmos, only to finally vanish in its final, energetic sputtering. [4] This places them as some of the longest-lived structures in the universe, ironically only destined for true extinction via this quantum process that seems so minor on astronomical scales. [1]
# The Core Question
A common follow-up question focuses on the singularity itself: How can the infinitely dense point at the center evaporate if its gravity is inescapable? The key takeaway here is that Hawking radiation is a phenomenon defined by the event horizon, not the singularity. [9] The process happens outside the singularity, in the region governed by the curvature of spacetime immediately bordering the horizon. [9]
While the classical description of a black hole suggests a singularity, a full theory of quantum gravity—which we do not yet possess—would likely smooth out or resolve this infinite density point. [9] However, for the purposes of the Hawking radiation calculation, the singularity's internal mechanics are irrelevant to the external emission; the energy loss is calculated purely based on the mass contained within the horizon and the external quantum field effects near that boundary. [9] The radiation dictates the decrease in the black hole's mass parameter, which in turn dictates the properties of the horizon over time, regardless of what state the infinitely compressed remnant material inside might be in. [9] The evaporation is a macroscopic effect dictated by the boundary conditions imposed by quantum fluctuations near that boundary.
#Videos
Hawking Radiation explained simply, or How black holes explode!
Related Questions
#Citations
Hawking's radiation and black holes evaporation : r/AskPhysics
How exactly does Hawking radiation decrease the mass of black ...
How do black holes evaporate from Hawking radiation? - Big Think
Black hole evaporation: Theoretical study proves Stephen Hawking ...
How does Hawking radiation escape the event horizon, thus making ...
Understanding Hawking Radiation and Black Hole Evaporation
Hawking Radiation explained simply, or How black holes explode!
Black Holes Evaporate--Now Physicists Think Everything Else Does ...
How do infinitely dense singularities evaporate through Hawking ...

