What is the relationship between the distance of an object and its redshift?

When we look out into the cosmos with powerful telescopes, we are not just seeing objects as they are now, but as they were when the light left them long ago. The primary tool astronomers use to gauge just how far away these distant sources are is a phenomenon called redshift. This measurement links directly to the expansion of the universe, providing a crucial yardstick for mapping cosmic distances and understanding the universe’s history. ^[6]

# Defining Shift

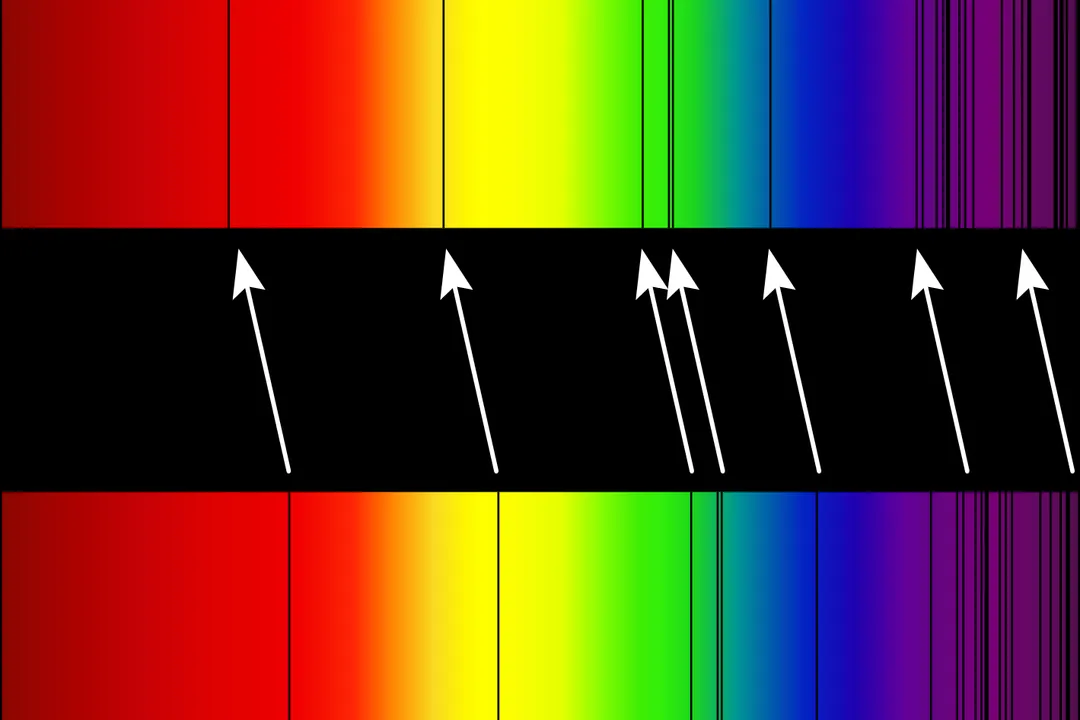
At its most fundamental, redshift, symbolized by the letter $z$, describes a change in the wavelength of light received from a source compared to the wavelength emitted by that source. ^[8] If the observed wavelength is longer than the emitted wavelength—shifting it toward the red end of the electromagnetic spectrum—it is called a redshift. ^[8] Conversely, if the wavelength is shorter, it is termed a blueshift.

The mathematical definition for redshift is straightforward: it is calculated as the difference between the observed wavelength ($\lambda_{obs}$) and the emitted wavelength ($\lambda_{emit}$), divided by the emitted wavelength: $z = (\lambda_{obs} - \lambda_{emit}) / \lambda_{emit}$. ^[8] For instance, if a specific spectral line that we know emits light at $500$ nanometers appears to us at $600$ nanometers, the redshift $z$ would be $(600-500)/500$, or $0.2$. ^[8]

It is essential to recognize that not all redshifts are created equal. There are three primary causes for this stretching or shifting of light. ^[8] The first is the Doppler effect, which occurs when a light source is moving relative to the observer through space—a standard effect we observe with sound waves, too. The second is gravitational redshift, which occurs when light climbs out of a strong gravitational well, losing energy in the process. ^[8] However, when we discuss galaxies millions or billions of light-years away, the dominant and most cosmologically significant effect is the cosmological redshift. ^[3][8]

# Cosmic Expansion

The cosmological redshift is fundamentally different from the Doppler shift because it is not caused by the galaxy moving through space, but rather by the expansion of space itself between the source and the observer. ^[3] Imagine drawing dots on a rubber sheet and then stretching the sheet; the dots move apart, not because they walked, but because the medium connecting them grew larger. ^[3]

This stretching causes the wavelength of the photons traveling through that space to stretch proportionally to the expansion that has occurred during their journey. ^[3][5] Therefore, the farther away an object is, the longer its light has traveled, and the more the space it traversed has expanded. ^[5] This is why a greater redshift ($z$) directly correlates with greater distance and, consequently, the object’s light being emitted further back in cosmic time. ^[5] If we look at a very distant quasar with a high redshift, we are seeing light that has been subjected to a massive amount of cosmic expansion along its path. ^[5]

While the cosmological redshift dominates for distant galaxies, for objects within our local group, like the Andromeda Galaxy, the measured redshift is actually a blueshift, indicating local gravitational or bulk motion that overrides the slight uniform expansion we see over vast scales. ^[8] This contrast helps illustrate the different physical mechanisms at play: local motions cause Doppler shifts, while the stretching of the cosmos causes the cosmological shift observed for receding galaxies. ^[8]

Why does redshift increase with distance?

# Hubble's Law

For relatively nearby galaxies—those where the recession velocity is much less than the speed of light—the relationship between distance and redshift becomes remarkably linear. This direct proportionality is formalized as Hubble’s Law. ^[1] The law states that the recession velocity ($v$) of a galaxy is proportional to its distance ($d$) from us. ^[1][4] Mathematically, this is written as $v = H_0 d$. ^[1]

The proportionality constant, $H_0$, is the Hubble Constant, which describes the current rate of the universe's expansion. ^[1] When astronomers measure the redshift ($z$) of a nearby galaxy, they first convert that redshift into a velocity ($v$) using approximations based on the Doppler effect formula, and then use the known value of $H_0$ to estimate the distance ($d$). ^[4]

For small redshifts ($z \ll 1$), the velocity $v$ can be approximated as $v \approx cz$, where $c$ is the speed of light. ^[2] Substituting this into Hubble’s Law, we get a simple expression for distance: $d \approx cz / H_0$. ^[2] This approximation is incredibly useful for mapping the nearby universe, providing a practical method to turn a spectral observation ($z$) into a physical distance ($d$). ^[4]

However, the precise, universally accepted value of the Hubble Constant remains a subject of active scientific debate, often referred to as the "Hubble Tension". ^[2] Different measurement techniques yield slightly different values for $H_0$ (e.g., values around $70\ \text{km/s/Mpc}$ derived from the Cosmic Microwave Background versus slightly higher values from local Type Ia supernovae observations). ^[2] This discrepancy means that even if we measure a perfect redshift, the exact distance calculated depends on which accepted value of $H_0$ we plug into our equation. For example, if $H_0$ is slightly smaller, the implied distance for the same redshift must be larger, suggesting a slightly different expansion history. ^[2]

# Limits of Linearity

Relying on the simple linear form of Hubble’s Law ($v = H_0 d$ or $d \approx cz/H_0$) works very well for nearby objects where the redshift is small, perhaps $z$ less than $0.1$ or $0.2$. ^[7] However, as we look at increasingly distant objects, such as quasars or early galaxies, the redshift becomes significant—$z$ might be $1$, $2$, or even higher. ^[7]

When $z$ gets large, the approximation breaks down because the universe's expansion rate has not been constant over the entire history of the light travel time. ^[7] The relationship between distance and redshift is not purely linear across the vastness of cosmic time. The equation $d \approx cz/H_0$ fails because it ignores the deceleration caused by matter and the acceleration driven by dark energy. ^[7]

To accurately determine the distance to a high-redshift object, cosmologists must employ the full set of Friedmann equations derived from general relativity, which incorporate the densities of matter ($\Omega_m$), radiation, and dark energy ($\Omega_{\Lambda}$). ^[7] These models describe how the expansion rate changes over time. Therefore, while redshift fundamentally measures how much space has expanded, converting that expansion factor ($z$) into a physical distance ($d$) requires a complete model of the universe's composition. ^[7] An object with a very high redshift ($z \approx 10$) tells us that the scale factor of the universe has increased by a factor of $(1+z)$, but the precise lookback time or proper distance depends on that complete cosmological narrative. ^[7]

What is the most accurate way to measure distance?

# Measuring Distance

The practical process of determining how distance relates to redshift involves precise astronomical measurements of spectral lines. ^[9] Every element, like hydrogen or oxygen, has unique spectral signatures—specific wavelengths of light it absorbs or emits. ^[8]

The observation procedure generally follows these steps:

1. Identify a Spectral Line: Astronomers observe the spectrum of a distant galaxy and identify a known emission or absorption line (e.g., the Hydrogen-alpha line, which should be at $656.3\ \text{nm}$ if stationary). ^[8]
2. Measure Observed Wavelength: The actual wavelength where this line is detected in the telescope's data is recorded ($\lambda_{obs}$). ^[8]
3. Calculate Redshift ($z$): The value of $z$ is computed using the standard formula. ^[8]
4. Determine Velocity (for low $z$): If $z$ is small, the velocity $v$ is approximated as $cz$. ^[2]
5. Calculate Distance: Using the Hubble Constant ($H_0$) and the derived velocity (or the redshift directly via the full cosmological model), the distance ($d$) is estimated. ^[4][2]

This technique is why redshift surveys are so informative; they allow us to build three-dimensional maps of the large-scale structure of the universe, showing where clusters and voids lie relative to one another based on their measured recession velocities. ^[9] The relationship is so foundational that redshift effectively serves as the most practical distance indicator for anything outside our immediate galactic neighborhood. ^[6] The ability to measure redshift accurately is what propelled many key discoveries, including the realization that the universe is expanding in the first place. ^[3]

# Analyzing Distance Markers

The fact that redshift scales with distance means we can use certain types of objects as standard rulers or candles, even if the direct distance calculation is complex. Consider two hypothetical galaxies: Galaxy A has $z=0.05$, and Galaxy B has $z=0.1$. Assuming we are in the region where the linear approximation holds reasonably well, Galaxy B is approximately twice as far away as Galaxy A, because its light has been stretched twice as much by the intervening expansion. ^[5]

When considering the limitations of the linear model, it is worth contemplating the apparent paradox of the $13.6$ billion light-year limit mentioned in discussions about high redshifts. ^[7] The observable universe has a physical radius that is much larger than the distance light has traveled (the lookback time) because space has continued to expand while the light was on its way. A galaxy that emitted light when the universe was very young (and thus appears at a high redshift) could now be located much further away due to the subsequent expansion of the intervening space. ^[7] The linear formula ($d = cz/H_0$) only gives an estimate of the distance at the time the light was emitted (or a very rough approximation of the current proper distance), which is why the full $\Lambda\text{CDM}$ cosmological model is necessary for precision. ^[7] The key takeaway is that redshift is inherently a measure of expansion factor, and converting that factor into a current physical distance requires knowing the ingredients (matter, dark energy) that dictate the rate of that expansion over time. ^[7]