What are the three main measurements?
The concept of the "three main measurements" shifts its meaning depending entirely on the context—whether we are discussing the foundational units of the universe as understood by physics, the basic dimensions used to describe physical space, or the most essential metrics tracked in applied fields like healthcare or engineering. It is rarely a single, fixed set of three concepts applicable everywhere; rather, it is a grouping of three that serves the most immediate purpose of the measurement task at hand.
When considering the bedrock of scientific inquiry, the focus narrows to the fundamental units from which all other measurable quantities can be derived. In the realm of physics, this often boils down to the triad of length, mass, and time. These three are considered fundamental because they cannot be easily defined in terms of other basic measurements; they are the starting points for constructing the language of physical laws. If you consider the International System of Units (SI), which serves as the modern standard globally, these three concepts are clearly represented by the meter (length), the kilogram (mass), and the second (time).
# Physical Basis
The meter, the SI unit for length or distance, defines how far apart two points in space are. It is the cornerstone of spatial measurement, essential for everything from calculating the distance to a star to determining the size of a molecule. Historically, definitions have evolved to become more precise; today, the meter is defined by the distance light travels in a vacuum during a specific, incredibly short interval of time.
Next is mass, represented by the kilogram. Mass quantifies the amount of matter contained within an object, which is distinct from weight, although in common parlance, the terms are often used interchangeably. Weight is technically a force (mass times gravity), whereas mass is an intrinsic property. The kilogram has seen recent redefinition, now being fundamentally linked to Planck's constant, further solidifying its place as a universal constant rather than an object-dependent standard.
Finally, there is time, measured in seconds. Time describes the progression of events, one after the other. Like the meter, the modern definition of the second is rooted in atomic physics, relying on the frequency of radiation associated with a specific transition in the cesium-133 atom. This atomic precision ensures that a second measured in one laboratory is identical to one measured anywhere else, a requirement for a truly fundamental unit.
If we look at these three—length, mass, and time—as the core components of mechanics, they explain motion, force, and energy, making them arguably the "three main measurements" in classical science.
# Spatial Dimensions
A different, yet equally valid interpretation of "three main measurements" arises when describing the extent of a physical object or space itself. In this geometric and descriptive context, the primary trio consists of length, width, and height. These are often referred to as the three spatial dimensions.
Length and width define the extent across a surface, while height provides the vertical dimension, completing the description of volume. Consider measuring a shipping container: you need its length, its width (or breadth), and its height to ensure it fits onto a truck or ship. These three measurements are essential for calculating surface area and, when all three are multiplied, determining volume.
There is an overlap here with the physical foundation. The geometric length is conceptually the same as the physical unit of length (the meter). However, width and height are essentially just different orientations of length in a Cartesian coordinate system. Width could be considered length measured along the y-axis, and height along the z-axis, with the primary length along the x-axis. This highlights an important distinction: in physics, length, mass, and time are qualitatively different types of measurement (different dimensions), while in geometry, length, width, and height are quantitatively the same type (all are measures of distance) but oriented differently in space.
When you are designing something, like an architectural blueprint or a 3D model, you are dealing almost exclusively with these three spatial dimensions. The measurement of mass or time rarely enters the initial design phase unless structural loads (mass) or construction scheduling (time) are immediately factored in.
# Systemic Structure
While length, mass, and time are often cited as the core three, it is important to recognize that the modern system of measurement, the SI, actually rests on seven base units. If we are talking about the system itself, all seven are equally fundamental to their respective domains. The other four base units include:
- Electric Current: Measured in Amperes (A).
- Thermodynamic Temperature: Measured in Kelvins (K).
- Amount of Substance: Measured in Moles (mol).
- Luminous Intensity: Measured in Candelas (cd).
The vast majority of everyday measurements, however, are derived units, built from these base units. For instance, speed is derived from length divided by time (), and density is derived from mass divided by volume ().
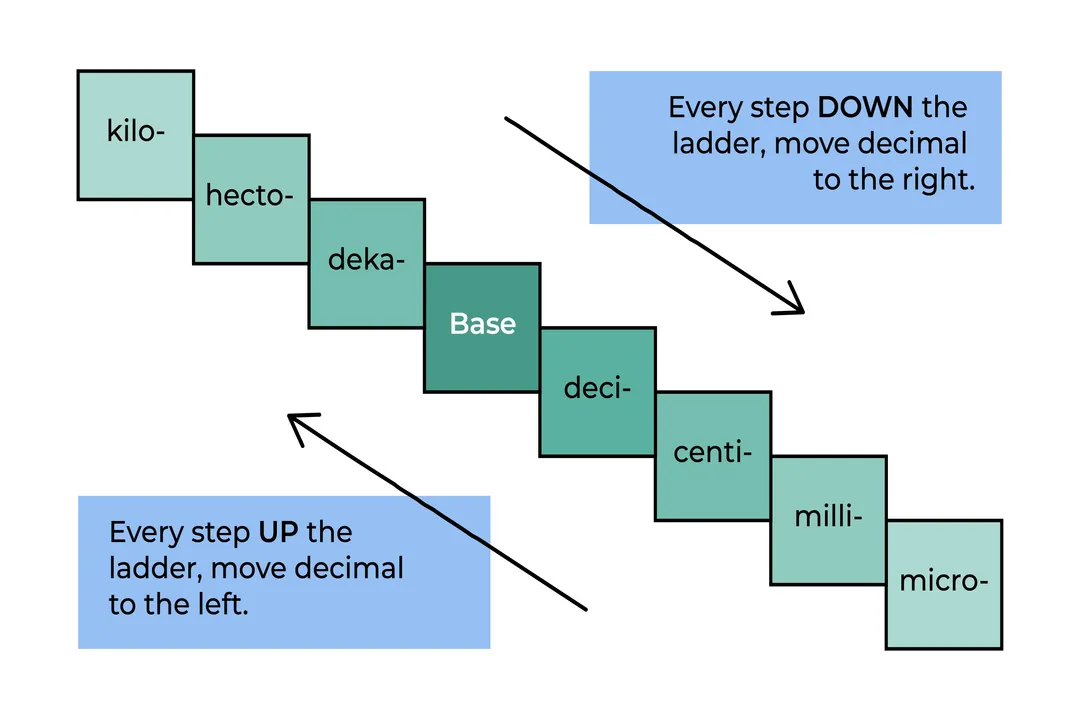
The structure of the metric system, or SI, is characterized by its coherence and the use of powers of ten, which simplifies calculations immensely compared to older systems. For example, when moving from millimeters to meters, you divide by 1,000. This base-ten structure is a major advantage for scientists and engineers globally. A common sticking point for those learning measurement is correctly applying the prefixes (kilo, centi, milli), which define the magnitude difference between units of the same dimension—be it length, mass, or time. Understanding that and shows how the concept of the unit is shared across dimensions.
To truly appreciate the power of the SI system, consider this: if you were tasked with measuring the volume of a swimming pool, you would measure its length, width, and depth (all length dimensions) and multiply them. If you were measuring the mass of the water inside, you would use the kilogram. If you were tracking how long it takes to fill, you'd use seconds. The relationship between these derived quantities, such as the density of water, remains constant whether you measure in SI units or, say, U.S. Customary units, but the calculation is significantly cleaner in the metric format.
# Applied Contexts
Beyond pure physics and geometry, different professional fields emphasize different measurements as "main" for their daily operations. In fields like nursing or pharmacy, where precision directly impacts patient safety, the critical triad often shifts to reflect what needs to be administered or monitored: length (or height), weight (mass), and volume (or time).
While length and weight (mass) carry over from the fundamental set, volume often replaces the more abstract concept of time as the third key measurement in dosage calculations. Measuring liquid medication requires volume (often in milliliters or liters), which is a derived unit based on length cubed (). Time remains critical for monitoring infusion rates or the intervals between doses, creating a practical measurement trinity for clinical care.
Consider a clinical scenario: a physician orders a drug dosage based on the patient's weight (mass). The nurse needs to measure the precise volume of the liquid drug to administer. The infusion pump needs to be set to deliver that volume over a specific time interval. Here, weight, volume, and time are the operational "three main measurements," even though mathematically, volume is derived from length.
# Consistency and Dimensional Analysis
The key takeaway across all these interpretations—whether it's or —is the importance of dimensional consistency. A major pitfall in any quantitative work is mixing units improperly. You cannot meaningfully add a length measurement (like 5 meters) to a mass measurement (like 10 kilograms), nor can you subtract a time measurement from a length measurement. This concept is known as dimensional analysis, a technique vital in physics and engineering to check calculations.
For instance, if you are calculating the average speed of a car, you divide total distance (length) by total time. If someone reports the distance as 100 kilometers but the time as 90 minutes, you cannot simply divide . You must first convert one unit to match the other’s required dimension. The standard SI approach would be to convert 90 minutes into hours (1.5 hours) to yield a result in kilometers per hour (). If you used a non-standard combination, like meters per minute, the resulting number would be mathematically correct but meaningless in standard scientific communication.
Here is a quick reference table showing how the three dominant interpretations map onto the SI base units:
| Context | Measurement 1 | Measurement 2 | Measurement 3 | Type of Dimension |
|---|---|---|---|---|
| Physics Foundation | Length | Mass | Time | Fundamental/Base |
| Spatial Description | Length | Width | Height | Derived (all distance) |
| Clinical Application | Mass (Weight) | Volume | Time | Mixed (Base & Derived) |
| SI Base Units | Meter (m) | Kilogram (kg) | Second (s) | Base Units |
An interesting practical point arises when moving between systems, such as the U.S. Customary System (often using feet, pounds, seconds) and the SI metric system. While the concepts are the same (distance, mass, time), the ratios between them are arbitrary constants derived from historical convention rather than powers of ten. For example, converting pounds to kilograms requires multiplying by approximately $0.453592$. This constant factor is a direct consequence of not sharing a unified base definition, unlike the metric system. When attempting to perform advanced calculations, ignoring the need to convert between these two systems in a single equation is a prime source of error, far more common than miscalculating a metric prefix. This is why, in any technical field aiming for international collaboration, the SI triad of meter, kilogram, and second forms the non-negotiable standard basis.
Ultimately, while length, mass, and time are the fundamental building blocks recognized by science, and length, width, and height define the space we inhabit, the "three main measurements" you need to focus on at any given moment are dictated by the question you are trying to answer. For construction, it’s ; for chemistry, it might be ; and for fundamental physics, it remains the foundational triplet: length, mass, and time.
#Videos
Math Antics - Intro to the Metric System - YouTube
Related Questions
#Citations
What are the three basic units of measurement? - Quora
Metric system - Wikipedia
What does three measurements mean? : r/ADO - Reddit
Measurements - Math: Basic Tutorials - The Learning Portal
System of Measurements | Types | Conversion Units | Examples
What are the three metric units of length? - Answers
Metric System Basics | Mathematics for the Liberal Arts
What are the three fundamental units of measurement in physics?
Length, Width & Height | How to Read Dimensions - Smartick
Math Antics - Intro to the Metric System - YouTube

