What defines a reference frame?
The concept of a reference frame anchors our understanding of the physical world, providing the necessary stage upon which all motion, position, and interaction can be described. It is, at its most fundamental level, simply a coordinate system plus a clock. [1][4] Without one, statements about where something is or how fast it is moving are meaningless noise; they lack context. [2][6] Imagine trying to describe a car crash without agreeing on whether you are observing it from the sidewalk, from another car traveling alongside, or from a traffic camera mounted high above—the measured velocities and impacts will differ wildly depending on your chosen viewpoint. [3][7] This dependence on the observer is the defining characteristic of the reference frame.
A reference frame allows an observer to measure the position of an object relative to a chosen origin point within that system. [2] To fully describe the state of an object, you need not just its position relative to the frame’s origin, but also its velocity and acceleration—all measured using the same frame’s coordinate axes and the same clock. [6] The collection of all points in space from which an observer measures physical events constitutes that observer's reference frame. [8]
# Relative Motion
The critical realization in classical mechanics, one often credited to Galileo, is that motion is relative. [8] There is no absolute, universal rest state against which all motion can be judged. [9] If you are sitting on a perfectly smooth train with the shades drawn, moving at a constant velocity, you cannot perform any internal experiment—dropping a ball, tossing a coin—that would tell you whether the train is moving or perfectly stationary. [8] The laws of physics, crucially, remain the same for all observers moving at constant velocity relative to one another. [1][8] This principle of relativity is what makes the choice of frame so powerful: it simplifies the description of motion by allowing us to choose the frame that makes the mathematics easiest. [3]
Consider a scenario where a passenger on that train tosses a ball straight up. From the passenger’s perspective (their reference frame), the ball goes up and comes straight back down to their hand. [6] Now, consider a friend standing stationary on the ground watching the train pass. To this friend, the ball does not just move vertically; it moves both vertically and horizontally along with the train. [7] The friend sees the ball trace an arc. Both descriptions are perfectly valid descriptions of the same physical event, just anchored to different origins and coordinate systems. [1][2] The difference in the perceived path highlights how the frame dictates the description of the motion. [6]
This relativity extends to the mathematical description of how observers translate measurements between their frames. For frames moving at constant, non-relativistic speeds, the transformation equations—known as the Galilean transformations—are straightforward additions and subtractions of velocities. [1] However, as speeds approach the speed of light, this simple addition breaks down, requiring the more complex Lorentz transformations inherent to Einstein's Special Relativity. [1][9] This necessity for different transformation rules underscores that the definition of the frame is intrinsically linked to the underlying structure of spacetime itself. [9]
# Inertial Systems

While any coordinate system coupled with a clock can define a reference frame, physics often requires a special subset: inertial reference frames. [1][2] An inertial frame is one that is either at rest or moving at a constant velocity. [1] The defining characteristic of an inertial frame is that Newton's first law of motion—the law of inertia—holds true within it. [1] In an inertial frame, an object subjected to no net external force moves at a constant velocity (which includes remaining at rest). [1][8]
Contrast this with a non-inertial reference frame, which is any frame that is accelerating—meaning it is speeding up, slowing down, or rotating. [1] If you are in a car that suddenly brakes hard, you lurch forward, even though no physical object directly pushed you forward in the absolute sense. [4] In the car’s non-inertial frame, it feels like a mysterious force—an inertial force or fictitious force—pushed you. [1] Examples include the centrifugal force felt on a merry-go-round or the Coriolis effect influencing weather patterns. [1] For physicists, non-inertial frames are more complex because describing motion requires introducing these non-physical, fictitious forces to make Newton's second law () appear to work within that accelerating system. [1]
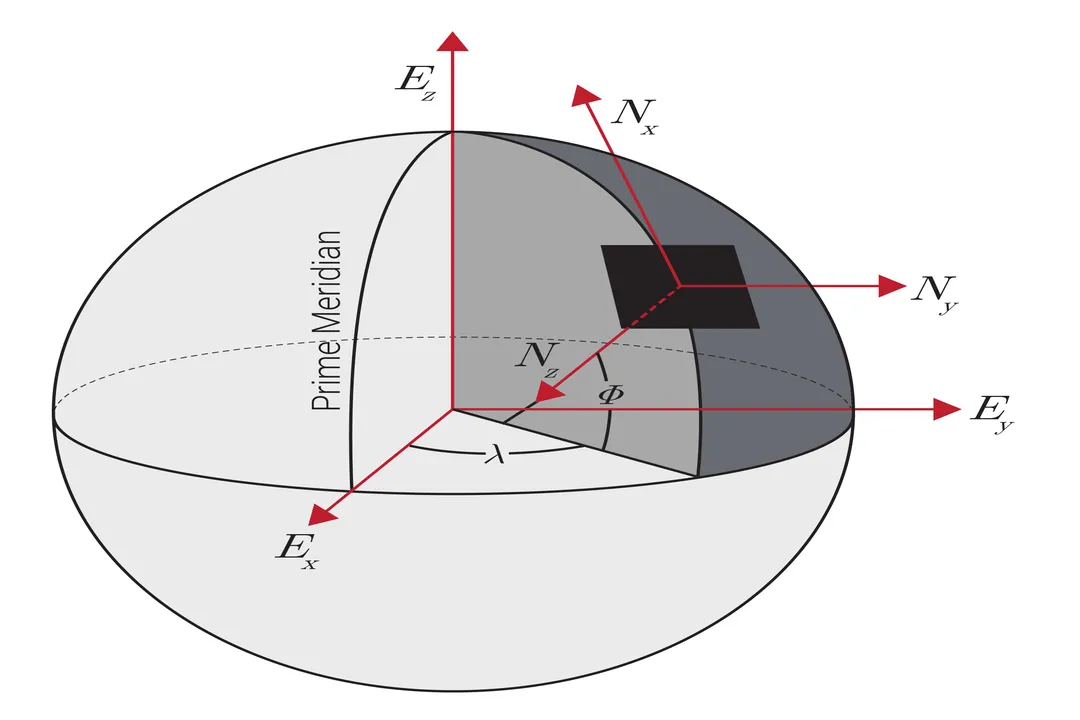
For many engineering and navigational tasks, the distinction is critical. When designing a drone navigation system, for instance, the designer must choose a fixed, external reference frame (like the Earth's surface, perhaps simplified as an Earth-Centered, Earth-Fixed or ECEF frame) to define absolute position and velocity. [4] The drone's own internal sensors measure motion relative to its body (a moving, accelerating, non-inertial frame). The entire navigation algorithm is dedicated to accurately translating the body frame's relative acceleration measurements into meaningful velocity and position changes within the global frame using coordinate transformations. [4] If the required accuracy is high, the math must account for the Earth's rotation and curvature, subtly shifting the operational definition of what constitutes an "inertial" approximation for that scale. [4]
# Defining Coordinates
A reference frame is not just an abstract point of view; it requires concrete mathematical structure. [4] This structure is established by defining the axes and the zero point of measurement. [2]
For a basic one-dimensional problem, like movement along a straight track, the frame needs only one axis and an origin point. [6] A position might be described simply as meters. [2]
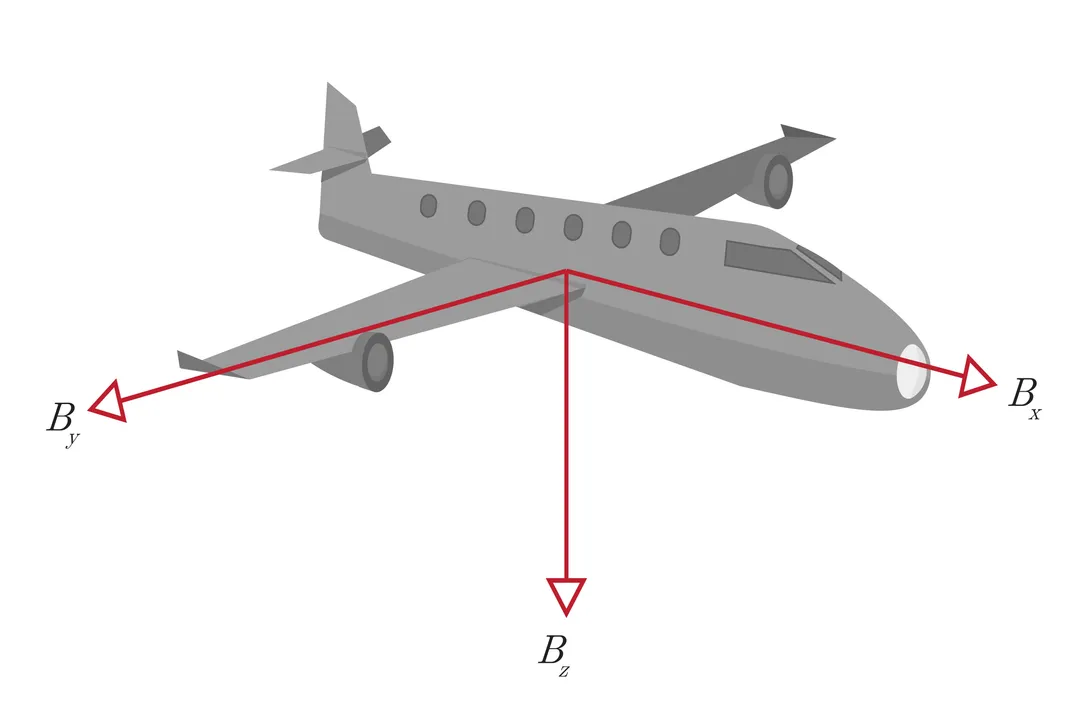
For movement in three dimensions, like an airplane in the sky, the frame requires a set of three mutually perpendicular axes (, , and ) that intersect at the origin. [4] Every point in space is then uniquely located by three coordinates . [1] The orientation of these axes relative to some known fixed direction—like true North or the plane of the Earth’s equator—is what distinguishes one specific coordinate system from another, even if they share the same origin. [4]
A helpful way to visualize this complexity is to compare the simplest and most complex frames a general physicist or engineer might use:
| Frame Type | Axes Required | Primary Motion Type | Key Transformation Math |
|---|---|---|---|
| 1D Slider | 1 (e.g., ) | Linear translation | Simple addition/subtraction |
| Standard 3D Lab | 3 Cartesian () | Translation and Rotation | Coordinate rotation matrices |
| Earth-Fixed (ECEF) | 3 Cartesian (aligned to Earth) | Earth rotation, local motion | Requires accounting for Earth's angular velocity |
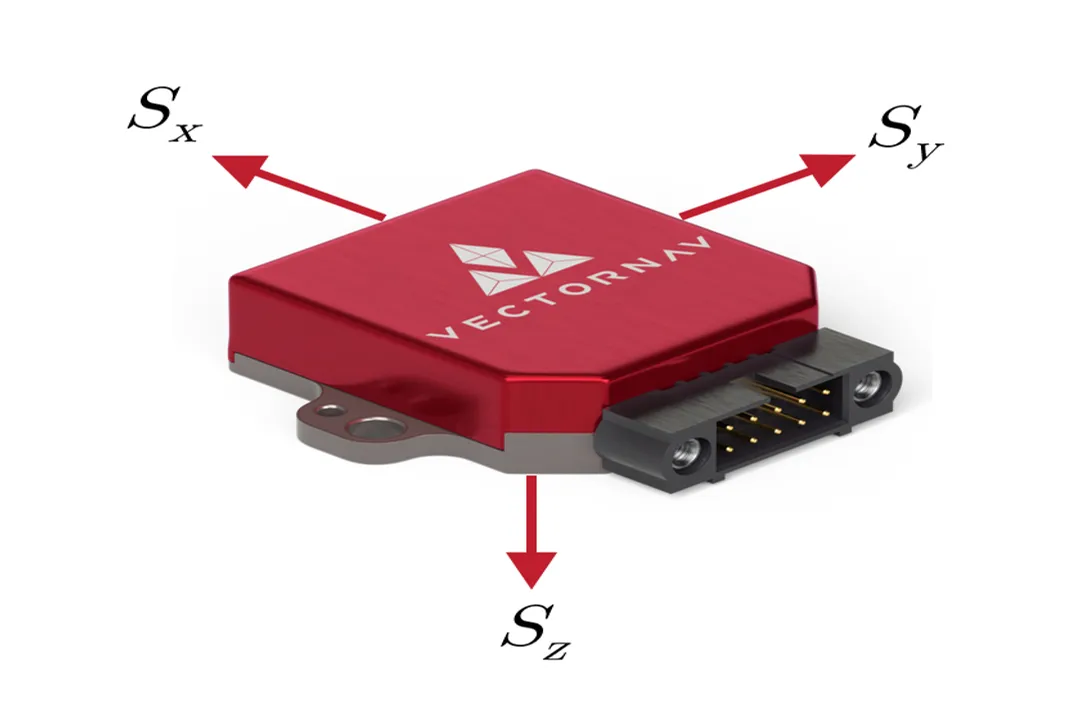
| Spacecraft Body Frame | 3 (aligned to craft structure) | Highly accelerating, rotating | Output of Inertial Measurement Units (IMUs) [4] |
The mathematical process of relating coordinates between two different frames—say, translating measurements from the accelerating body frame of a rocket to a fixed inertial frame near the Earth—is managed through coordinate transformations. [1][4] These transformations ensure that when one observer reports a position, another observer in a different frame can calculate the exact position as they see it, preserving the underlying physical laws. [1][4]
# Biological Frames
The necessity of reference frames extends well beyond inanimate objects and classical mechanics; our own bodies operate on complex systems of internal reference frames to control movement and perception. [5] When you reach out to grab a cup of coffee, your brain is continuously solving a complex reference frame transformation problem. [5]
Your eyes provide visual information relative to your retina (a sensorimotor frame). [5] Your inner ear provides data on head acceleration and orientation relative to gravity (a vestibular frame). [5] Your arm and hand position are described relative to your shoulder or torso (a body frame). [5] To successfully execute the reach, the brain must align these different internal frames, calculating the required motor commands to move the hand's position in the world frame (the frame where the coffee cup resides). [5]
The brain doesn't just use one static system; it dynamically switches between reference frames depending on the task. [5] For example, when you are standing still, your brain might heavily weight the vestibular frame to maintain balance relative to the Earth's gravity. If you start walking, the body frame takes precedence as you coordinate limb movements relative to your torso's current motion. [5] A fascinating aspect of this neurological processing is how it handles transformations—the brain must map changes measured in one frame (like eye movement) onto an action in another frame (like moving the arm). [5] Failures in these transformations, perhaps due to conflict between sensory inputs (like visual motion sickness), clearly demonstrate how essential the consistent application of the correct frame is to coherent action. [5]
# Context and Transformation
Historically, the concept evolved from a simple navigational tool into a cornerstone of modern physics. [8] Before the understanding of relativity, the prevailing view, often associated with Newtonian mechanics, presumed the existence of an absolute, fixed reference frame—an "aether"—against which all motion could be measured. [9] Galileo, however, provided the early framework showing that only relative motion mattered for mechanics within mechanical systems. [8]
The modern scientific understanding solidifies this relativity while also revealing deeper structural connections between space and time. [9] Einstein’s theories showed that the transformations between inertial frames depend on the speed of light being constant for all observers, leading to effects like time dilation and length contraction when using the Lorentz transformations. [1]
The key takeaway remains that a reference frame is a conceptual tool defined by its relationship to what is being measured. [2] It is the conscious decision to set the origin, choose the orientation of the axes, and synchronize the clock that defines the mathematical structure. [4] This initial choice is what dictates the resulting description of any subsequent event, proving that in physics, where you stand mentally is as important as what you are observing. [1][3] If we needed to model a system where an object always moved in a straight line according to Newton's laws, we would be forced to work backward from that constraint to define the only possible inertial reference frame for that object. [1]
#Videos
What are frames of reference in physics? - YouTube
Reference Frames - YouTube
Related Questions
#Citations
Frame of reference - Wikipedia
Frames of Reference — Isaac Science
What are frames of reference in physics? - YouTube
Reference frames and how they are used in inertial navigation
Reference Frames and Coordinate Transformations
Introduction to reference frames (video) - Khan Academy
Reference Frames - YouTube
Frames of Reference and Newton's Laws - Galileo
Space and Time: Inertial Frames

