What defines harmonic overtones?
The sound an instrument produces is rarely a single, pure frequency. When a violin string vibrates, or when a vocalist sings a note, the resulting wave reaching our ears is actually a combination of several distinct frequencies happening all at once. [4][5] These constituent frequencies, which exist above the lowest, most dominant frequency heard, are generally known as overtones. [5][6][7] The lowest of these audible frequencies is called the fundamental, the note you identify as the pitch (e.g., Middle C). [6][8] Everything else vibrating above that foundation contributes to the final character of the sound. [1][5]
The definition of an overtone hinges on its relationship to that fundamental tone, and that relationship is categorized mathematically. If you are listening to a sound where all the accompanying frequencies are exact integer multiples of the fundamental, you are experiencing a set of harmonics. [1][5][6] This specific mathematical relationship is what gives musical instruments their characteristic, pleasing sound. [3]
# Partial Frequencies
In the physics of sound, any frequency component of a complex tone is often referred to as a partial. [5] This is a neutral term, covering all frequencies present besides the fundamental. [6] An overtone, by precise definition, is any partial that has a frequency higher than the fundamental frequency. [1][7]
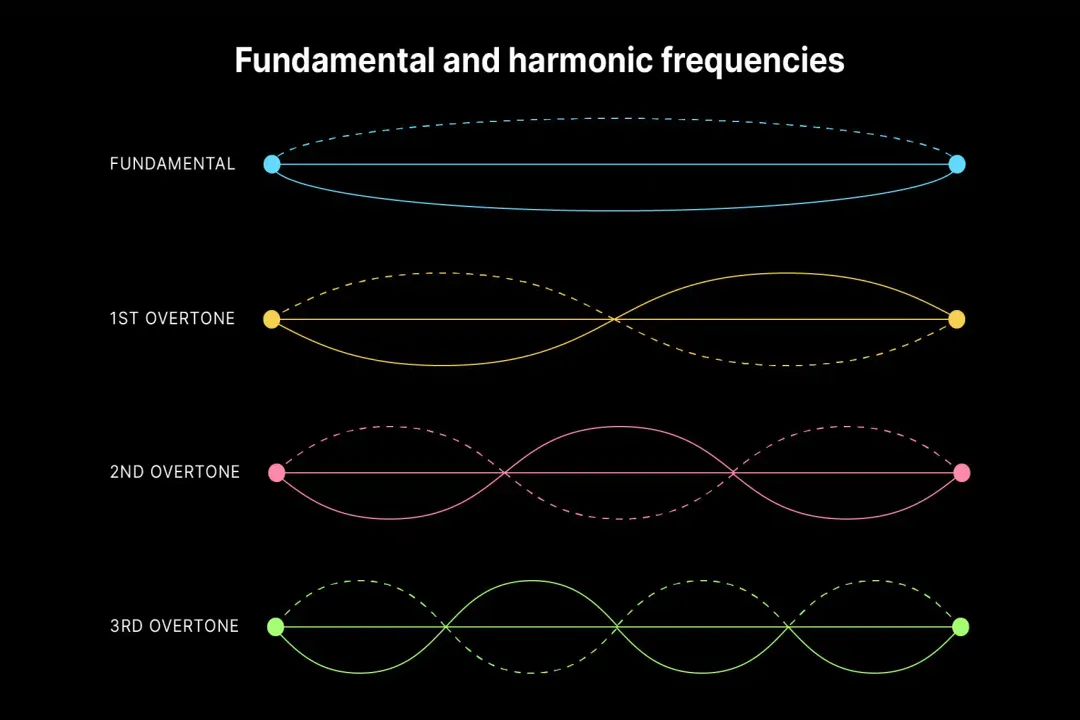
Consider a string vibrating. It doesn't just vibrate along its entire length; it also vibrates in segments—halves, thirds, quarters, and so on. [5] Each of these distinct ways the string vibrates produces a corresponding frequency. [5] The lowest frequency produced by the entire length vibrating as one unit is the fundamental, or first harmonic. [6][8] All other frequencies created by these smaller, segmented vibrations are the overtones. [1]
It is vital to distinguish between the general concept of an overtone and the specific, mathematically defined set known as harmonics. If a tone possesses only harmonics, then its first overtone is its second harmonic (twice the fundamental frequency), its second overtone is its third harmonic (three times the fundamental frequency), and so forth. [6] However, some sounds, particularly those from bells, some percussion instruments, or those produced by striking an object rather than sustaining a vibration, contain partials that do not fit this neat integer relationship. [1] These non-integer partials are called inharmonic overtones. [1][5] Therefore, the rule of thumb is straightforward: every harmonic is an overtone, but not every overtone is a harmonic. [1][5][7]
# Harmonic Relationship
The defining characteristic of a harmonic overtone is its precise mathematical spacing relative to the fundamental frequency (). [3][4] If is the fundamental frequency, the harmonics are , , , and so on, where the multiplier () is a positive integer. [3][8] This constant, integer-based progression creates a predictable and consonant structure in the sound wave. [3]
Let’s illustrate this relationship with a common tuning reference, A4, which vibrates at . [3]
| Harmonic Number () | Frequency Calculation | Resulting Frequency (Hz) | Overtone Rank |
|---|---|---|---|
| 1 | $440$ | Fundamental | |
| 2 | $880$ | 1st Overtone | |
| 3 | $1320$ | 2nd Overtone | |
| 4 | $1760$ | 3rd Overtone | |
| 5 | $2200$ | 4th Overtone | |
| 6 | $2640$ | 5th Overtone | |
| [3][4] |
This predictable doubling and tripling of the base frequency creates the backbone of Western music theory, as the intervals formed by these first few harmonics—the octave (2:1 ratio), the perfect fifth (3:2 ratio), and the perfect fourth (4:3 ratio)—are foundational to consonance. [3][6] When analyzing the sound spectrum of a tuned instrument, these energy peaks align perfectly on this grid, confirming their harmonic nature. [8]
# Series Mathematics
The concept of the harmonic series is deeply tied to the physics of vibrating strings, air columns in pipes, and even the vocal cords. [5] It describes the sequence of frequencies a perfectly vibrating, one-dimensional system will naturally produce. [3][4] While idealized, this model explains why certain sounds are perceived as musically "pure" or "clear". [7]
The physical mechanism behind this involves standing waves. A string fixed at both ends can only support vibrations where the ends remain stationary (nodes). [5] The longest possible standing wave fills the entire length, setting the fundamental frequency. The next possible standing wave fits two antinodes separated by a node, dividing the string into two equal vibrating sections, which produces a frequency exactly double the fundamental (the octave). [5] This division pattern continues mathematically into thirds, quarters, fifths, and beyond. [3][4]
It is worth noting a subtle difference in terminology often found in acoustics versus musical composition. In acoustics, the first frequency is , and the subsequent frequencies are , etc., where . [6] In musical contexts, however, is usually called the first harmonic, the second harmonic, and so on, which simplifies the overtone indexing discussed earlier. [6] This dual numbering system can sometimes cause confusion when reading different technical sources, but the underlying physical reality—the integer multiples—remains the same. [8]
# Tone Quality
If all instruments produced only the fundamental frequency, every flute, piano, or human voice would sound exactly the same, regardless of the instrument—there would be no timbre. [6][7] Timbre, or tone quality, is what allows us to distinguish a trumpet from a cello playing the exact same note at the same volume. [1][5] This distinction is entirely dependent on the relative strength (amplitude) of the overtones present in that specific sound. [1][7]
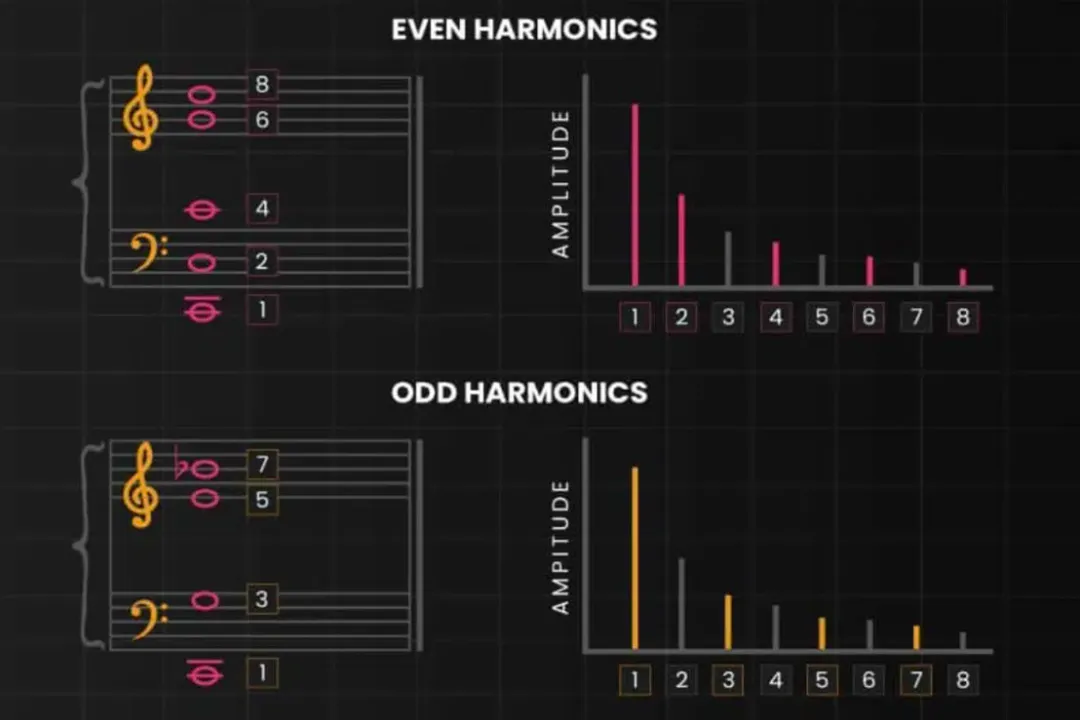
The spectrum of frequencies present in a sound, along with their respective intensities, forms the spectral envelope of that sound. [7] For instance, a clarinet tends to emphasize the odd-numbered harmonics (), often resulting in a hollower or reedier tone compared to a violin, which strongly emphasizes the lower harmonics (). [7] If you are working in audio production and trying to change the perceived character of a synthesized sound, you are often adjusting the sliders that control the volume of individual harmonics. [7] A slight boost to the 7th or 9th overtone in a synthesized waveform can introduce a metallic quality not present in the original sound, demonstrating how these higher partials shape perception. [1]
This variability is even more pronounced when we encounter inharmonic partials. Consider a piano's middle C versus a cymbal crash. The piano note is structured around a clear harmonic series, making the pitch stable and identifiable. [8] The cymbal crash, conversely, contains many partials that are not integer multiples of the fundamental, which is why a cymbal doesn't really have a "note" you can easily sing; its sound is defined by noisy, inharmonic energy across the spectrum. [1][5] The lack of a stable, predictable relationship between the partials causes our ear to interpret the sound as noise or clang rather than a defined musical pitch. [1]
# Auditory Perception
While the physics dictates the mathematical ratios, the human ear and brain interpret these complex vibrations. [7] Our auditory system is remarkably adept at picking out the fundamental frequency, even if that fundamental frequency is physically absent from the sound wave itself—a phenomenon known as the missing fundamental. [8] This demonstrates that the brain reconstructs the pitch based on the relationships between the overtones, not just the presence of the lowest frequency. [8] If you filter out the component from a rich and combination, the listener will likely still perceive the pitch as because their brain recognizes the $2:3$ ratio between those higher partials. [8]
When designing instruments or editing audio, understanding this perceptual dependency is key. For example, in instrument making, a luthier might intentionally shape the body of a guitar to slightly dampen a specific inharmonic overtone that is causing a distracting "buzz" at a certain dynamic level. [7] This is a practical application of spectral control—identifying an unwanted partial that muddies the sound and reducing its energy without disrupting the desired harmonic structure. [1] If an engineer removes a specific frequency content from a recording, they must be careful; removing a low-numbered harmonic (like the 4th harmonic) will shift the perceived timbre significantly, whereas removing a very high, faint overtone might be inaudible or only marginally affect the warmth of the sound. [7] The prominence of higher overtones generally contributes to the brightness or brilliance of a sound, while the dominance of lower overtones contributes to depth and fullness. [5]
# Tuning Systems
The historical development of musical tuning systems is, in many ways, an attempt to tame the mathematical wildness of the harmonic series and fit its pure ratios onto an instrument with fixed divisions, like a keyboard. [3] The pure intervals derived from the series are mathematically clean—a perfect fifth is exactly the frequency of the fundamental. However, stacking many of these perfect ratios together (like tuning 12 fifths in a row) does not perfectly lead back to the starting pitch multiplied by a power of two (an octave). [3] This discrepancy, known as comma, is why modern equal temperament tuning slightly adjusts every interval, making them slightly inharmonic by the strict standards of the natural harmonic series, yet allowing modulation across all keys. [3][6] This trade-off—sacrificing the purity of individual intervals for overall flexibility—is central to understanding why sounds sometimes sound slightly "off" on a piano versus a perfectly tuned string instrument played fretless. [8] The pure harmonic system is the ideal from physics, while equal temperament is the practical compromise for music performance. [3]
#Videos
Music Theory | What is the Overtone Series? - YouTube
Related Questions
#Citations
Overtone - Wikipedia
Harmonic Overtones - DPA Microphones
Overtones and Harmonics - HyperPhysics Concepts
Overtone Series (aka Harmonic Series) in Music | muted.io
Sound - Overtones, Frequency, Wavelength | Britannica
What Is the Overtone Series & How Do Overtones Work?
Harmonics and Overtones 101: Sculpt Sound like a True Expert
Music Theory | What is the Overtone Series? - YouTube
What are overtones? - Music: Practice & Theory Stack Exchange

