How does population growth become exponential?
The idea that a population can explode in size, seemingly without limit, hinges on a specific mathematical relationship: exponential growth. This pattern is characterized by a growth rate that is proportional to the current population size, meaning the larger the group gets, the faster it multiplies. [2] It's not just about adding a fixed number of individuals each year; it's about a fixed percentage increase applied to an ever-increasing base. In the context of populations—be they bacteria, invasive species, or the human race—this process leads to an accelerating rate of increase, often visualized as a steep, upward-curving line on a graph. [1][2]
# Growth Definition
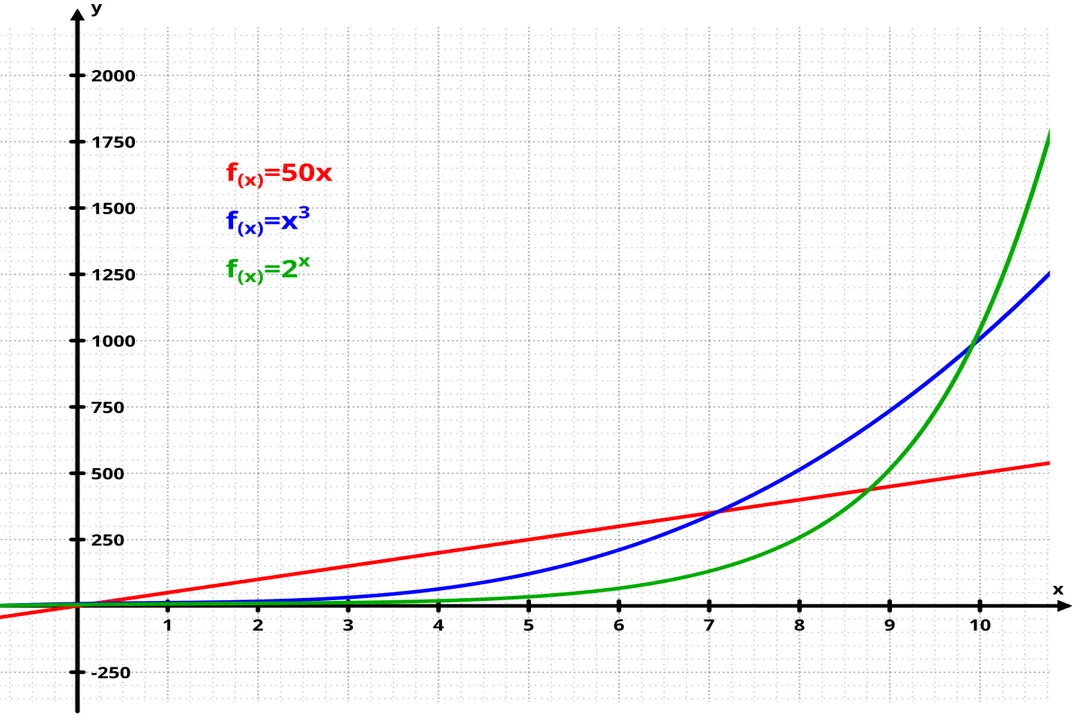
At its heart, exponential growth describes a situation where the rate of change over time is directly related to the current amount. [2] Imagine a population where every individual reproduces at a constant rate, say, doubling every hour. In the first hour, one individual becomes two. In the second hour, those two become four. The third hour yields eight, then sixteen, thirty-two, and so on. [2] The actual number added in each time interval increases significantly, even though the rate of reproduction (the doubling time) stays the same. [1] This mathematical process is captured by the equation , where is the population size, is time, and is the intrinsic rate of increase, often called the per capita growth rate. [1][6] For a population to exhibit true exponential growth, two primary conditions must be met: the growth rate () must be constant, and the population must have unlimited access to resources. [6]
# J Curve Shape
When ecologists plot this kind of growth over time, the resulting graph forms a characteristic J-shaped curve. [1][3][6] This curve is synonymous with the pattern of exponential population increase. [6] It starts slowly, mirroring the relatively small initial numbers, but then curves sharply upward as the large numbers begin to multiply rapidly. [1] This phase of growth is often seen when a species colonizes a new environment with abundant resources and few predators, or when a population recovers quickly after a mass die-off, assuming the environment can temporarily support the rapid influx. [3] The initial slow increase is deceiving; it masks the massive potential for rapid growth that is inherent in the geometric nature of the multiplication process. [2]
In the real world, especially in ecology, this pure exponential phase is rarely sustained indefinitely. It represents a theoretical maximum growth rate under ideal conditions. [6] If a population were truly to follow this curve forever, it would quickly become unsustainable, leading to an eventual crash or a shift in the growth pattern. [1][3]
# Human History
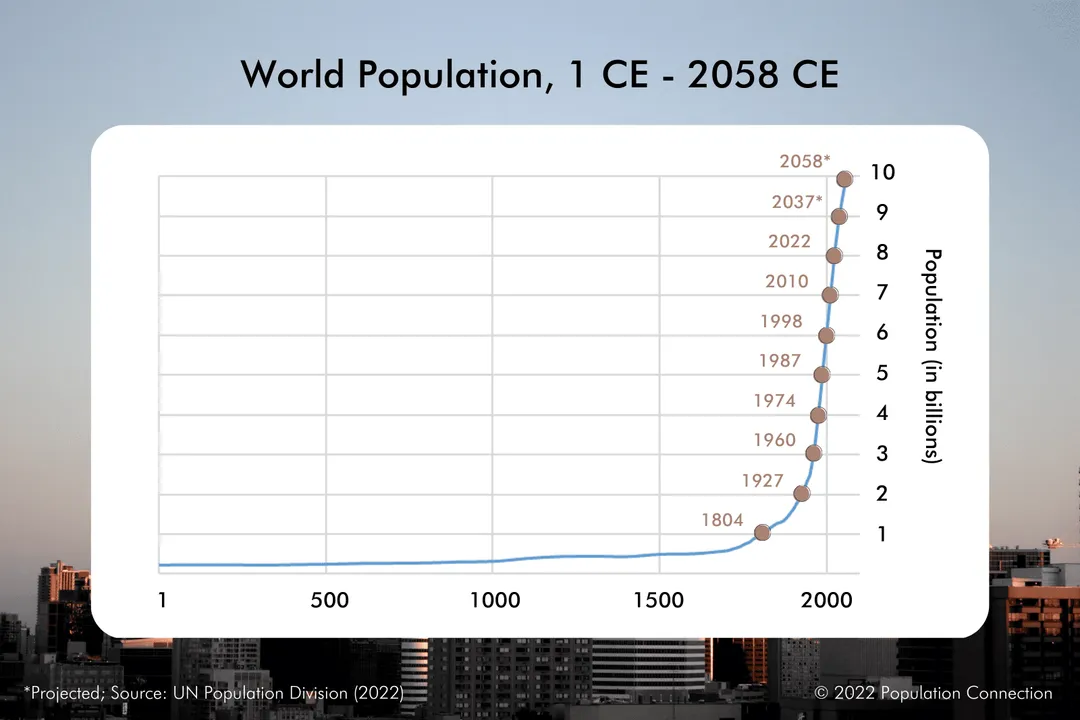
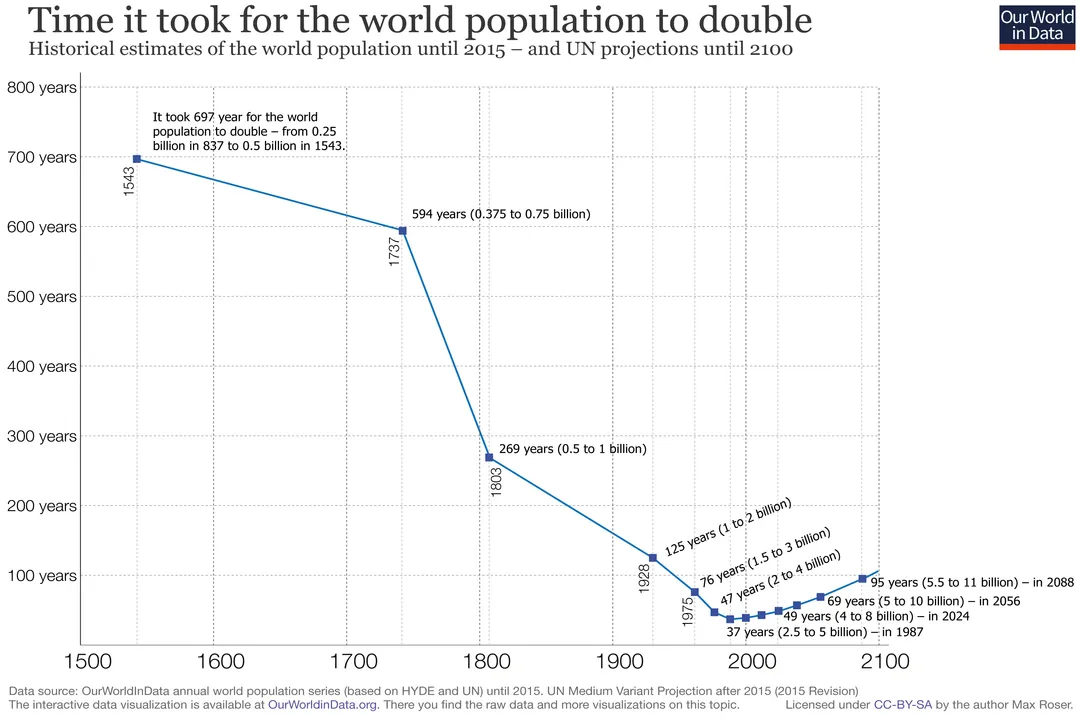
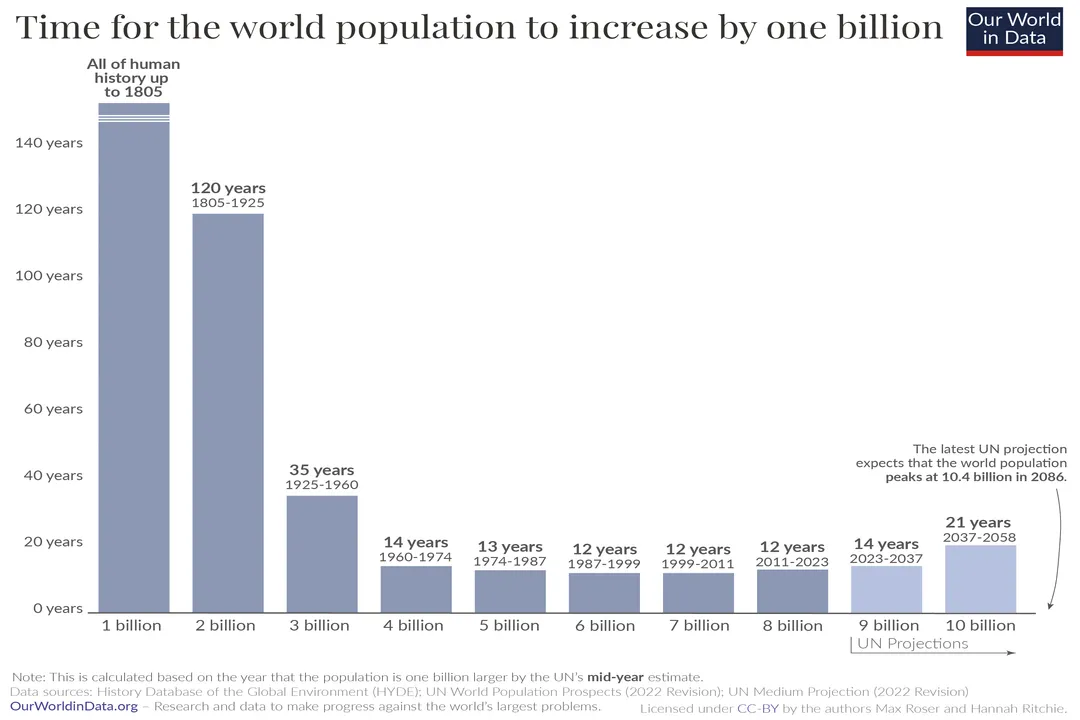
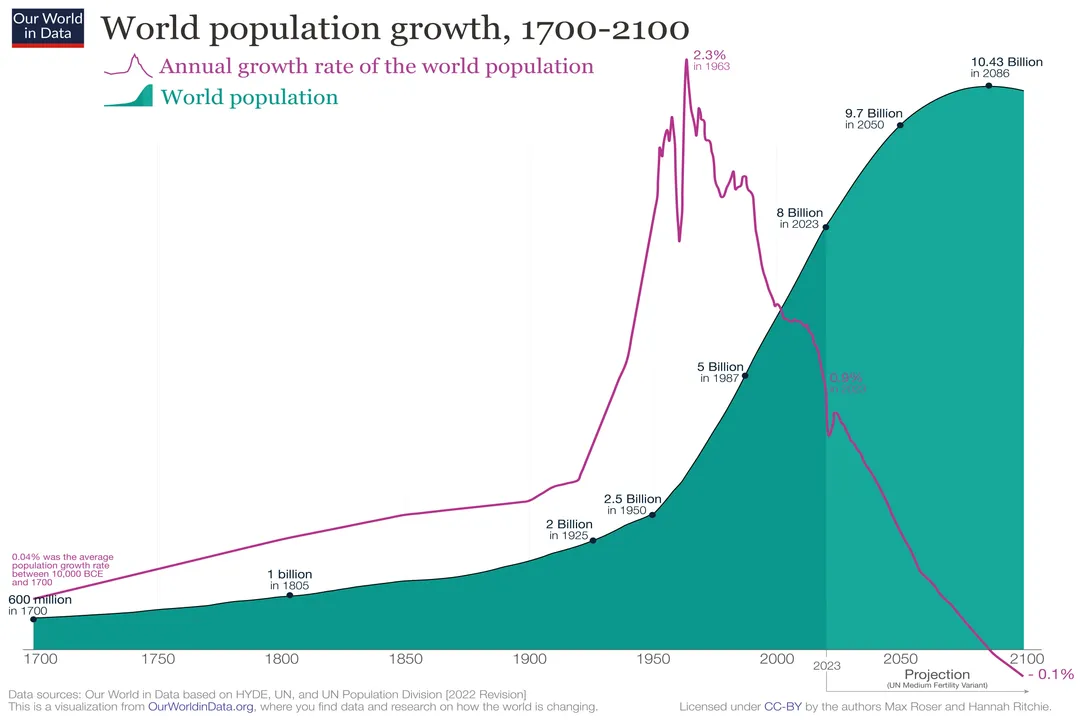
The story of the human population mirrors this concept over millennia, though the actual growth has been far from a smooth curve; it's marked by long plateaus and sudden, dramatic accelerations. [8] For most of human history, population growth was incredibly slow, often hovering near zero or experiencing minor fluctuations due to famine, disease, or conflict. [4] For instance, it took until about 1800 AD for the global human population to reach one billion people. [8] This initial, slow climb represents a very low effective growth rate over millennia. [4]
What changed to push humanity onto an exponential-like trajectory? The acceleration began in earnest with the Industrial Revolution and advancements in medicine and sanitation. [4] Suddenly, the death rate plummeted across wide swaths of the globe, while birth rates often remained high for a time. [4] The global population took only about 123 years to jump from one billion to two billion, reaching that mark around 1927. [8] This is a stark illustration of compounding effect. The next billion took even less time—just 33 years, reaching three billion around 1960. [8] This rapid tightening of the doubling time is the hallmark of exponential acceleration in a real-world context. A local town council might see its population increase by 50 people in a year and consider that significant, but if the starting population was 1,000, that's a 5% growth rate. If that 5% rate persists over fifty years, the town grows from 1,000 to over 11,400, demonstrating how a seemingly modest rate compounds into massive numerical change over time. [2]
# Limiting Factors
The reason pure exponential growth cannot continue indefinitely in any closed system, whether a petri dish or the Earth, is the introduction of limiting factors. [3][6] In ecological terms, this means the population eventually exceeds the environment's carrying capacity (). [3][6] Carrying capacity is the maximum population size that a particular environment can sustain indefinitely, given the available resources like food, water, space, and light, and the environment's ability to absorb waste. [3][6]
When resources become scarce, the per capita growth rate () begins to decline because death rates rise or birth rates fall, or both. [1] This slowdown signals a transition away from the idealized J-curve and toward a more realistic model: the logistic growth curve. [1][3] The logistic model results in an S-shaped curve, where growth initially mirrors the exponential phase but then levels off as it approaches the carrying capacity (). [1][3] The transition point, where the population growth rate is highest, occurs when the population size is exactly half of the carrying capacity (). [1]
Considering global human expansion, factors that act as limiting forces are complex and interwoven. Historically, disease controlled human numbers severely. [4] Today, while technological advances have pushed the potential carrying capacity upward, resource availability, climate stability, and land use patterns act as increasingly prominent constraints. [7] The growth rate for humans has actually started to slow down since the 1960s peak, suggesting we are moving into a phase that resembles logistic growth on a global scale, even if specific regions continue to experience rapid expansion. [8]
# Why Growth Matters
Understanding exponential dynamics is crucial because the time it takes for a population to double becomes shorter and shorter as the growth rate increases. [5] This phenomenon is not just an academic curiosity; it has direct, tangible consequences for resource management and planning. [5]
For example, when a community or ecosystem is dealing with a process that grows exponentially—whether it is the spread of an invasive species, the proliferation of a virus, or the increasing demand for a finite resource like clean water—the early stages are often characterized by deceptive slowness. [5][9] Because the absolute numbers are small initially, the problem can seem manageable or even negligible. [5] However, because the growth is compounding, by the time the numbers are large enough to be obviously alarming, the rate of increase is so high that immediate, drastic intervention is often required, and it may be too late for mild measures to be effective. [9]
To illustrate this non-linearity, consider two scenarios of population growth over just 100 years:
| Scenario | Initial Population | Annual Growth Rate | Population After 100 Years |
|---|---|---|---|
| Slow/Linear | 10,000 | Add 200/year (2% initially) | 30,000 |
| Exponential | 10,000 | Constant 2% growth (r=0.02) | ~72,450 |
| [5] |
The difference between the linear projection (a steady addition) and the exponential projection (a compounding multiplication) is enormous by the end of the century. [5] This discrepancy highlights why simply extrapolating the current rate forward using simple addition severely underestimates future impact, whether that impact is positive (like a booming economy) or negative (like pollution accumulation or resource depletion). [9][7]
# Spotting Patterns
Recognizing exponential growth early is a skill, whether you are monitoring a biological culture or analyzing policy needs. [9] It requires looking past the raw numbers to examine the time it takes to add the next set of individuals. [9] If the time needed to double the population is consistently decreasing, you are observing exponential dynamics, not linear ones. [9]
In a medical context, this is often described using the "Rule of 70" for estimating doubling time: Divide 70 by the percentage growth rate () to find the approximate number of time periods it takes to double. [9] While this rule is often applied to finances, it works for any process exhibiting a constant percentage increase. [9] If a local disease outbreak has a growth rate of 10% per day, it doubles roughly every 7 days (). If that rate is sustained, within a month, a handful of cases can become hundreds, then thousands. [9]
For communities planning for infrastructure, recognizing that growth is exponential (or near-exponential) means that standard linear budgeting for water treatment plants or school capacity will invariably result in severe underestimation down the line. [7] If a city is projected to grow at 1.5% per year, that might sound manageable, but at that rate, the population will double in under 47 years (). [9] This necessitates planning for twice the current capacity, not just a 50% increase, over that less-than-50-year timeframe. [7] Understanding this mathematical reality forces planners to incorporate resource buffer zones and adaptive strategies much earlier than if they assumed a simple, additive growth model. [5] It shifts the perspective from "How many more people next year?" to "When will we need twice the current capacity?". [5]
Related Questions
#Citations
Exponential & logistic growth - Khan Academy
Exponential growth - Wikipedia
How Populations Grow: The Exponential and Logistic Equations
What made the world population increase so drastically after 1900?
Exponential Growth | Critical Understanding - Population Education
45.2A: Exponential Population Growth - Biology LibreTexts
[PDF] exponential growth. The human population grew at the slow rate of ...
How has world population growth changed over time?
Exponential growth: what it is, why it matters, and how to spot it

