Did Albert Einstein solve the Riemann hypothesis?
The popular image of genius often merges disparate achievements, and perhaps no two concepts are more frequently linked in popular science than Albert Einstein and the Riemann Hypothesis. While Einstein’s revolutionary work fundamentally reshaped physics by adopting and adapting the geometry pioneered by Bernhard Riemann, the assertion that Einstein solved the formidable Riemann Hypothesis is incorrect. The physicist did not claim to solve it, nor is it listed among his proven theorems. The two monumental achievements—General Relativity and the Riemann Hypothesis—originate from the same fertile mind of Riemann, but they inhabit vastly different mathematical landscapes.
# Relativity Connection

The profound link between Einstein and Riemann lies in the area of geometry. Before Einstein could formulate his theory of General Relativity, which describes gravity not as a force but as the curvature of spacetime, he needed a mathematical language capable of handling dynamic, non-Euclidean surfaces. That language was provided by the work of Bernhard Riemann, specifically his foundational concept of Riemannian geometry.
Riemann, working decades before Einstein, developed the mathematics necessary to describe spaces that could curve, bend, and warp based on the distribution of mass and energy within them. This was a theoretical leap concerning manifolds and curvature tensors. When Einstein was seeking a geometric description for his field equations, he turned to the work of mathematicians like Riemann, whose concepts perfectly described the dynamic arena of the cosmos. In essence, Riemann provided the mapmaking tools; Einstein famously used those tools to map the gravitational field of the universe. This adoption of Riemannian geometry is one of the highest tributes a physicist can pay to a mathematician's abstract work.
# The Zeta Function

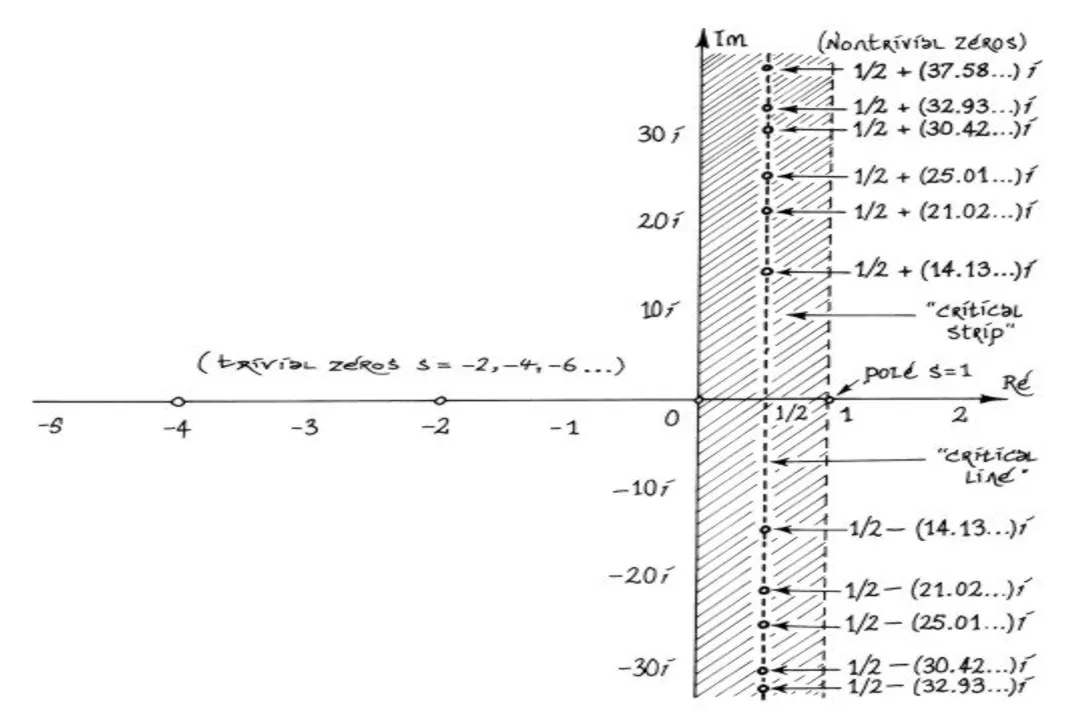
However, the Riemann Hypothesis itself concerns something entirely different: the distribution of prime numbers, anchored in complex analysis and the behavior of the Riemann zeta function, . Riemann introduced this function in his landmark 1859 paper. While that same paper is a cornerstone of geometry for Einstein, its focus regarding the hypothesis is purely number-theoretic.
The hypothesis centers on the nontrivial zeros of this zeta function. These are the complex numbers where . Riemann conjectured that all of these nontrivial zeros must lie on the "critical line," where the real part of the complex number is exactly one-half (). Proving this single statement would unlock deep secrets about how prime numbers are scattered along the number line. The challenge lies in manipulating the complex analytic properties of the zeta function, which is a far cry from calculating spacetime curvature using metric tensors.
# Unproven Status

To be direct, the Riemann Hypothesis remains one of the most famous unsolved problems in mathematics, carrying a $1 million prize from the Clay Mathematics Institute. If Einstein, whose mathematical prowess was undeniable, had successfully proven it, that proof would be a celebrated part of his legacy, firmly placed alongside his field equations. But it is not there. Even if a modern-day mathematician with Einstein’s intellect were alive today, the tools required for this specific analytic proof might still be beyond current reach. Einstein’s success was in applying existing, powerful geometry; solving the RH requires creating new mathematics in a field he did not specialize in.
We can observe that the skill sets required for these two achievements diverge significantly. Einstein’s triumph involved a synthesis of existing geometric ideas into a physical theory, whereas the RH demands an almost mystical understanding of the fine structure of the integers. Thinking about it from a historical perspective, while Einstein certainly possessed staggering mathematical intuition, his primary breakthroughs were rooted in physical principles compelling him toward a specific mathematical structure (geometry). The Riemann Hypothesis, conversely, is a purely internal mathematical statement about the zeros of an analytic function.
# Mathematical Value
The significance of the Riemann Hypothesis is immense for pure mathematics. Its truth would immediately validate hundreds of other theorems that begin with the conditional statement, "Assuming the Riemann Hypothesis is true, then...". These dependent results span cryptography, theoretical computer science, and deep number theory, all hinging on the precise locations of those zeta function zeros. If proved, it would offer the tightest possible estimates for the distribution of prime numbers, effectively mapping their randomness with high precision.
The tantalizing mystery surrounding the proof has even led some to speculate about lost knowledge. There is academic discussion regarding the potential importance of Riemann's own lost notes—sometimes referred to as a "missing black book"—which might contain clues about his original intent or unstated insights regarding the hypothesis. While this remains speculative, it underscores the depth of the problem and the high value placed on any possible key to its solution.
# Divergent Fields
It is interesting to note how easily the fields are confused. A general reader looking at the immense contribution of Riemann to the physics of Einstein might naturally assume that since Einstein successfully used Riemann’s work for relativity, he must have mastered all of Riemann’s work, including the unsolved conjecture. This is a common error when dealing with figures of such monumental stature—the tendency to attribute total mastery of a related concept to the known genius. The fact that Riemann’s name is attached to both concepts, separated by decades and different mathematical domains (geometry versus analytic number theory), further fuels this misconception.
If we were to create a hypothetical performance comparison, it might look something like this, based on their respective domains:
| Concept | Creator | Field | Einstein's Role | Status |
|---|---|---|---|---|
| Riemannian Geometry | Riemann | Differential Geometry | Adopted and applied to physics (GR) | Proven Fundamental |
| Riemann Hypothesis | Riemann | Analytic Number Theory | Did not address or solve | Unproven |
This comparison highlights that Einstein was the master synthesizer and applier of geometrical concepts, not necessarily the master analyst of zeta functions.
# The Creative Gap
Consider the difficulty from a creative standpoint. Einstein’s 1915 breakthrough represented an astonishing physical insight translated into a geometric language already available in principle. It required genius to see the connection between gravity and curvature. Solving the Riemann Hypothesis, however, is thought to require a novel conceptual breakthrough in the very nature of complex functions and prime numbers, something that has eluded the best mathematical minds for over 160 years.
It is plausible that the kind of insight needed to prove the RH is fundamentally different from the kind of insight needed to formulate General Relativity. One requires seeing the large-scale structure of the universe through warped space; the other requires mapping the erratic, microscopic distribution of the building blocks of arithmetic. While both demand extraordinary intelligence, they seem to call for different types of mathematical vision. The world still awaits the mind—whether it be a contemporary Einstein or a mathematical pioneer entirely new—who can finally place all those mysterious zeros onto the critical line.
#Videos
Riemann's Influence on Einstein's Theory of Relativity Explained
Related Questions
#Citations
Einstein Couldn't Solve This Math Problem, Can You? - Medium
Had Einstein been alive today and become a mathematician, would ...
How Did Einstein Use Riemann's Geometry To Develop Theory Of ...
The Inspiring Story of the Man Whose Math Led To The Formulation ...
FYI..... There's a math question called the Riemann Hypothesis ...
Bernhard Riemann, The Mind Who Laid the Foundations for ...
Riemann's Influence on Einstein's Theory of Relativity Explained
What is the real importance of the missing black book of Riemann's ...
The Riemann Hypothesis
What does proving the Riemann Hypothesis accomplish?