Did Yitang Zhang solve the Riemann hypothesis?

The mathematical community often experiences intense bursts of energy followed by periods of quiet scrutiny, and few figures inspire such a rapid swing as Yitang Zhang. When news broke that the mathematician who dramatically reduced the gap between prime numbers had turned his attention to the Riemann Hypothesis (RH), the excitement was palpable. The sheer weight of the RH—one of the most famous and difficult unsolved problems in mathematics—means any credible claim toward its solution immediately captures global attention. ^[8] However, pinning down whether Zhang has solved the hypothesis requires separating initial announcements from final, peer-reviewed consensus.

# Prime Gaps Fame

To understand the weight behind the recent claims, one must remember Zhang’s established place in modern mathematics, cemented in 2013. Before tackling the legendary RH, Zhang achieved a massive breakthrough concerning the spacing between prime numbers. ^[3] For centuries, mathematicians knew that while primes thin out as numbers get larger, they never truly stop appearing. The critical question was whether there were infinitely many pairs of primes separated by a fixed, finite distance.

Zhang proved that there are infinitely many pairs of prime numbers separated by a gap of no more than $70$ million. ^[3][4] This was revolutionary because it proved that prime gaps are bounded, even if the bound ($70$ million) was large. This work solved a long-standing problem, narrowing a gap that had stubbornly resisted mathematicians for decades. ^[4] His achievement demonstrated extraordinary technical skill in analytic number theory, particularly involving sieving methods. This success serves as the foundation of trust for his subsequent, even grander claims. ^[2]

# New Claim Emerged

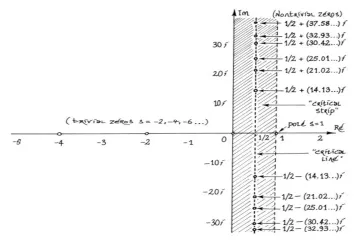
The latest developments, surfacing around late 2022 and into 2023, suggested Zhang was aiming even higher, setting his sights squarely on the Riemann Hypothesis. ^[3][7] The Riemann Hypothesis, formulated in 1859, deals with the distribution of the non-trivial zeros of the Riemann zeta function, stating they all lie on the "critical line" where the real part of the complex variable is $1/2$. ^[8] Proving this would instantly unlock solutions to countless other problems in number theory related to the distribution of prime numbers. ^[8]

What Zhang reportedly presented was a new manuscript, described by some as a major breakthrough that might offer a path toward resolving the RH or a closely related, highly difficult problem, such as proving the non-existence of Landau–Siegel zeros. ^[4][5] The connection between the Riemann Hypothesis and the Landau–Siegel zeros is deep; ruling out these specific types of zeroes is equivalent to proving a certain version of the RH regarding number fields. ^[5] The initial reports were characterized by high anticipation, with some commentators suggesting a potential solution was near. ^[6]

Did Albert Einstein solve the Riemann hypothesis?

# Hypothesis Stakes

The distinction between Zhang’s established work and his new endeavor is crucial for appreciating the scale of the claim. His 2013 success involved proving a finite bound on the gaps between some primes. While staggering, it was a specific application of deep techniques. The Riemann Hypothesis, conversely, is an assertion about an infinite set of complex numbers—the zeros of the zeta function—and it lies at the very bedrock of analytic number theory. ^[8]

If the RH is true, the distribution of prime numbers is as regular as mathematically possible. If it were false, many theorems currently proven assuming the RH would instantly collapse or require massive revision. This is why a proof is worth a million dollars (the Clay Millennium Prize) and eternal mathematical glory. ^[8]

It is interesting to reflect on the nature of these deep problems. Proving the bounded prime gap involved mastering existing sieve theory and adding a decisive new ingredient. Solving the RH, however, often feels less like adding a finishing touch and more like discovering an entirely new continent of mathematics from which to launch an attack. When Zhang reported his new work, the mathematics world immediately started assessing if he had invented this new continent or merely found an incredibly advanced mapping technique for the known terrain. ^[2]

# Scrutiny Process

In mathematics, particularly for Millennium Prize problems, a claim is not a solution until it has survived a brutal, multi-stage vetting process. The process is deliberately slow to ensure accuracy, a practice essential for maintaining the integrity of the field. ^[1]

When Zhang released his preliminary findings, the immediate reaction was a mix of hope and healthy skepticism. One common path involves posting pre-prints for open peer review, a stage where the community attempts to find flaws, contradictions, or gaps in logic. ^[1] For a claim as monumental as solving the RH, the scrutiny is intense, often involving dozens of specialists reading the argument line-by-line over many months, sometimes years. ^[2]

One source confirmed that following Zhang’s announcement, mathematicians quickly worked to verify his claims, often starting by focusing on whether his arguments concerning the Landau–Siegel zeroes were sound, given their deep linkage to the RH. ^[5] This initial review phase is where many promising claims fail. The key here is that confirmation of partial results can happen much faster than confirmation of the entire proof.

What defines a scientific hypothesis?

# Current Status Assessment

Based on the information circulating after the announcement, it appears that Yitang Zhang has not been officially recognized as having solved the Riemann Hypothesis outright. ^[2] What has happened, according to reports, is the confirmation of parts of his work. ^[1] Specifically, some experts confirmed that certain intermediate steps or related conjectures presented in his broader theory hold true. ^[1] This is a massive achievement in itself, suggesting Zhang has indeed found a significant new mathematical tool or argument. ^[7]

However, this confirmation of sub-theorems does not equate to a verified proof of the central hypothesis itself. Many prominent mathematicians, when asked for an opinion on the correctness of the full proof, tended to adopt a cautious stance, waiting for the final, comprehensive, and accepted write-up. ^[2] The gap between "a convincing new argument that solves a piece of the puzzle" and "the definitive, accepted proof of the Riemann Hypothesis" is vast.

For instance, consider this comparison: If you are trying to build a skyscraper (the RH), and Zhang presents a revolutionary new concrete mixture (a sub-theorem) that the engineers confirm is sound, that’s a major win. But until the structure is fully poured, cured, and inspected according to the original blueprint, the building isn't officially complete. The sheer difficulty means that even if Zhang has solved a major component related to the zeroes, the final logical leap to cover all zeros might still be outstanding or require further external validation.

It’s also important to note the historical pattern. The mathematical world is littered with premature announcements regarding major conjectures. In the case of the RH, there have been numerous "solutions" over the decades, all of which eventually contained fatal flaws upon deeper inspection. ^[5] This historical precedent necessitates extreme caution; trust must be built on reproducibility and consensus, not just initial excitement.

# Insight into Verification Speed

The speed at which new mathematical results are accepted often depends on the tools used. If Zhang employed methods similar to his 2013 proof, the community might recognize the machinery quickly. However, if his approach to the RH required truly novel concepts—a necessity for such a hard problem—the time required for comprehension explodes. An expert might need weeks just to grasp the notation of a new area, let alone verify its correctness. When dealing with a problem like the RH, which is so tightly woven into the fabric of existing number theory, a truly new method might require the entire field to slow down and learn a new language before they can even begin the verification process. This is likely why progress toward full acceptance is measured in months or years, even when the initial excitement is high.

In summary, Yitang Zhang has solidified his reputation as one of the preeminent mathematicians of his generation through verifiable, monumental work. ^[3] His recent claims regarding the Riemann Hypothesis have led to confirmed breakthroughs in related areas, suggesting he is operating at an incredibly high level. ^[1][7] Yet, as of the latest consensus derived from the community's response, the full, universally accepted solution to the Riemann Hypothesis remains an open, albeit much closer, problem. The world of mathematics is waiting for the final page of that story.