If a function exhibits chaotic, infinitely oscillating behavior, how does this affect the network's approximation?
Answer
Achieving a high degree of accuracy becomes extremely difficult, even for very large networks.
Functions possessing sharp discontinuities or chaotic behavior are cited as examples that present practical and theoretical boundaries to what neural networks approximate easily, even with large sizes.
#Videos
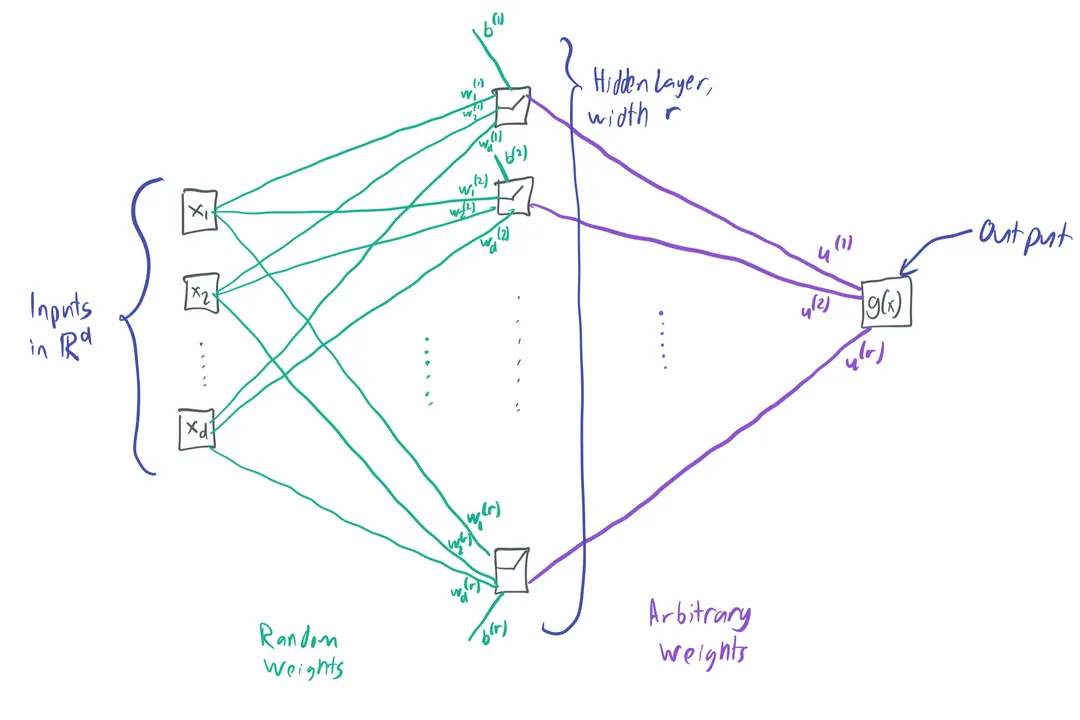
Why Neural Networks Can Learn Any Function - YouTube
Related Questions
What mathematical theorem summarizes the foundation of a neural network's ability to model complex relationships?According to the UAT, what must the activation function be to grant a network universal approximation power?What limitation occurs if the activation function used in a network were only a simple polynomial?What is a key structural prerequisite for the standard feedforward network described by the UAT?How does a single neuron, utilizing a non-linear activation, function conceptually within the network's approximation process?What specific type of region must the input domain belong to for the UAT to guarantee approximation of any continuous function?What advantage does network depth (multiple hidden layers) offer over extreme width in a shallow network?What does the UAT guarantee regarding the process of finding the specific weights and biases?What common optimization challenge can prevent gradient descent from reaching the desired level of accuracy specified by the UAT?If a function exhibits chaotic, infinitely oscillating behavior, how does this affect the network's approximation?How is the overall success of a neural network approximation measured according to the text?