How do neural networks approximate functions?

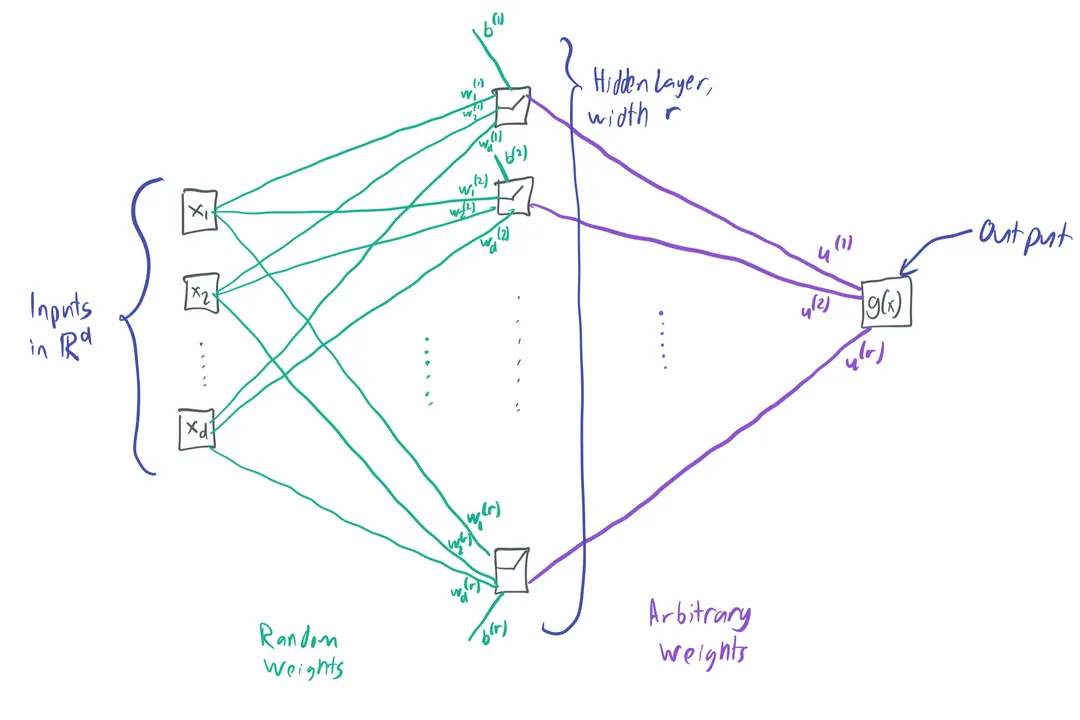
The ability of a neural network to model complex relationships—to essentially mimic any mathematical process we feed it—is one of the most fascinating aspects of deep learning. This capability isn't magic; it rests on a firm mathematical foundation, primarily summarized by the Universal Approximation Theorem (UAT). ^[1][9] Simply put, a sufficiently large neural network can approximate any continuous function to any desired degree of accuracy, provided the right ingredients are present. ^[1]

The practical question is how this approximation happens. It’s less about the network finding an exact formula and more about it meticulously piecing together simple transformations until the output matches the target function across its input domain. ^[4]

# Approximation Guarantee

The cornerstone of this concept is the UAT itself. This theorem asserts that a standard feedforward network containing a single hidden layer, with a finite, albeit potentially large, number of neurons, can approximate any continuous function defined on a compact (closed and bounded) subset of ${\mathbb{R}}^n\backslash mathbb\{R\}^n$. ^[1] Think of a compact set as any finite region of possible inputs you could draw on a graph—it has defined boundaries. ^[1]

Crucially, this powerful claim has specific prerequisites. The network must be a feedforward structure, meaning the information moves strictly in one direction without loops. ^[1] The approximation capability hinges on the activation function used in the hidden layer. ^[9] This function must be non-polynomial, such as the ubiquitous sigmoid or the more modern Rectified Linear Unit (ReLU). ^[1][8] If the activation were just a simple polynomial (like $x^{2}x^2$ or $x^{3}x^3$), the entire network, no matter how many layers or neurons it stacked, would still only be capable of representing another polynomial function, severely limiting its utility. ^[1]

# Activation Function Role

The activation function is the non-linearity that grants the network its approximation power. Without it, multiple layers simply collapse into a single linear transformation, meaning the network could only ever model straight lines or simple planes. ^[8]

The non-polynomial nature of the activation allows the network to bend and curve its mapping. Consider a function that needs to create a sharp corner or a sudden jump in output. A single neuron, operating with a non-linear activation like the sigmoid (which smoothly transitions from near zero to near one), acts like a soft switch or a localized "probe" in the input space. ^[6] By carefully placing many of these probes (neurons) in the hidden layer and adjusting their associated weights and biases, the network essentially builds a piecewise function. ^[8]

Imagine you need to draw a perfect circle on a piece of graph paper. You cannot do it with just one straight line. Instead, you approximate it by drawing many incredibly short, straight line segments connecting points along the desired curve. In a single-hidden-layer network, each neuron contributes one of these localized, curved segments to the final output. The network learns the exact location (bias) and steepness (weights) of each segment required to stitch together the final, complex approximation. ^[6] The more neurons you have, the more small, localized pieces you can use, leading to a finer approximation of the true function. ^[1]

How does the eye convert light into neural signals?

# Depth Efficiency

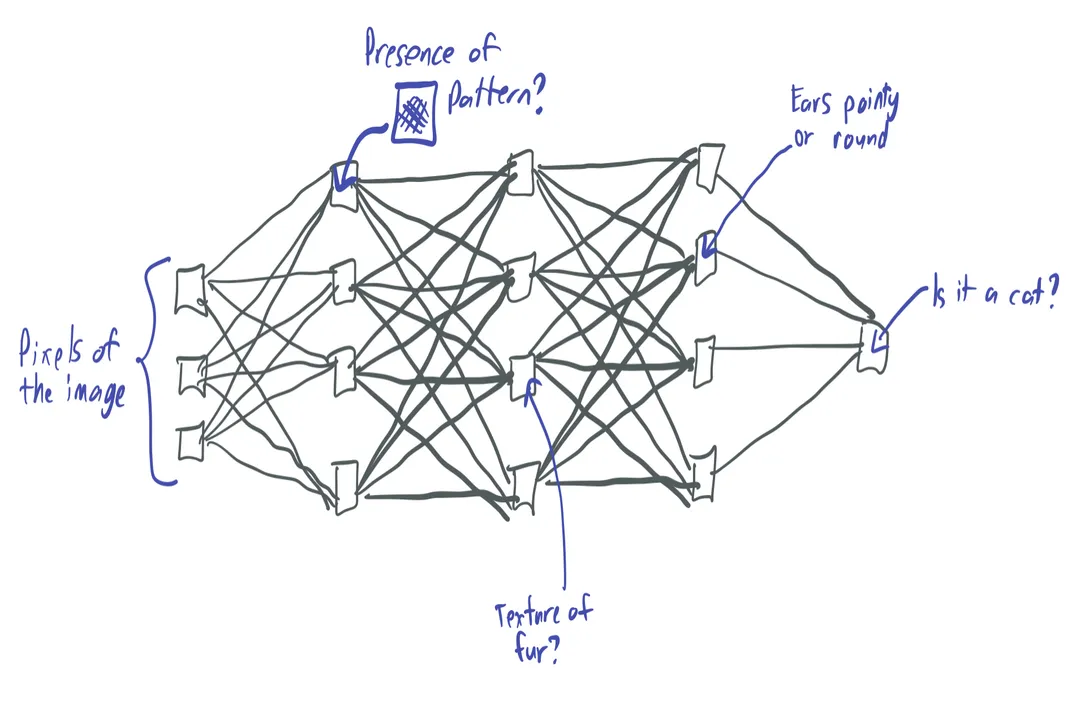
While the UAT confirms that a single hidden layer is theoretically sufficient, it does not comment on how many neurons that layer needs. For certain complicated functions, approximating them with just one layer might require an exponentially huge number of neurons relative to the input dimension. ^[6] This is where the structure of deep networks—those with multiple hidden layers—shines.

Depth offers a significant computational and representational advantage over sheer width in a shallow network. ^[6] Deep architectures can represent many functions much more compactly than their shallow counterparts, meaning they need far fewer total parameters (weights and biases) to achieve the same level of approximation accuracy. ^[6]

For instance, representing a hierarchical structure, like a complex image feature (edges combine to form shapes, shapes combine to form objects), is naturally mapped onto a deep stack. Each successive layer builds upon the abstractions learned by the previous one. While a wide, shallow network could theoretically map the same function, it would require an explosion in the number of nodes in that single layer, making the resulting model unwieldy, prone to overfitting, and vastly more expensive to train. ^[6] In essence, depth provides a structural shortcut for learning compositional functions, achieving functional equivalence with much less effort than a very wide, flat structure. ^[6]

# Training Reality Check

The UAT is a statement of existence: a set of weights and biases exists that makes the network approximate the function well. ^[3] However, the theorem offers absolutely no practical guidance on how to find those specific values. This is where the actual process of training, typically using gradient descent, comes into play. ^[3]

The theoretical guarantee is often independent of the learning algorithm used. If the network structure is set up correctly (one hidden layer, non-polynomial activation), the function space we are searching within contains the target function. ^[1] The difficulty lies in navigating the loss landscape—the error surface defined by the difference between the network's output and the true function. ^[3]

When a human or an algorithm sets the initial weights randomly, the network starts somewhere arbitrary on this error surface. Gradient descent then attempts to "walk downhill" toward the minimum error. Even if the global minimum (the perfect approximation) exists, the optimization process can get stuck in a local minimum—a valley that is low but not the lowest point across the entire landscape. ^[3] The network has approximated the function well, but not to the desired degree of accuracy specified by the theorem's $ϵ\backslash epsilon$ tolerance. ^[1]

A useful way to think about this is comparing setting up the network architecture to commissioning an architect. The UAT confirms that a building exists that meets the specifications (the function). Training, then, is the construction crew trying to build it without a perfect blueprint, hoping they don't accidentally build a serviceable shed instead of the intended skyscraper, even though the specifications guarantee the skyscraper is possible to build. The difficulty of training often reflects the complexity of the target function itself, not a failure of the network's potential. ^[6]

How does ultrasound imaging function?

# Approximation Limits

While neural networks are universal function approximators, there are practical and theoretical boundaries to what they approximate easily or efficiently. ^[4]

The theorem applies cleanly to continuous functions on compact sets. ^[1] If the function you are trying to approximate has sharp discontinuities (like a perfect step function) or exhibits chaotic, infinitely oscillating behavior within the input domain, achieving a high degree of accuracy becomes extremely difficult, even for very large networks. ^[4]

For a function with a jump, a network built from smooth, continuous activation functions (like sigmoid) must use a large number of neurons to create a steep enough "wall" that approximates the discontinuity. ^[8] You can get very close, but because the individual components are smooth, the resulting approximation will have some small error right at the point of the jump. Networks are great at modeling smooth phenomena but struggle with sharp breaks unless specifically designed (e.g., using specialized activation functions or architectural tricks). ^[4]

Furthermore, it is vital to remember the measure of success: the approximation is defined by its maximum error over the entire input region—the supremum norm. ^[1] A network might be excellent everywhere except for one tiny spot where the error spikes up dramatically. This single spike, if large enough, can mean the approximation fails the overall test, even if it looks perfect to the naked eye across 99.9% of the domain. ^[1] This underscores why selecting the right size and topology for the network is an empirical decision, even when theory suggests it can be done. ^[6]