What governs crystal lattice formation?
The orderly arrangement of matter into a crystal lattice is a fundamental property of many solids, a pattern defined by the periodic, repeating three-dimensional structure of its constituent atoms, ions, or molecules. [1][7][8] This seemingly simple organization—a lattice of points that repeats in space—is not arbitrary; it is strictly governed by a delicate interplay of fundamental forces, energy minimization principles, and the kinetics of the formation process itself. Understanding what dictates the final architecture requires looking at the chemistry that holds the material together and the physics that dictates how it settles into its lowest energy configuration. [5][6]
# Bonding Forces
The initial and perhaps most decisive factor governing how any crystalline material organizes itself stems from the nature of the chemical bonds present. [1] These bonds determine the distance between neighboring components and the strength of their interaction, which fundamentally constrains the possibilities for lattice formation.
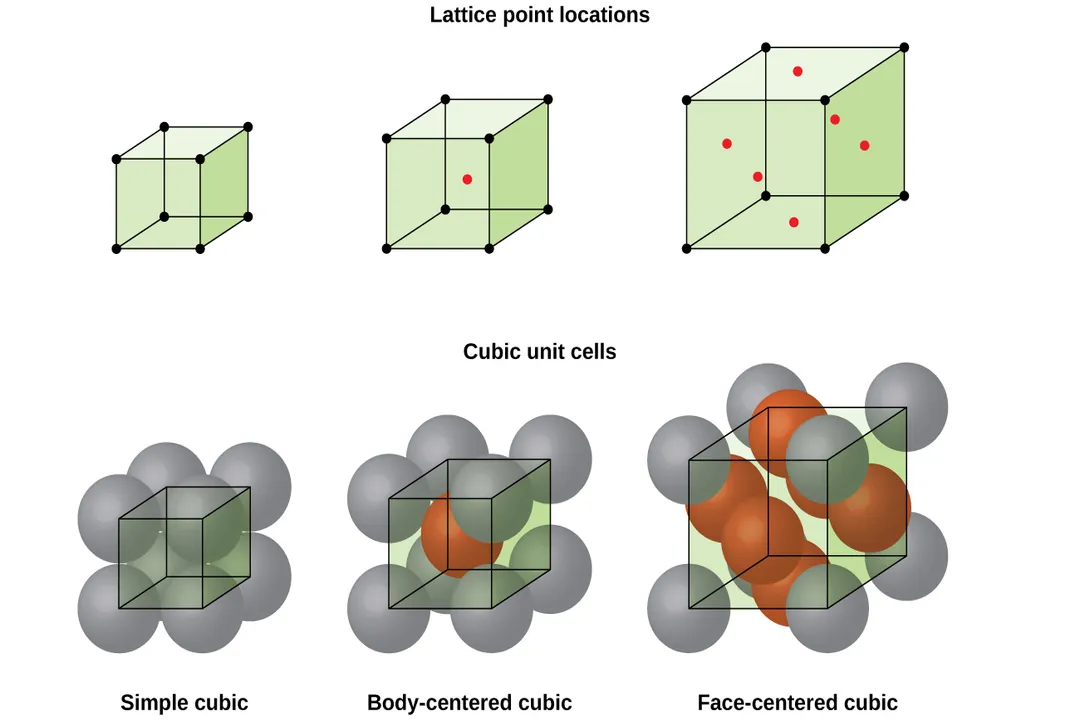
For ionic compounds, the structure is overwhelmingly dictated by electrostatic attraction between oppositely charged ions. [1] The arrangement strives to maximize the number of nearest neighbors of the opposite charge while minimizing the repulsion between like charges. This balance leads directly to specific coordination numbers and geometries, such as the familiar rock salt (NaCl) structure, where each sodium ion is surrounded by six chloride ions, and vice versa, creating a face-centered cubic arrangement overall. [2]
In contrast, materials held together by covalent bonds, like diamond or quartz, often have structures dictated more by the fixed geometry of the directional bonds themselves. A carbon atom in a diamond lattice forms four specific directional bonds arranged tetrahedrally. This strong, directional requirement pre-determines the lattice geometry, making it less susceptible to simple close-packing rules that govern non-directional bonds. [9]
Metallic solids exhibit yet another governing principle: the delocalized sea of electrons. While still seeking low-energy arrangements, metals often default to the densest possible packing arrangements, such as the Face-Centered Cubic (FCC) or Body-Centered Cubic (BCC) lattices, because the bonding forces are less directionally specific than covalent bonds. [2][5]
The structural outcome is a direct reflection of the bond type:
| Bond Type | Primary Governing Constraint | Typical Packing Tendency |
|---|---|---|
| Ionic | Electrostatic attraction/repulsion | Geometries dictated by radius ratio |
| Covalent | Fixed bond angles and distance | Determined by orbital hybridization |
| Metallic | Non-directional attraction | Maximizing atomic density (e.g., FCC, HCP) |
This inherent chemical underpinning determines who can occupy which site relative to their neighbors.
# Minimum Energy
The ultimate goal for any system, including a solid forming from a liquid or gas, is to achieve the lowest possible potential energy state, which aligns with thermodynamic stability. [5][6] Crystal lattice formation is a process where the components arrange themselves in the most energetically favorable 3D pattern.
When a substance transitions from a disordered state (like a liquid) to an ordered crystalline solid, there is a significant release of energy, often referred to as the latent heat of fusion. This release corresponds to the formation of stronger, more stable bonds across the entire structure. [6] The specific lattice structure adopted—be it simple cubic, FCC, or hexagonal—is the one that yields the absolute minimum potential energy for the given set of atoms or ions under those specific temperature and pressure conditions. [1]
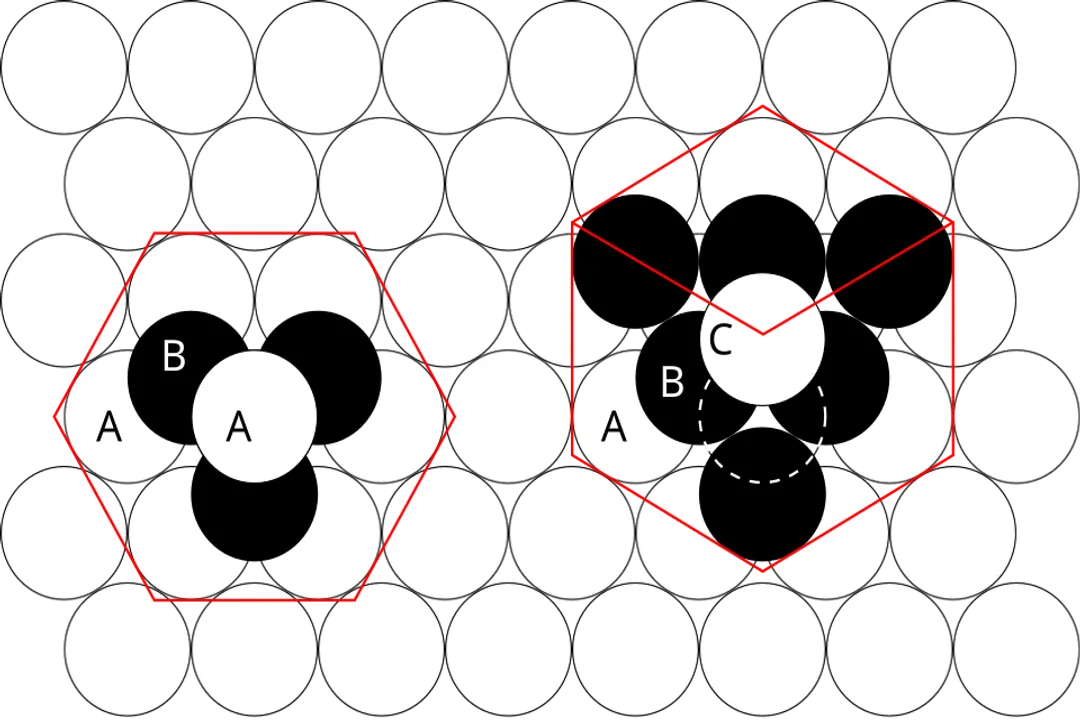
The concept of space filling is tightly linked to energy minimization. In systems where attraction is non-directional, like noble gas solids or many metals, the arrangement that allows the largest number of atoms to be packed into the smallest volume—thereby maximizing favorable short-range interactions—will be the preferred structure. [1] The FCC and hexagonal close-packed (HCP) structures are the most efficient ways to pack identical spheres, each achieving a packing efficiency of approximately 74%. [2] Any other configuration would result in unused space and higher potential energy.
It is interesting to observe how this energy drive influences materials with slightly different components. For instance, consider two hypothetical alkali halides, one with very similar-sized ions and one with very dissimilar sizes. The former might easily settle into the simple cubic lattice, while the latter might have to adopt a larger unit cell or a structure with a lower coordination number (fewer neighbors) to maintain charge neutrality and avoid overwhelming repulsive forces, even if that structure is slightly less dense overall. [1] The energy minimum is a complex balance, not just a simple density maximization.
# Packing Shapes

Beyond the fundamental forces, the geometry of the components imposes rigid rules on the resulting structure. This is particularly evident in the classification of crystal systems based on symmetry and lattice points. [3][4]
The geometry of the structure is often described using the Bravais lattice, which defines the 14 unique ways that points can be arranged periodically in three dimensions. [3] When combined with the atoms (the basis) located at those points, we get the complete crystal structure. [9] The constraints imposed by the size and shape of the building blocks directly determine which of the seven crystal systems (cubic, tetragonal, orthorhombic, etc.) the material can adopt. [4]
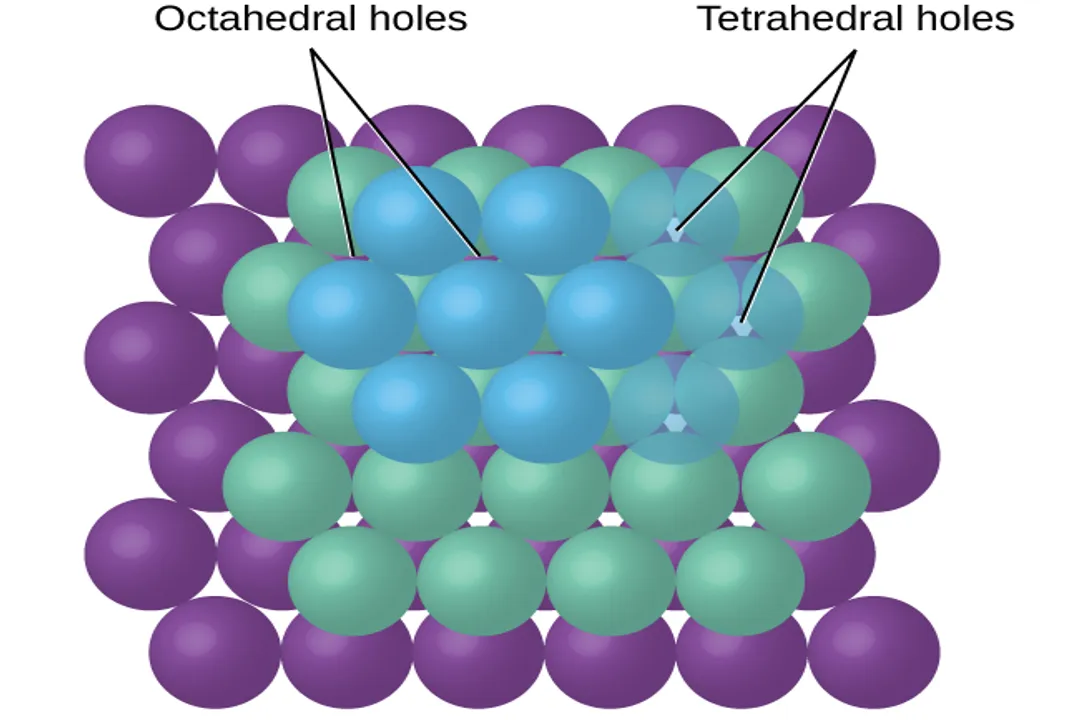
For instance, in ionic crystals, the ionic radius ratio (the ratio of the cation radius to the anion radius) is a critical dictator of the resulting geometry. If the radius ratio falls within a certain narrow range, the ions can coordinate in a specific way—perhaps a tetrahedral arrangement with a coordination number of four. If the cation is significantly smaller, it might not be able to touch all the surrounding anions, leading to a lower coordination number structure (like square planar) or structural instability. [1] A deviation outside the acceptable ratio forces a structural change to maintain electrical neutrality and structural integrity, even if it seems less geometrically obvious than close packing. [1]
# Cooling Rate
While chemistry and thermodynamics set the possible structures, the kinetics of the process—how quickly the solid forms—governs which of those possibilities is actually realized. This is where the transition from liquid to solid, or crystallization, becomes crucial. [6]
If the material is cooled very slowly, the atoms or ions have ample time to diffuse, explore different local arrangements, and settle into the configuration that corresponds to the true thermodynamic minimum energy state, resulting in large, well-formed crystals with low defect densities. [6] This slow movement allows the system to overcome kinetic barriers that might trap it in a higher-energy arrangement.
Conversely, rapid cooling—quenching—traps the atoms in a configuration dictated by the speed of the process rather than the lowest energy state. This often results in a glassy or amorphous solid, where there is no long-range periodic order. [6] If cooling is intermediate, the result is often a polycrystalline material composed of many small, randomly oriented crystalline grains.
Consider the case of silicon used in semiconductor manufacturing. Achieving the near-perfect single-crystal structure necessary for high-performance electronics requires extremely slow, controlled growth rates from a melt. A slight acceleration in the pulling rate can introduce twinning defects or dislocations—regions where the lattice symmetry is locally broken—because the material is forced to incorporate atoms faster than they can find their lowest energy neighbors. [6] This highlights that the formation process is not just about what the minimum energy structure is, but how the system navigates the pathway to get there.
# Structural Rules
The governing factors coalesce into specific rules that classify and predict lattice formation. The concept of symmetry operations—rotations, reflections, and inversions—is essential for defining the possible lattices. [3][9] A crystal structure must be perfectly periodic and possess translational symmetry, meaning that if you move the entire crystal by a specific vector, it looks exactly the same. [7] This requirement limits the number of geometrically possible arrangements to the 14 Bravais lattices and the corresponding point groups. [3][9]
The physical characteristics of the constituent particles are often simplified into idealized models to understand these rules. For example, treating ions as hard spheres allows scientists to use concepts like the coordination number—the number of nearest neighbors touching a central atom—as a direct proxy for the local packing efficiency and, therefore, the stability of the structure. [2]
When building large, high-quality single crystals for research or industrial application, a key challenge that speaks directly to the governing rules is managing the introduction of imperfections. While we aim for the ideal lattice, real systems are rarely pure or perfectly cooled. Even minute amounts of impurities can act as nucleation sites or local energy traps, altering the preferred growth path. A crystal engineer must carefully control temperature gradients and impurity levels to ensure that the desired, thermodynamically favored lattice structure continues to grow outwards from the seed crystal without being derailed by kinetic noise or local chemical variations. [6] The resulting lattice is therefore a compromise between the strict geometric demands of the bonding and the practical limitations imposed by the rate of cooling and the purity of the material being crystallized.
Related Questions
#Citations
Crystal Lattice — Structure & Formation - Expii
10.6: Lattice Structures in Crystalline Solids - Chemistry LibreTexts
Crystal structure - Wikipedia
Types of Crystal Lattices - The Natural Gemstone Company
Revision Notes - Crystal Lattice Structures | Chemistry | AP - Sparkl
Crystallization: The Beauty of Organization
Crystal lattice - Crystal growing wiki
Crystal lattice - Inorganic Chemistry II Key Term - Fiveable
Crystal structure – Knowledge and References - Taylor & Francis