How does pressure vary with depth in fluids?

This fundamental concept, how pressure changes as you descend into a body of water, air, or any fluid, is one of the cornerstones of fluid mechanics, dictating everything from how deep a submarine can dive to why your ears feel funny on an airplane. ^[1][7] At its simplest, the increase in pressure with depth stems directly from the weight of the fluid resting on top of you. ^[2][5][9] Imagine a tall stack of books; the book at the very bottom supports the weight of every book above it, resulting in the highest pressure. In a fluid, this "stack" is the column of liquid or gas extending from your current depth all the way up to the surface. ^[5]

# Weight Column

When we talk about pressure within a fluid at rest—what physicists call a static fluid—we are essentially quantifying the force exerted by this overlying mass per unit area. ^[1][4][7] This force is gravity pulling down on the fluid’s mass. Because of this relationship, the pressure exerted by the fluid is directly proportional to the depth you descend. ^[1][4][7] Go twice as deep, and the weight of the fluid column above you doubles, thus doubling the pressure added by the fluid itself. ^[7]

The key factors that determine how fast this pressure increases as you move down are the fluid's density ($\rho$) and the local acceleration due to gravity ($g$). ^[1][4][7] A denser fluid packs more mass into the same volume, meaning a smaller vertical column exerts the same weight as a larger column of a less dense fluid. Conversely, if you could somehow travel to a place with significantly lower gravity, the same volume of fluid would weigh less, resulting in a slower pressure increase with depth. ^[9]

# Pressure Equation

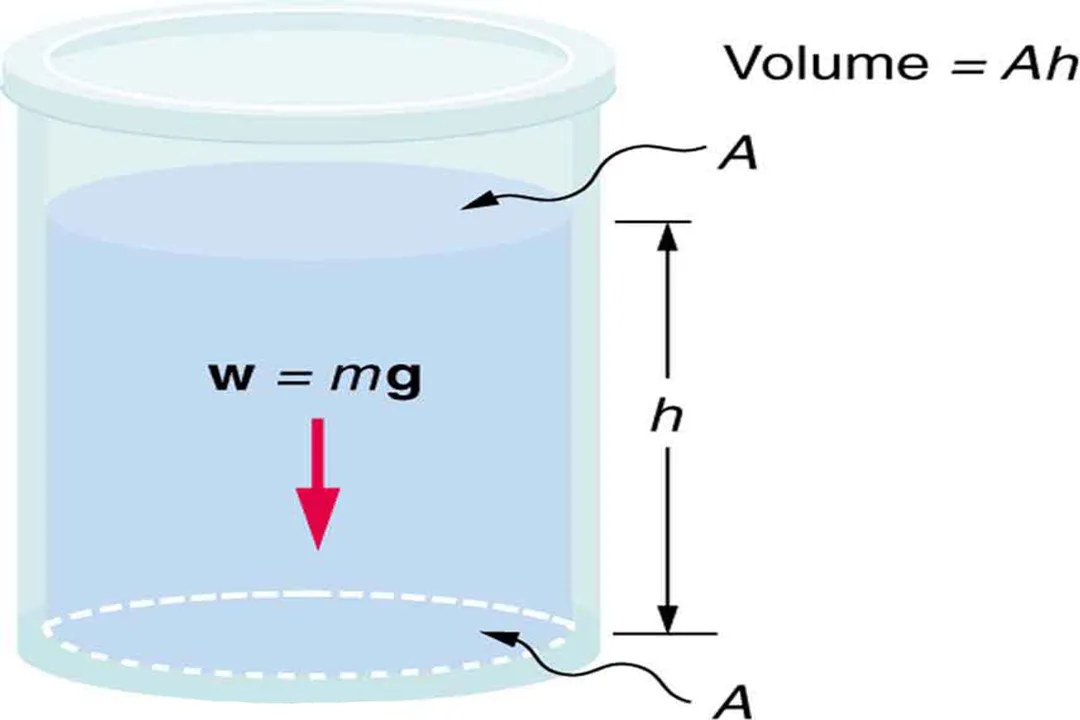
To put this principle into a usable mathematical expression, we combine these factors. The pressure ($P$) experienced at a specific depth ($h$) within a fluid is described by a straightforward linear relationship. ^[1][7] The full absolute pressure is the sum of the pressure exerted by the fluid column and the pressure already present at the surface, often denoted as $P_0$. ^[4][7]

The standard equation looks like this:

$$P = P_0 + \rho g h$$

Here, $P_0$ represents the pressure at the surface, which is typically atmospheric pressure when dealing with open containers or natural bodies of water. ^[7][9] The term $\rho g h$ is often referred to as the gauge pressure—the pressure generated purely by the fluid itself. ^[4]

This relationship is so reliable that it allows for direct comparison across different liquids. For example, at the same depth, seawater (denser) will exert a higher pressure than freshwater, and both will exert much higher pressure than a layer of motor oil (less dense). ^[4] To give a practical feel for the rate, in fresh water at standard gravity, the pressure increases by approximately one atmosphere (or $101.3$ kilopascals) for every $10.1$ meters ($\approx 33$ feet) of depth. ^[1]

If we consider an environment where the surface pressure ($P_0$) is negligible or irrelevant to the measurement being taken, such as analyzing the internal stress on a submerged pipeline far below the surface, we sometimes use the concept of pressure head, which is simply the depth ($h$) expressed in terms of the fluid’s height that would be required to produce that pressure: $h = P / (\rho g)$. ^[8] This helps engineers conceptualize the equivalent vertical distance of force being applied.

What causes osmotic pressure?

# Pressure Measurement

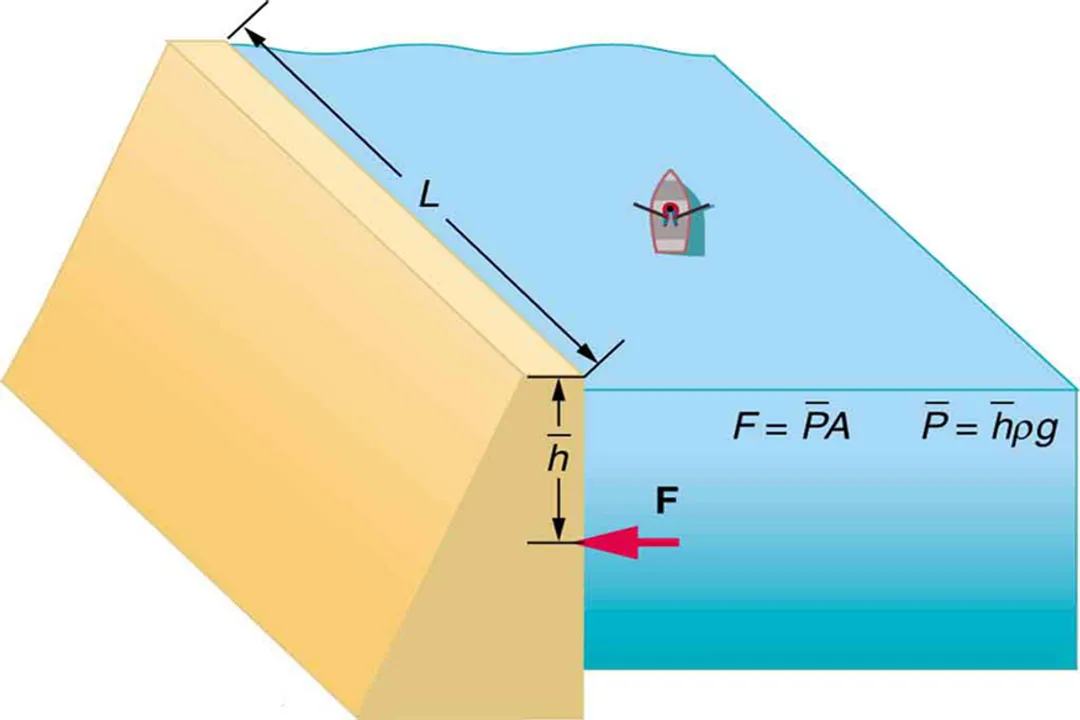
The way we talk about pressure in different contexts matters, particularly when discussing depth. It is essential to distinguish between absolute pressure and gauge pressure. ^[4][7]

• Absolute Pressure is the total pressure acting on an object, which includes both the pressure from the fluid above it and the pressure acting on the fluid’s surface (like the atmosphere). ^[4][7] This is the $P$ in the full equation: $P_{abs} = P_0 + \rho g h$.
• Gauge Pressure measures only the pressure in excess of the ambient atmospheric pressure. ^[4] In our equation, this is the $\rho g h$ portion. When you check the tire pressure on your car or use a standard diving gauge, you are reading the gauge pressure—how much the pressure inside has exceeded the outside air pressure. ^[7]

Consider a typical scenario: a researcher diving in a pool. If the atmospheric pressure ($P_0$) is $101.3 \text{ kPa}$ and the depth creates a gauge pressure ($\rho g h$) of $50 \text{ kPa}$, the absolute pressure the diver feels is $151.3 \text{ kPa}$. ^[4] Many pressure sensors are designed to measure gauge pressure directly, simplifying the data collection process unless absolute pressure calculations, such as those needed for altitude determination, are required. ^[7]

# Fluid States

The formula $P = P_0 + \rho g h$ works beautifully and simply for most liquids, such as water, because we treat them as incompressible. ^[7] Incompressible means that as you descend, the density ($\rho$) remains essentially constant because the fluid cannot be significantly squeezed into a smaller volume. ^[7]

However, this assumption breaks down when dealing with gases, like the Earth's atmosphere or the air inside a pressure vessel. ^[7] Gases are highly compressible. As you move deeper into the atmosphere (or increase the pressure inside a tank), the gas molecules are forced closer together, causing the density ($\rho$) to increase significantly. ^[7] Because $\rho$ is no longer constant, the simple linear equation is insufficient for precise calculation across large vertical distances. Calculating pressure variation in a compressible fluid often requires more advanced calculus, specifically integration, to account for the changing density at every infinitesimal step of depth. ^[7] For example, the pressure change rate near the Earth's surface is small, but the pressure difference between sea level and the top of Mount Everest is calculated using these more complex models. ^[7]

Which institute recently collaborated with ISRO to create a centre of excellence focused on research in Fluid and thermal sciences?

# Real World

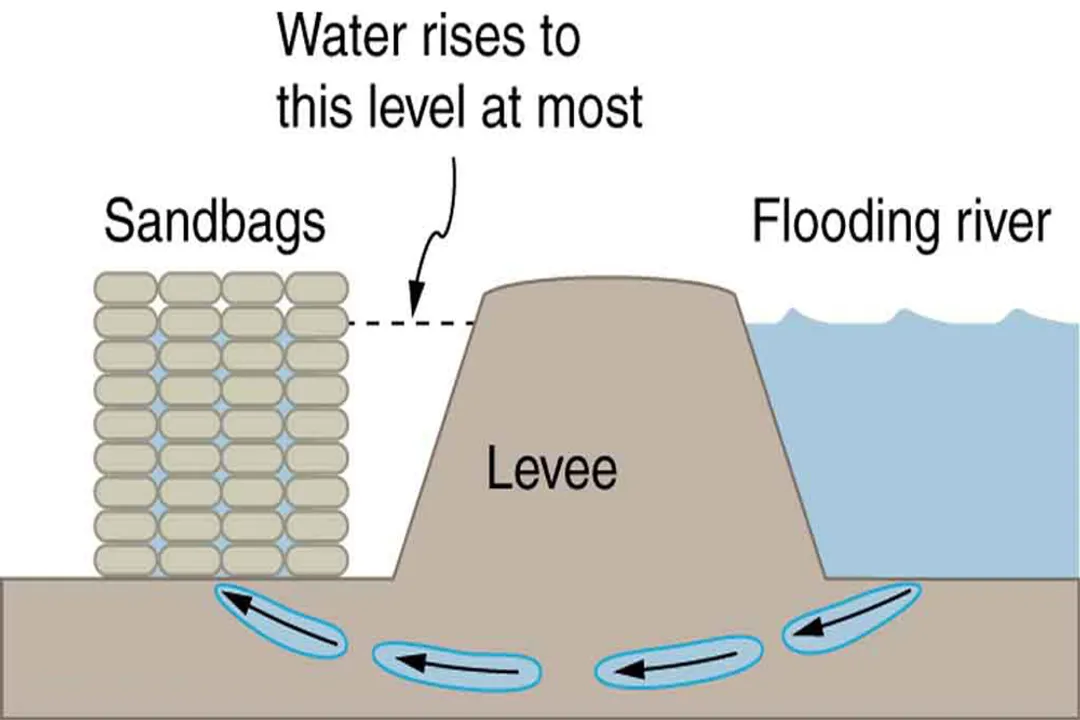
Understanding this depth-pressure relationship is not just an academic exercise; it dictates physical constraints in engineering and natural sciences. The rate of pressure increase is the critical parameter designers worry about when building structures for extreme environments.

For instance, consider the engineering constraint of a deep-sea submersible. The pressure increases by roughly $100$ kilopascals for every $10$ meters of water depth. ^[1] This means that descending $1,000$ meters subjects the hull to a crushing force equivalent to about $100$ times the pressure felt at the surface ($100$ atmospheres). ^[1] The $\rho g$ term dictates the severity of this challenge; if the ocean were filled with something half as dense as saltwater, the required hull strength for a given depth would be dramatically reduced, saving significant material and cost in construction. This direct proportionality between density and pressure increase is a constant factor that engineers must model accurately for safety. ^[4]

This concept also applies in reverse. When designing an aeration system for a large water reservoir, the required pump strength must overcome the hydrostatic pressure at the bottom. If the reservoir is $50$ meters deep, the pump must overcome $5$ atmospheres of pressure just to push water to the bottom exit, plus whatever additional pressure is needed for flow resistance throughout the piping system. Knowing that the pressure change is linear means that doubling the reservoir depth requires doubling the necessary additional pressure capacity from the pump, separate from the starting surface pressure. ^[8]

# Molecular View

If we zoom down to the microscopic level, the variation of pressure with depth is explained by the continuous, random motion and subsequent collisions of the fluid’s constituent particles (atoms or molecules). ^[2] Pressure arises because these particles exert forces on the surfaces they strike. ^[2]

In a fluid, the molecules are constantly moving and colliding with each other and with any container walls or submerged objects. When a fluid is under gravity, the molecules at greater depths are also constantly being bombarded from above by the molecules in the layer directly over them. ^[2][5] This continuous stream of molecules falling and transferring momentum downward creates the net downward force we measure as pressure. ^[5] The weight of the fluid above translates directly into an increased frequency and force of these molecular impacts at any lower point in the fluid structure. ^[2] It is the collective result of these countless, tiny collisions—governed by the mass of the particles (density) and the strength of the gravitational field—that results in the macroscopic hydrostatic pressure we observe. ^[5] This is why, in a zero-gravity environment, while molecules still collide, the overall hydrostatic pressure gradient with depth disappears because there is no weight to the fluid column. ^[5]

This understanding is crucial. It confirms that the pressure increase is not due to some mysterious property of the water itself compressing; it is purely a consequence of mass being subjected to gravity within a contained volume. ^[5][9] Even slight changes in temperature could subtly affect molecular kinetic energy, but the primary driver for the depth-dependent pressure change remains the steady, predictable weight of the fluid above. ^[2]