What is the great circle in a sphere?

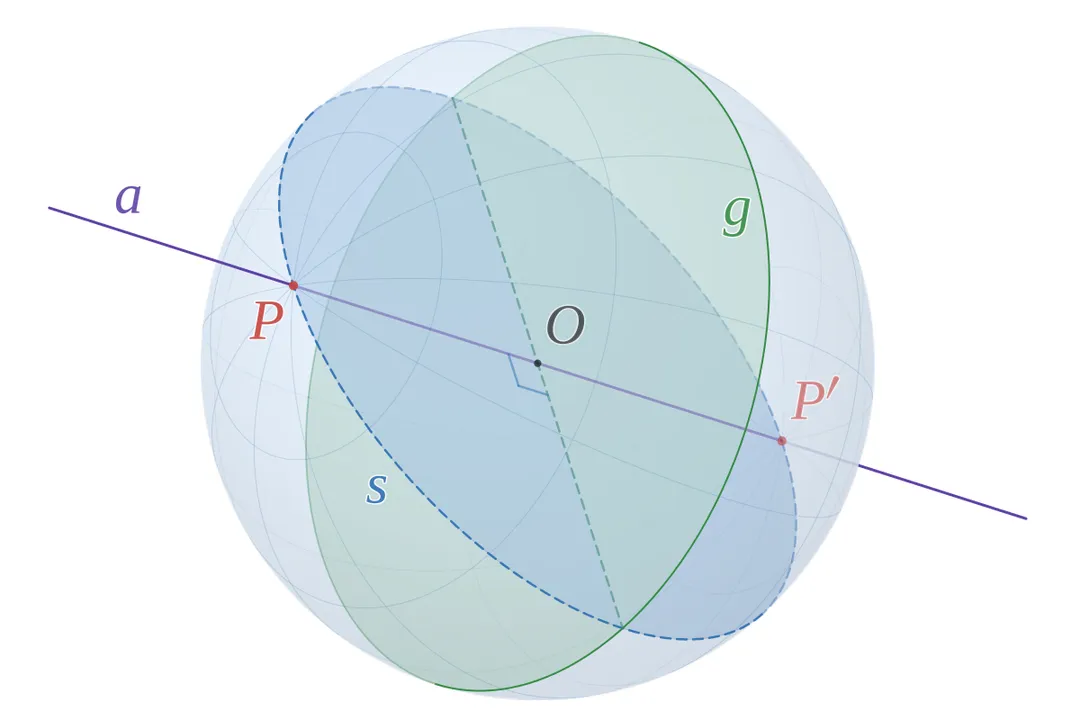
The largest possible circle one can draw on the surface of a sphere is known as a great circle. ^[1][2][6] This geometric feature is fundamental to understanding spherical geometry, navigation, and the structure of celestial bodies. ^[4][8] Conceptually, a great circle represents the intersection where a plane slices through the sphere, provided that the plane passes directly through the exact center of the sphere. ^[1][2]

The resulting circle shares the same center and the same radius as the sphere itself. ^[2] Because this cut is perfectly centered, the great circle divides the entire spherical surface into two equal halves. ^[1][6] These halves are naturally referred to as hemispheres. ^[1][6] If you imagine an orange; any cut that slices perfectly through the very middle of the fruit, passing through the core, creates a circular edge that defines a great circle on the peel's surface.

# Largest Circle

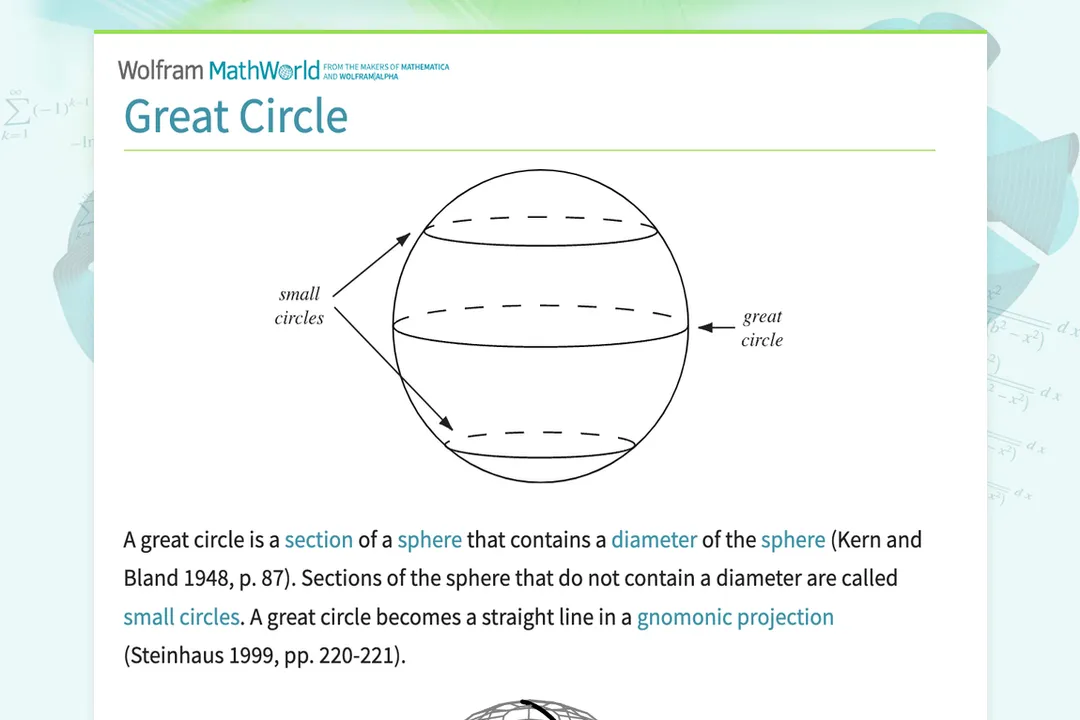
The primary characteristic distinguishing a great circle from any other circle drawn on a sphere is its size. ^[2] Any circle on a sphere whose plane does not pass through the center is called a small circle. ^[4] For instance, if you slice an orange parallel to its equator but closer to the top, the resulting circular cut is a small circle—it has a smaller radius than the orange itself and does not divide the orange into two equal halves. ^[4] This difference in radius is key: a great circle has a radius equal to the sphere's radius, while a small circle always has a radius smaller than the sphere's radius. ^[1][2]

This principle holds true whether we are considering a physical object like a ball or an abstract mathematical sphere existing in three-dimensional space. The size constraint imposed by requiring the intersecting plane to pass through the center is what grants the great circle its unique status. ^[8]

# Defining Points

The ability to define a unique great circle is closely tied to the selection of points on the sphere's surface. ^[3] If you pick any two distinct points on the sphere that are not directly opposite each other—meaning they are not antipodal—those two points will define exactly one unique great circle that passes through both of them. ^[3][6]

However, a specific condition alters this uniqueness. If the two chosen points are antipodal, meaning they are diametrically opposed on the sphere (like the North Pole and the South Pole), then an infinite number of great circles can be drawn that pass through both points. ^[3][6] Think of the Earth: the North Pole and South Pole are connected by every single line of longitude—each one represents a different great circle passing through both poles. ^[4] Similarly, three points on the surface of a sphere that do not all lie on the same small circle will uniquely define a single great circle. ^[3]

If you are trying to map out a route, knowing this geometrical rule is critical. For any two non-antipodal cities, there is only one shortest path along the surface defined by a specific great circle arc, which becomes the basis for efficient travel. ^[1][2] If you choose a path that is not the great circle, you are inherently taking a longer route. ^[9]

# Terrestrial Examples

When we look at our own planet, Earth, which is modeled very closely as a sphere for geographical purposes, the concept of the great circle becomes immediately applicable. ^[4] The most famous terrestrial great circle is the Equator. ^[1][8] It is the plane that cuts the Earth exactly in half along its middle, creating the Northern and Southern Hemispheres. ^[4]

Beyond the Equator, all lines of longitude, also known as meridians, are great circles. ^[1][4] These lines run from the North Pole to the South Pole. ^[8] Conversely, most lines of latitude, such as the Tropic of Cancer or the Arctic Circle, are small circles because they are parallel to the Equator and do not pass through the Earth’s center. ^[4] The only exception among the parallels is the Equator itself. ^[1]

This distinction is vital in mapping and navigation. If you were planning a journey that involved sailing due East or West, sticking strictly to a line of latitude (a small circle, unless you are on the Equator) would generally take you on a longer path than necessary, unless you were tracing the Equator itself. ^[9]

# Shortest Route

The most significant practical application of the great circle concept is in determining the shortest path between two locations on a spherical surface. ^[1][2] The arc of a great circle connecting two points represents the shortest possible distance between them along that surface, a path known in geometry as a geodesic. ^[9]

For anyone involved in long-distance aviation or maritime travel, understanding this is paramount for fuel efficiency and time savings. ^[9] When looking at a standard flat map, such as a Mercator projection, the flight path between distant cities often appears as a wide, curved arc over the map surface. ^[9] This visual curve can seem inefficient or circuitous. However, if you were to trace that same path onto a physical globe, you would see that the path is actually the straightest possible line between the two points—it lies along the segment of the great circle connecting them. ^[1][9] The apparent curve on the flat map is merely a distortion introduced by projecting the spherical surface onto a two-dimensional plane. ^[9] Pilots fly these great circle routes because they minimize the distance covered, even if the projection makes them look longer on a chart. ^[2]

Consider this practical analogy: if you are designing a fixed railroad track on a perfectly spherical world, the shortest way to connect two non-antipodal cities will always involve laying the track along the great circle arc between them. Any deviation from that arc, even a small amount to the "side," will increase the total length of the track required. ^[9]

# Geometric Definition

Mathematically, defining a great circle involves relating the geometry of the sphere to the geometry of planes in three-dimensional Cartesian space. ^[8] A sphere centered at the origin $(0, 0, 0)$ in three-dimensional space is described by the equation:

$$x^2 + y^2 + z^2 = R^2$$

where $R$ is the radius of the sphere. ^[8]

A plane that defines a great circle must pass through the origin. Such a plane is generally represented by the linear equation:

$$ax + by + cz = 0$$

where $a$, $b$, and $c$ are constants, and they cannot all be zero simultaneously. ^[8] The intersection of this plane with the sphere yields the great circle. The vector $(a, b, c)$ is the normal vector to the plane, meaning it points perpendicularly away from the plane's surface. For the plane to pass through the center of the sphere, its constant term must be zero, which is exactly what happens in the equation above. ^[8]

When you introduce specific coordinates for two points on the sphere, you can solve for the coefficients $a, b, c$ that satisfy the plane equation for both points simultaneously, thereby finding the unique plane—and thus the unique great circle—that connects them, assuming they aren't antipodal. ^[3] This mathematical underpinning confirms why the path is the absolute shortest available on the surface, as it adheres strictly to the simplest geometric slice possible through the sphere's volume. ^[1]